Конспект урока «Дифференцирование сложной функции» по математике
Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
на тему
«Дифференцирование сложной функции».
Выполнил:
преподаватель математики
первой квалификационной категории
Заварзина В.Г.
Липецк 2014 г.
Тема урока:
«Дифференцирование сложной функции».
Цели урока:
1. Образовательные:
а) закрепить навыки распознавания сложных функций и нахождения производных сложных функций;![]()
б) обобщить знания студентов о сложной функции и правиле нахождения производной сложной функции;
в) сформировать умения и навыки использования вычисления производной сложной функции для вычисления различных величин при решении прикладных задач и задач производственной направленности.
2. Развивающие:
а) развитие профессиональных качеств студентов (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а) воспитание навыков самостоятельной работы;
б) воспитание дисциплинированности;
в) воспитание эстетических взглядов.
Тип урока: комбинированный
Вид урока: проблемный
Методические приемы:
-самостоятельная работа (работа с раздаточным материалом);
-практический- решение задач производственной и прикладной направленности.
Межпредметные связи: история-электротехника-физика- производственное обучение.
Оборудование и наглядные средства обучения: мультимедийный проектор, интерактивная доска, презентация, демонстрационный и раздаточный материал, задачник “Алгебра и начала математического анализа” (профильный уровень часть 2) под редакцией А. Г. Мордковича .
Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока:
I.Организационный момент: Подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей)
II. Сообщение темы и целей урока.(слайд 1,2)
Эпиграф к уроку : “Просто знать - ещё не всё, знания нужно использовать” - Гёте (слайд 3)
Ш. Мотивация.
В наших домах, в транспорте, на заводах - всюду работает электрический ток.
Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
Сегодня на уроке мы применим ваши знания, касающиеся математики и электротехники при решении задач профессиональной направленности .
Задача.
(Преподавателем вводится задача, решение которой приводится в конце урока. )
Заряд, протекающий через проводник, меняется по закону ![]() .
.
Найти силу тока в момент времени t=5 cек. (слайд 4)
IV.Актуализация опорных знаний
Сегодня к уроку нужно было приготовить сообщение о Исааке Ньютоне и Г.В. Лейбнице.
Историческая справка (сообщение обучающегося) (слайд 5-6).
(Фотографии учёных)
(Ответ студента.)
Историческая справка.
Производная – одно из фундаментальных понятий математики.
Оно возникло в 18 веке. Независимо друг от друга И.Ньютон и
Г. Лейбниц разработали теорию дифференциального исчисления.
О Ньютоне.
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
А.Поуг.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.
Ньютоном были изучены все основные вопросы физики и математики, актуальные для его времени.
Ньютон, решая задачи на проведение касательных к кривым, вычисляя площади криволинейных фигур, создает общий метод решения таких задач – метод флюксий (производных). Ньютон вычислял производную и интеграл любой степенной функции. О дифференциальном и интегральном исчислениях ученый подробно пишет в своей самой значительной работе по математике «Метод флюксий» (1670-1671), которая была опубликована уже после его смерти. В ней были заложены основы математического анализа.
О Лейбнице
Готфрид Вильгельм Лейбниц. (1646-1716)
Работы Лейбница составляют фундамент математического анализа.
В основу новой науки он положил понятие дифференциала. Лейбниц дал правила вычисления производной суммы, разности, произведения, дроби.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.
Но это не говорит о том, что до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.
Используя методы дифференциального исчисления, учёные предсказали возвращение кометы Галлея, что было большим триумфом наукиXVIII века.
Необходимо сказать, что Ньютон не дал четкого определения производной. Впервые определение производной было сформулировано французским математиком О.Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа)
Повторение пройденного материала:
-
Что называется дифференцированием сложной функции?
Студент: Производная сложной функции равна ![]() произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной
произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной
-
Назовите формулы для производных элементарных функций.
Студент:
1.![]()
2.![]()
3.![]()
4.![]()
![]()
5. ![]()
6.![]()
7.![]()
-
Назовите формулы для производных тригонометрических функций.
Студент:
1.![]()
2. ![]()
3.![]()
4. ![]()
-
Назовите правила вычисления производных (слайд 7).
Студент:
Основные правила дифференцирования
Пусть ![]() , тогда:
, тогда:
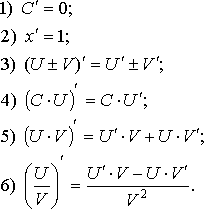
-
Какая функция является сложной?
(Студент: функции от функций называют сложными функциями.
Пусть функция u=g(x) определена на множестве X и U – множество значений этой функции. Пусть, множество U является областью определения функции y=f(u). Поставим в соответствие каждому x из X число f(g(x)) . Тем самым на множестве X будет задана функция y=f(g(x)). Ее называют композицией функций или сложной функцией.)
-
Назовите формулу нахождения производной сложной функции.
(слайд 8)
Студент: ![]() =
= ![]()
--правило дифференцирования сложной функции.
7. Перед Вами несколько функций.( слайд 9)
Давайте назовём из каких функций состоят следующие функции и найдём их производные.
a) f(x)= tg3x
Решение:![]()
б) y=![]()
Решение:![]()
в) y=![]()
Решение: ![]()
г) f(x)=![]()
Решение:![]()
д) f(t)=sin(2t+![]() )
)
Решение:![]()
8. Теперь перейдем к самостоятельной работе.
Самостоятельная работа.(слайд 10 название)
| II Вариант | |
| Найдите производные функций: | Найдите производные функций: |
| 1) y=cos7x | 1) y=sin10x |
| 2) y= | 2) y= |
| 3) y= | 3) y= |
| 4) y=3sinx+ | 4) y= |
| 5) y= | 5) y = |
Решение примеров из самостоятельной работы.
I Вариант
1) y=cos7x
Решение:
![]()
2) y=![]()
Решение:
![]()
3) y=![]()
Решение:
![]()
![]()
4) y=3sinx+ ![]()
Решение:
![]()
5) y=![]()
Решение:
![]()
II Вариант
1) y=sin10x
Решение:
![]()
2) y=![]()
Решение:
![]()
3) y=![]()
Решение:
![]()
4) y=![]() +4cosx
+4cosx
Решение:
![]()
5) y =![]()
Решение:
![]()
V. Решение задач.
Вернёмся к теме нашего сегодняшнего урока.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д., так как механический смысл производной это ![]() .
.
Мощным средством в математике, физике, механике, электротехнике и других дисциплинах является производная сложной функции – одно из основных понятий математического анализа.
У Вас на столах лежит таблица для нахождения производных физических, электротехнических и математических величин. (слайд11).
Производные функций нашли широкое применение при решении прикладных задач на нахождение силы, мгновенной скорости, силы тока, теплоёмкости и других величин.
1. Сила-- есть производная работы по перемещению.
2.Сила тока I-- есть производная заряда q по времени.
3.Мгновенная скорость– есть производная пути по времени .
4. Теплоемкость – есть производная теплоты по температуре, т.е. C(t) =Q/(t)
| Вычисление производной | |
| А – работа; F – сила; N - мощность. | F(x)=A' (x); N(t)=A' (t). |
| Q –электрический заряд; I – сила тока. | I(t)=q' (t) |
| S –перемещение; v –скорость. | V(t)=S' (t) |
| Q –количество теплоты; с – теплоёмкость. | C(t)=Q' (t) |
Давайте с помощью перемещения найдём скорость изменения тока, идущего по проводнику.
Давайте запишем в тетради следующую задачу.
Задача 1.(слайд 12).
Найдите скорость изменения тока, идущего по проводнику, по закону i=2sin(3t + ![]() )
)![]() в момент времени t=
в момент времени t=![]() .
.
Решение: т.к. скорость есть производная от пути по времени ![]()
![]() , то скорость изменения тока, идущего по проводнику будем находить, как производную от i.
, то скорость изменения тока, идущего по проводнику будем находить, как производную от i.
Т.к. i=2sin(3t + ![]() )
)![]() -- сложная функция, то
-- сложная функция, то
![]()
Находим значение производной в момент времени t=![]()
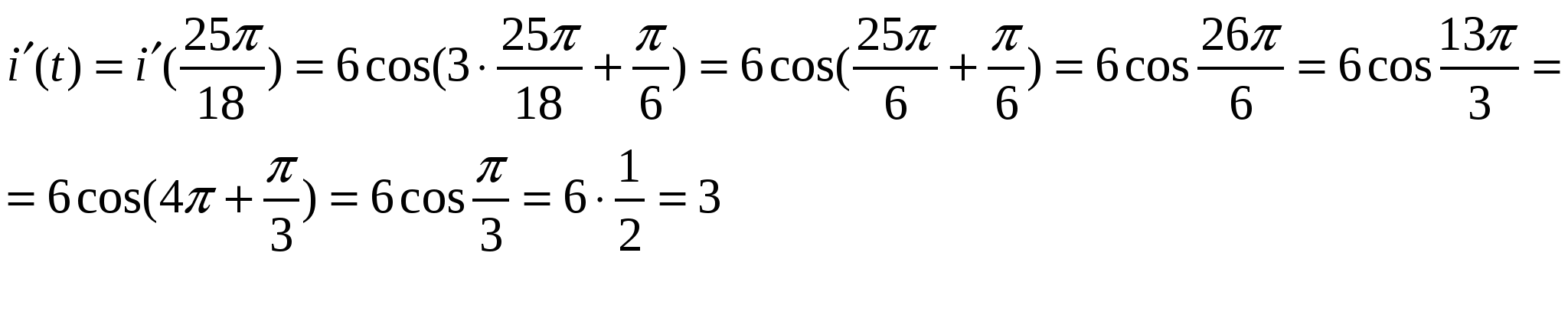
VI. Закрепление пройденного материала.
Рассмотрим задачу урока.
Задача 2 (слайд 13).
Заряд, протекающий через проводник, меняется по закону ![]() .
.
Найти силу тока в момент времени t=5 cек.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
![]()
Решение: найдём производную заряда, как производную сложной функции:
![]()
Мы нашли силу тока I=2cos(2t-10)
Найдём силу тока в момент времени t=5 cек.
I(5)=2cos(![]() )=2cos0=2*1=2
)=2cos0=2*1=2
VII.Подведение итогов урока:
Сегодня на уроке мы повторили правила вычисления производных, дифференцирование сложной функции, формулы для вычисления производных, решили задачи на нахождение физических величин, самостоятельно решали задачи на нахождение производных.
Выставление оценок за урок.
VIII.Домашнее задание:
Составить и решить задачу на нахождение силы тока , № 42.2(а-г) из учебника на стр.233. (слайд 14).
Список литературы:
1. Дидактические материалы по алгебре и началам анализа для 10 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.
4. Алгебра и начала анализа: Учеб. для 10 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2003.
5 Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
Здесь представлен конспект к уроку на тему «Дифференцирование сложной функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

