Конспект урока «Критические точки функции, максимумы и минимумы» по математике
Тема: «Критические точки функции, максимумы и минимумы»
Знать: определения точек максимума и минимума функции; необходимое и достаточное условие существования экстремума, алгоритм исследования функции на экстремум.
Уметь: определять критические точки, находить экстремумы функции.
Тип урока: комбинированный.
Цели урока:
-
Образовательная - уметь определять критические точки функции, максимумы и минимумы функции».
2. Развивающая - развитие у учащихся логического мышления, умения анализировать
и обобщать изученный материал, применять знания теории к практике.
3. Воспитательная - развивать чувства ответственности, взаимопомощи
Ход урока.
1.Орг. момент.
2.Математический диктант:
| Вопросы | Ответы | |
| 1 | Соответствие с областью определения Д, при котором каждому числу х, из множества Д сопоставляется по некоторому правилу число у, зависящее от х, называется… |
|
| 2 | Множество всех возможных значений х, называется… |
|
| 3 | Разность между новым значением аргумента и первоначальным значением аргумента, называется… |
|
| 4 | Разность между новым значением функции и первоначальным значением функции, называется… |
|
| 5 | Предел отношении приращения функции к приращению аргумента, когда приращение аргумента стремится к 0, называется… |
|
| 6 | Дифференцирование - … |
|
| 7 | Правила вычисления производных: … |
|
| 8 | Если f‘′(x)>0 в каждой точке интервала I, то функция f … на I. |
|
| 9 | Если f‘ (x)I, то функция f … на I. |
|
№279
б) f(x) = -x3 + 2x-3. D(f)=R f ‘(x) = -2x + 2;
-2x + 2 = 0; x =1;
 f(x) убывает на
f(x) убывает на ![]() f ‘ + -
f ‘ + -

 f(x) возрастает на
f(x) возрастает на ![]() x
x
f 1
г) f(x) = 5x2-3x + 1. D(f) = R f ‘(x ) = 10x – 3;
10x – 3 = 0; x = 0,3.
f( x) убывает на ![]() ;
;
 f( x) возрастает на
f( x) возрастает на ![]() . f ‘ - +
. f ‘ - +

 f(x) возрастает на
f(x) возрастает на ![]() x
x
f 0.3
№ 280
б) f( x) = х2 ∙ (х - 3) = x3 - 3 х2; D(f) = R; f′(x )= 3 х2 - 6х;
3 х2 - 6х = 0; 3х(х – 2) = 0; х1 = 0; х2 = 0.
f( x) возрастает на ![]()
![]()
![]()
f( x) убывает на ![]() f ‘ + - +
f ‘ + - +




 f(x) возрастает на
f(x) возрастает на ![]() | | x
| | x
f 








 0 2
0 2
f ‘ + - +
г ) f( x) = x3 – 27х ; D(f) = R; f′(x) = 3 х2 – 27 | |
) f( x) = x3 – 27х ; D(f) = R; f′(x) = 3 х2 – 27 | |


 3 х2 – 27 = 0; f -3 3 x
3 х2 – 27 = 0; f -3 3 x
х2 = 9;
х1/2 = ± 3; f( x) возрастает на ![]()
![]()
![]()
f( x) убывает на ![]()
№ 283
f ‘ + - +
а ) f( x) = x3 + 3х2 – 9х + 1; D(f) = R; | |
) f( x) = x3 + 3х2 – 9х + 1; D(f) = R; | |



 f′(x) = 3х2 + 6х – 9; f -3 1 X
f′(x) = 3х2 + 6х – 9; f -3 1 X
3х2 + 6х – 9 = 0;
х2 + 2х – 3 = 0; х1 = -3; х2 = 1;
f( -3) = -27 + 27 + 27 + 1 = 28;
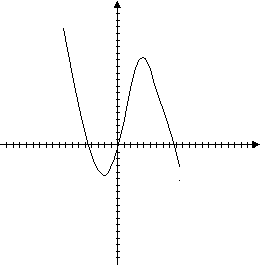 f( 1) = 1 + 3 – 9 + 1 = -4;
f( 1) = 1 + 3 – 9 + 1 = -4;
 f( 0) = 1;
f( 0) = 1;
а) в)
f ‘ - + -
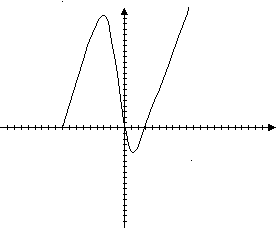
в ) f( x) = 2 + 9х + 3х2 - x3; D(f)=R; | |
) f( x) = 2 + 9х + 3х2 - x3; D(f)=R; | |


 f′(x) = 9 + 6х - 3х2 = -3(х – 3)(х + 1) f -1 3 x
f′(x) = 9 + 6х - 3х2 = -3(х – 3)(х + 1) f -1 3 x
-3(х – 3)(х + 1) = 0;
х1 = 3; х2 = -1;
f( -1) = 2 – 9 + 3 + 1 = -3
f( 3) = 2 + 27 + 27 – 29 = 29;
f( 0) = 2;
3. Новая тема.
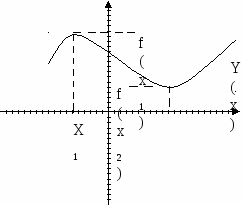
у
Y=f(x)
f (x1)
f (x2)
х
X1 X2
Точка х0 из области определения функции f( x) называется точкой максимума (минимума) этой функции, если существует такая окрестность этой точки, что для всех
х ≠ х0 из указанной окрестности выполняется неравенство f′(x) f( х0) (f′(x) > f( х0) ) .
значение функции в точке максимума(минимума) называется максимумом (минимумом) этой функции: тах f′(x)= f( x0) (тіп f( x) = f( x0) ). Точки максимума(минимума) функции называются её точками экстремума, а максимум и минимум функции – экстремумом этой функции. Для функции у = f( x), изображенной на рисунке:
х1 – точка максимума; тах f′(x)= f( x1);
х2 – точка минимума; тіп f( x) = f( x2).
При нахождении экстремума функции используется теорема Ферма (необходимый признак экстремума). Если х0 – точка экстремума функции у = f( x) то производная в этой точке равна 0, т.е. f′(x0) = 0, или не существует.
Определение:
Точки, в которой f′(x) = 0 или f′(x) не существует, называются критическими.
Однако не всякая критическая точка является точкой экстремума. Чтобы определить, является ли критическая точка точкой экстремума, используется достаточный признак экстремума.
Если при переходе (слева направо) через критическую точку (в которой функция определена) производная меняет знак с «+» на «-», то эта точка является точкой максимума, с «-» на «+» то точкой минимума данной функции. Если при переходе через критическую точку производная знака не меняет, то эта точка не является точкой экстремума рассматриваемой функции
Пример 1. Исследовать на экстремум функцию.
у = x3 – 3х. D(у) = R; у′ = 3 х2 – 3 = 3 ∙ (х2 -1 ); f ‘ + - +
3 ∙ (х2 -1 ) = 0; | |
∙ (х2 -1 ) = 0; | |
х

 2 - 1 = 0; f -1 1 x
2 - 1 = 0; f -1 1 x
х1/2 = ±1; f′(-2) = 3 ∙ (-2)2 -3 = 9 > 0;
f′(0) =-1
f′(2) = 3 ∙ 22 – 3 = 9 > 0;
Вопрос:
Как ведёт себя производная на данных промежутках?
Дети делают вывод:
При переходе через точку 1 производная изменила знак с «-» на «+» , поэтому эта точка является точкой минимума; х тіп = 1, у тіп= 1 – 3 = -2.
При переходе через точку -1 производная изменила знак с «+» на «-» , поэтому эта точка является точкой максимума; х тах = -1, у тах= -1 + 3 = 2.
Ответ: А тах (-1;2)
В тіп (1;-2)
Пример 2. Исследовать функцию на возрастания и убывания , экстремумы. Постройте график функции:
у = х3 – 3х2 + 1.
D(f) = R у′ = 3х2 – 6х = 3х(х - 2). f ‘ + - +
 3х(х - 2) = 0 | |
3х(х - 2) = 0 | |


 х1 = 0; х2 = 2. f 0 2 x
х1 = 0; х2 = 2. f 0 2 x
f′′(-1) = 3 ∙ (-1)2 – 6 ∙ (-1) = 3 + 6 = 9 > 0.
f′′(1) = 3 – 6 = -3
f′′(3) = 3 ∙ 9 – 18 = 9 > 0
х тіп = 2, у тіп= -3
х тах= 0, у тах= 1
Ответ: А тах (0;1)
В тіп (2;-3), f( x) возрастает на ![]()
![]()
![]()
f( x) убывает на ![]()
4.Работа по карточкам.
а) f( x) возрастает на ![]()
![]()
![]() А тах (-5;5)
А тах (-5;5)
f( x) убывает на ![]()
![]()
![]() В тах(5;3)
В тах(5;3)
С тіп (1;-3)
б) f( x) возрастает на ![]()
![]()
![]() А тах (-4;3)
А тах (-4;3)
f( x) убывает на ![]()
![]()
![]() В тах(4;5)
В тах(4;5)
С тіп (-2;-2)
в f( x) возрастает на ![]() А тах (3;2)
А тах (3;2)
f( x) убывает на ![]()
![]()
![]() В тіп (-3;-2)
В тіп (-3;-2)
г) f( x) возрастает на ![]()
![]()
![]()
![]()
![]() А тах (-2;3)
А тах (-2;3)
f( x) убывает на ![]()
![]()
![]()
![]()
![]() В тах(2;3)
В тах(2;3)
С тіп (-4;-2)
Д тіп (4;-2)
5.Закрепление темы.
№ 288
а) f( x) = 4 – 2х + 7х2 , D(f)=R; f′( x) = -2 + 14х;
-2 + 14х = 0
х = ![]() ;
;
г) f( x) = 4х – ![]() , D(f)=R; f′( x) = 4 – х2
, D(f)=R; f′( x) = 4 – х2
4 – х2 = 0
х1 = -2, х2 = 2.
Ответ: а) х = ![]() ; г) х1 = -2, х2 = 2.
; г) х1 = -2, х2 = 2.
№ 290
а) f( x) = 5 + 12х – х3; D(f)=R; f′( х) = 12 – 3х2;
12 – 3х2 = 0;
3х2 = 12;
- | + | -



 х1 = -2, х2 = 2; -2 2 x
х1 = -2, х2 = 2; -2 2 x
f′( -3) = -15 f′( 0) = 12 > 0, тіп тах
f′( 3) = -15
х тіп = -2, х тах= 2,.
б) f( x) = 9 + 8х2 – х4; D(f)=R;
f′( 1) = 16х – 4х3; + - + -
 16х – 4х3 = 0; 4х ∙ (4 – х2) = 0; | | | x
16х – 4х3 = 0; 4х ∙ (4 – х2) = 0; | | | x



 х1 = 0; х2 = -2; х3 = 2. -2 0 2
х1 = 0; х2 = -2; х3 = 2. -2 0 2
х тах = -2;2,. тах тіп тах
х тіп = 0,.
Дана функция:
-
f( x) = 6х -2х3 + 1;
-
f( x) = х3 – 12х – 1;
Найти область определения, производную, критические точки, промежутки возрастания и убывания, экстремумы функции и построить график.
1. f( x) = 6х -2х3 + 1; D(y) = R f′( x) = 6 – 6x2. 6 – 6x2 = 0. x2 = 1. x1/2 = ± 1.
- + -
 | | x
| | x


 -1 1 f( 0) = 1
-1 1 f( 0) = 1
тіп тах (-∞;-1] ![]() [1;+∞) убывает; [-1;1] возрастает
[1;+∞) убывает; [-1;1] возрастает
Атах (1;5)
Втіп (-1;-3)
-
f( x) = х3 – 12х – 1; D(y) = R f′( x) = 3х2 – 12, 3х2 – 12 = 0, x2 = 4. x1/2 = ± 2
+ - +
 | | x
| | x
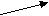
 -2 2
-2 2
тах тіп
f( 0) = -1;
(-∞;-2] ![]() [2;+∞) возрастает; [-2;2] убывает
[2;+∞) возрастает; [-2;2] убывает
Атах (-215)
Втіп (2;-17)
6.Тест по теории .
Вариант 1
1.Если функция f(x) непрерывна на интервале (а; b) и f′(x) > 0 для всех
х ![]() (а; b), то функция _________________________ на интервале (а; b).
(а; b), то функция _________________________ на интервале (а; b).
2. Если функция f(x) непрерывна на интервале (а; b) и f′(x) __ 0 для всех
х ![]() (а; b), то функция возрастает на интервале (а; b).
(а; b), то функция возрастает на интервале (а; b).
3.Пусть функция f(x) непрерывна на интервале (а; b), и х0![]() (а; b), и f′(x0) = 0. Тогда если при переходе через локальную точку х0 функции f(x), её производная меняет знак с «+» на «-», то точка х0 – точка ___________________ функция f(x).
(а; b), и f′(x0) = 0. Тогда если при переходе через локальную точку х0 функции f(x), её производная меняет знак с «+» на «-», то точка х0 – точка ___________________ функция f(x).
4. Если функция f(x) непрерывна в точке х0 и производная в этой точке меняет знак с «__» на «__», то х0 - точка минимума.
5.Если х0 – точка экстремума функции у = f(x), то производная в этой точке равна ______ .
Вариант 2
1. Если функция f(x) непрерывна на интервале (а; b) и f′(x)___ 0 для всех
х ![]() (а; b), то функция убывает на интервале (а; b).
(а; b), то функция убывает на интервале (а; b).
2. Если функция f(x) непрерывна на интервале (а; b) и f′(x)
х ![]() (а; b), то функция ______________ на интервале (а; b).
(а; b), то функция ______________ на интервале (а; b).
3. Пусть функция f(x) непрерывна на интервале (а; b), и х0![]() (а; b), и
(а; b), и
f′(x0) = 0. Тогда если при переходе через локальную точку х0 функции f(x), её производная меняет знак с «-» на «+», то точка х0 – точка ___________________ функция f(x).
4. Если функция f(x) непрерывна в точке х0 и производная в этой точке меняет знак с «__» на «__», то х0 - точка максимума.
5. Точки, в которых производная функции равна 0, называются _______________ .
7. Дополнительное задание.
№ 294
Постройте эскиз графика функции обладающей следующими свойствами:
А) D(f)=![]() , f′( х) > 0, при х € (-3;1), f′( х) f′( 1) = 0.
, f′( х) > 0, при х € (-3;1), f′( х) f′( 1) = 0.
Б) D(f)= ![]() , f′( х) f′( х) > 0, при х € (1;5); функция f не имеет производной в точке 1.
, f′( х) f′( х) > 0, при х € (1;5); функция f не имеет производной в точке 1.
8. Контрольные вопросы.
Какую точку называют критической точкой функции?
Сформулируйте признак максимума(минимума) функции?
9. Задание на дом.
-
№ 288 (б,в)
-
№ 293 (а,в)
-
№ 295 (а,в)
-
Реферат на тему:«Пьер Ферма»
10. Итог урока.
Здесь представлен конспект к уроку на тему «Критические точки функции, максимумы и минимумы», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

