Конспект урока «Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции» по математике
Министерство образования и науки Самарской области
ГБОУ СПО «Безенчукский аграрный техникум»
Конспект занятия.
ТЕМА. Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции.
Цель: Формирование математических компетенций студентов посредством возможностей информационно-коммуникационной среды.
Задачи:
Образовательная: в ходе изучения данной темы студент должен:
знать: определение предела функции в точке; свойства предела функции в точке; определение непрерывности функции в точке; свойства непрерывных функций;
уметь: вычислять несложные пределы функций в точке и на бесконечности.
Воспитательная: прививать интерес к математике на основе исторического материала, формировать умение работать в группе, нести ответственность за результат выполнения заданий.
Развивающая: развивать логическое мышление, внимание, умение видеть проблему, находить пути её решения, переносить знания на новую ситуацию.
Тип урока: изучение нового материала.
Формы и методы: словесный, наглядный, фронтальная работа, самостоятельная групповая работа студентов.
Обеспечение: учебники: А. Дадаян «Математика» §5.11,§5.12,
Н.Богомолов «Математика» §42,
мультимедийная установка для демонстрации слайдов, бумага, фломастеры, карандаши, линейки, магниты.
Раздаточный материал: опорные конспекты, решение типовых примеров.
Время: 90 минут.
Структура занятия.
-
Организационный момент. Постановка цели и задач урока. Мотивация.
-
Актуализация знаний.
-
Изучение нового материала.
-
Решение типовых задач.
-
Самостоятельная работа студентов в группах.
-
Домашнее задание.
-
Рефлексия. Итоги занятия.
Ход занятия.
1.Организационный момент. Продолжительность работы-10 минут
Приветствие, оформление журнала. Объявление темы урока «Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции».
Постановка цели и задач урока:
Изучить определение и свойства предела функции в точке;
определение непрерывности функции в точке;
свойства непрерывных функций;
научиться вычислять несложные пределы функций в точке и на бесконечности
Мотивация. Продолжительность работы-2 минуты
Одновременно с развитием понятия функции развивалось и понятие предела функции. Первоначально ввести понятие предела функции пытался И.Ньютон, но только в 19 веке в работах А. Вейерштрасса, Б. Больцано, О. Коши сложились определение и обозначения пределов функции, используемые и в настоящее время. Понятие предел функции в точке лежит в основе понятия производной.
Понятие непрерывности играет важную роль, т.к. многие физические процессы характеризуются тем, что плавное изменение физических величин сменяется скачкообразным. Т.е. количественные изменения переходят в качественные.
Это один из основных законов диалектики.
-
Актуализация знаний. Продолжительность работы-3 минуты
Задание. 1) сформулировать определение функции
2) найти область определения функции (работа студентов у доски –
3 человека, с последующей проверкой. Запись сделать заранее.):
а) f(x) = x2+x-1; б) f(x) =![]() ; с)f(x) =
; с)f(x) =![]() .
.
-
Изучение нового материала ( сопровождается демонстрацией слайдов). Продолжительность работы-15 минут
3.1.Определение предела функции в точке.
Сформулируем определение предела функции в точке.
Определение. Пусть функция ![]() определена в некоторой окрестности точки а, кроме, может быть, самой точки а.
определена в некоторой окрестности точки а, кроме, может быть, самой точки а.
Число В называется пределом функции ![]() в точке а (или при
в точке а (или при ![]() ), если для любой последовательности значений аргумента
), если для любой последовательности значений аргумента ![]() , последовательность соответствующих значений функции, сходится к числу В.
, последовательность соответствующих значений функции, сходится к числу В.
Это же определение предела функции в точке часто рассматривают в другой формулировке:
О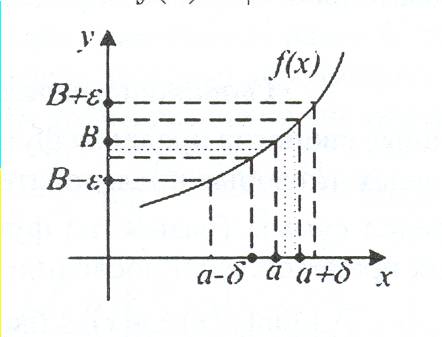 пределение. Постоянная В называется пределом функции
пределение. Постоянная В называется пределом функции ![]() при
при ![]() (или в точке а), если для любого числа
(или в точке а), если для любого числа ![]() существует такое число
существует такое число ![]() , что при всех х, удовлетворяющих условию:
, что при всех х, удовлетворяющих условию:
![]() ,
,
выполняется неравенство: ![]() .
.
Понятие предела возникает при определенном типе движения «по графику функции» - когда аргумент приближается к а, значение функции приближается к В.
Оба определения эквивалентны.
В этом случае пишут: ![]()
3.2.Свойства пределов функций
Основные свойства пределов функций:
-
Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:
![]()
-
Предел произведения функций равен произведению их пределов, если последние существуют:
![]()
Следствие. Постоянный множитель можно выносить за знак предела: ![]() , если предел
, если предел ![]() существует.
существует.
-
Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
 , если
, если ![]() .
.
Пример. Вычислить пределы:1. ![]() , 2.
, 2. ![]() , 3.
, 3.![]()
Решение.1. ![]() ;
;
-
Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель и знаменатель на множители:
![]()
3. ![]()
Ответ: 1)11; 2) -1; 3) 2
3.3 Изучение нового материала. Самостоятельная работа студентов в группах. Продолжительность работы-25 минут.
Цель. Проработать информацию, вычленить существенное, главное.
Составить опорный конспект- плакат и представить его.
Преподаватель выдает карточки с заданием каждой группе;
наблюдает, направляет, консультирует.
Задание 1 группе. Изучить §42(Н.В. Богомолов) Бесконечно большие функции. Определение, свойства. Оформить опорный конспект- плакат, сделать презентацию.
Задание 2 группе . Изучить §42 (Н.В. Богомолов) Бесконечно малые функции. Определение, свойства. Оформить опорный конспект- плакат, сделать презентацию.
Задание 3 группе. Изучить § 42 (Н.В. Богомолов) Связь между бесконечно малой и бесконечно большой функциями. Оформить опорный конспект- плакат, сделать презентацию.
Задание 4 группе. Изучить §5.14(А.А.Дадаян, §44 Н.В. Богомолов) Непрерывность функции в точке, на интервале. Определение, свойства, примеры. Оформить опорный конспект- плакат, сделать презентацию.
Преподаватель подводит итоги этапа.
3.4 Решение типовых примеров. (Устно). Слайды
Цель: разобрать решение типовых задач. Продолжительность работы-12 минут.
ПРАВИЛО 1. Чтобы раскрыть неопределенность вида ![]() , надо числитель и знаменатель дроби разложить на множители с последующим сокращением.
, надо числитель и знаменатель дроби разложить на множители с последующим сокращением.
ПРИМЕР 1.Вычислить: ![]()
Решение. ![]() .(проблема!)
.(проблема!)
1) 2х2+х-10=0 2) х2+х-6=0
D=b2-4ac D=1-4∙(-6)=25
D=1-4∙2(-10)=81 ![]()
![]() x2+x-6=(x-2)(x+3)
x2+x-6=(x-2)(x+3)
2x2+x-10=2(x-2)(x+![]() )=(x-2)(2x+5)
)=(x-2)(2x+5)
Заметим, что х 2, но не равен 2, следовательно, множитель, на который сокращаем (х-2), отличен от нуля при х2
ПРАВИЛО 2: Чтобы раскрыть неопределенность вида ![]() , надо числитель и знаменатель дроби разделить на старшую степень неизвестного.
, надо числитель и знаменатель дроби разделить на старшую степень неизвестного.
ПРИМЕР 2. ![]()
Решение: 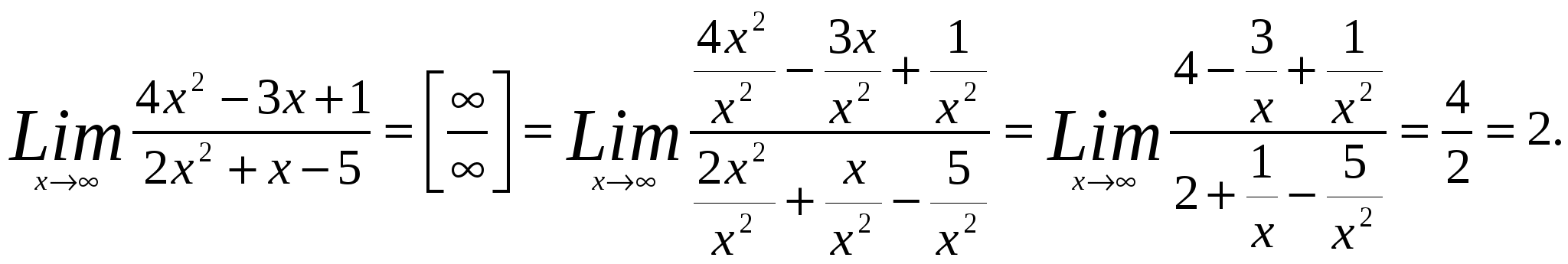
5. Решение примеров. Самостоятельная работа студентов в группах.
Цель: решение примеров, первичное закрепление.
Задание выдается на карточках. Продолжительность работы-15 минут
Найти пределы:
-
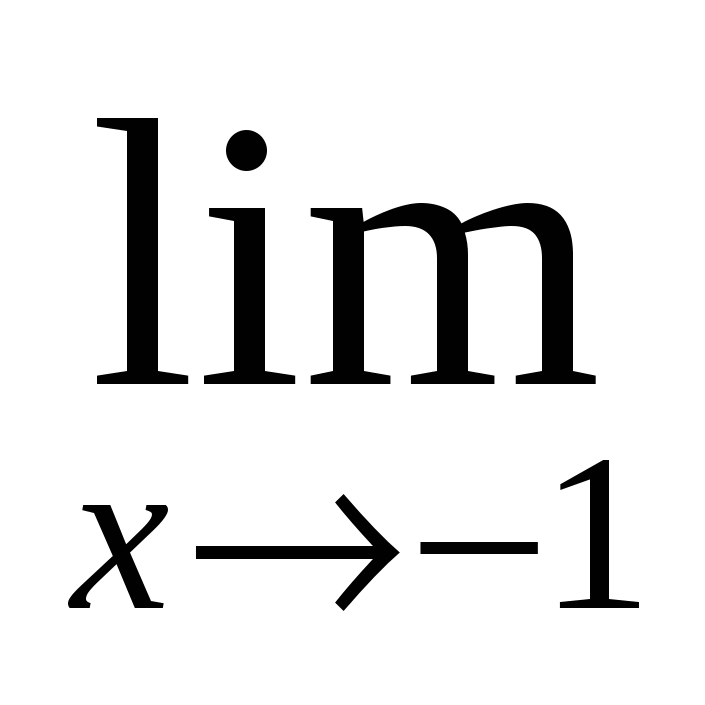 (x4-3x2+16x+1)
(x4-3x2+16x+1) -
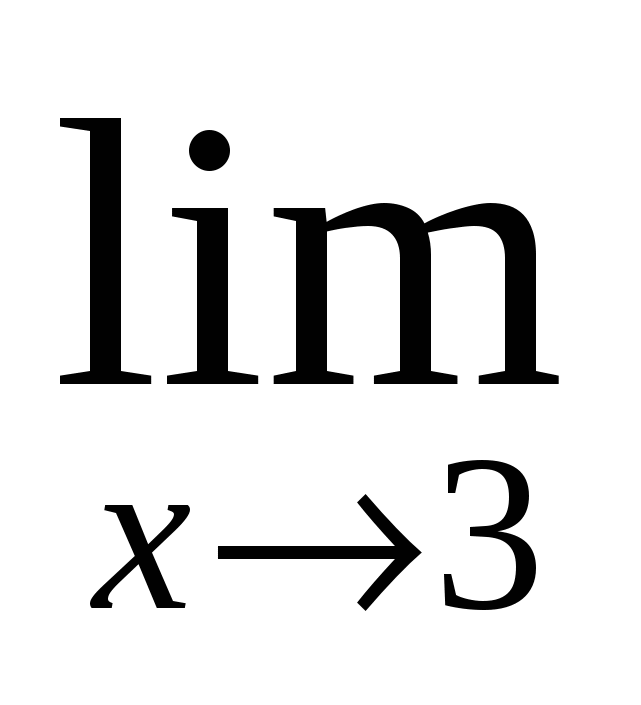
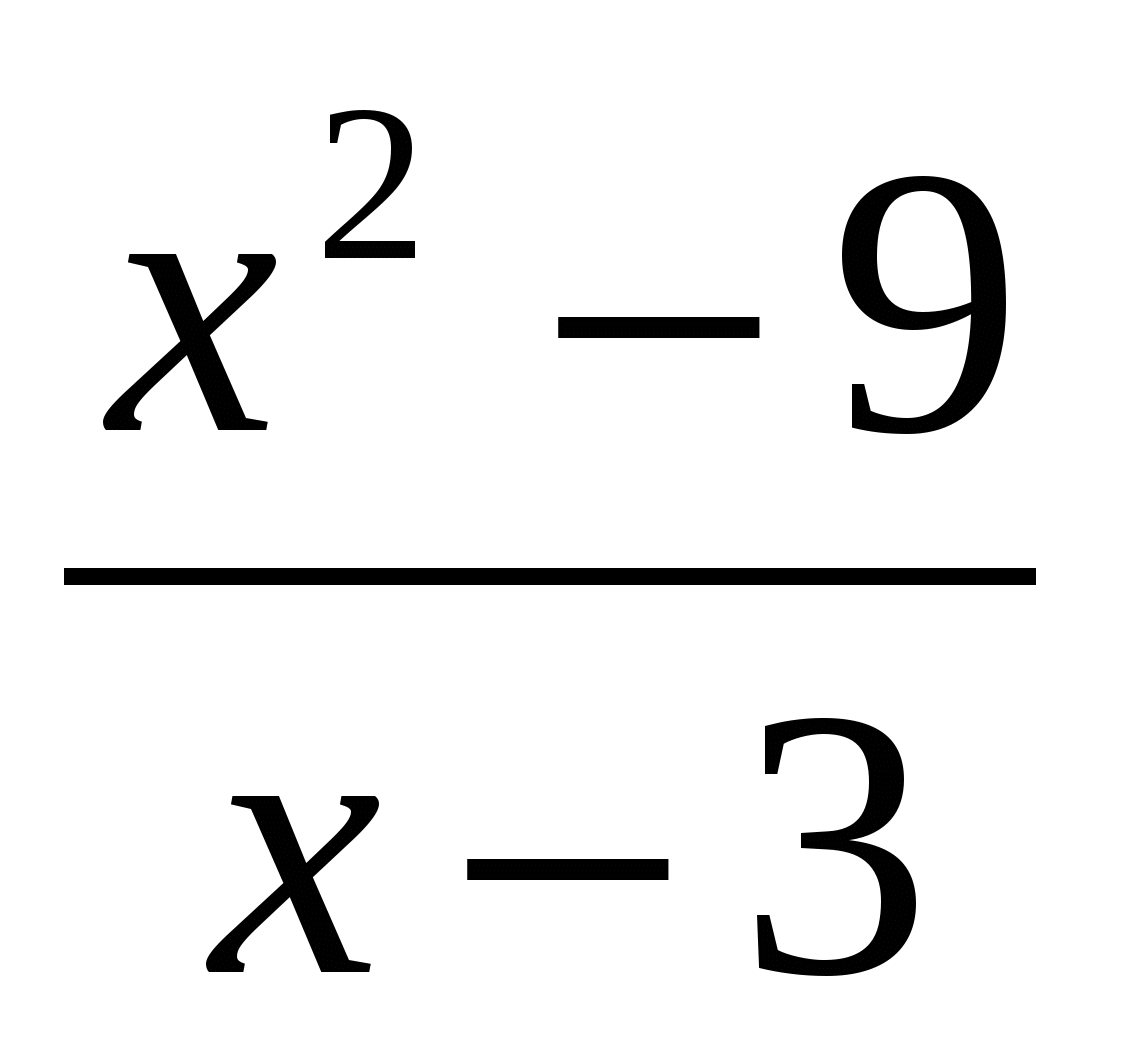
-
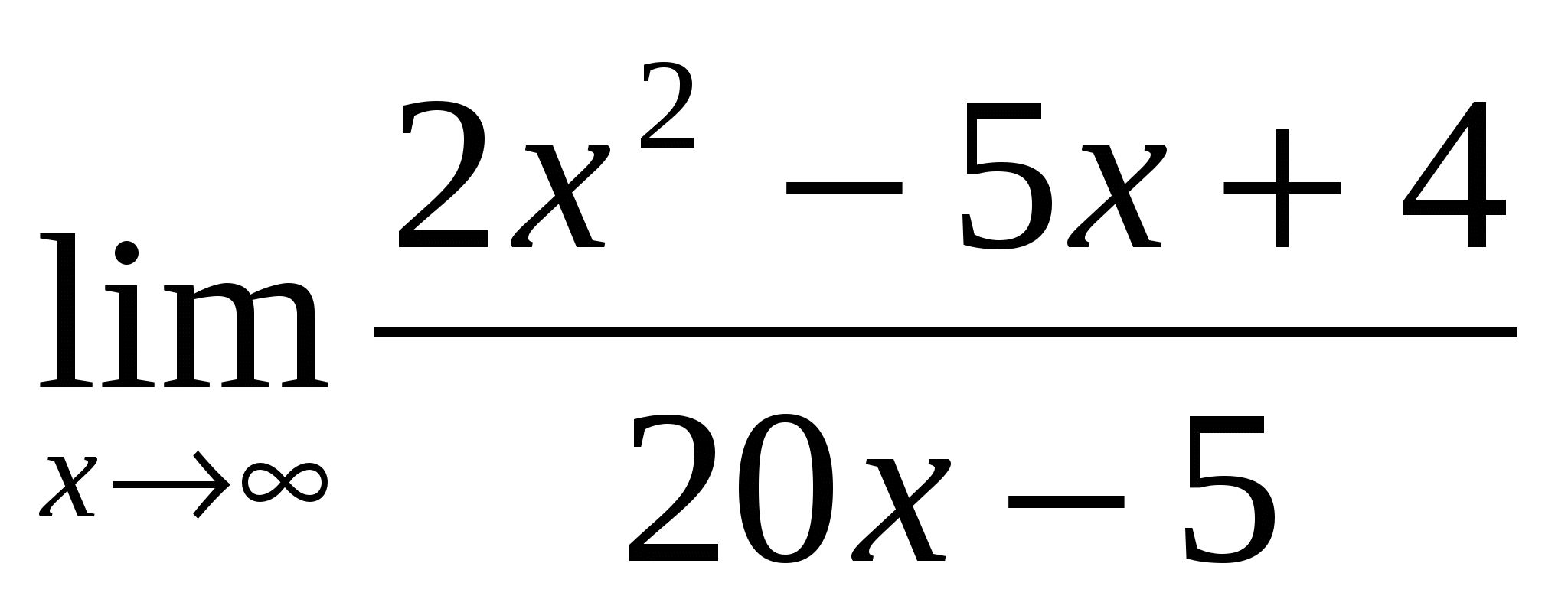
-
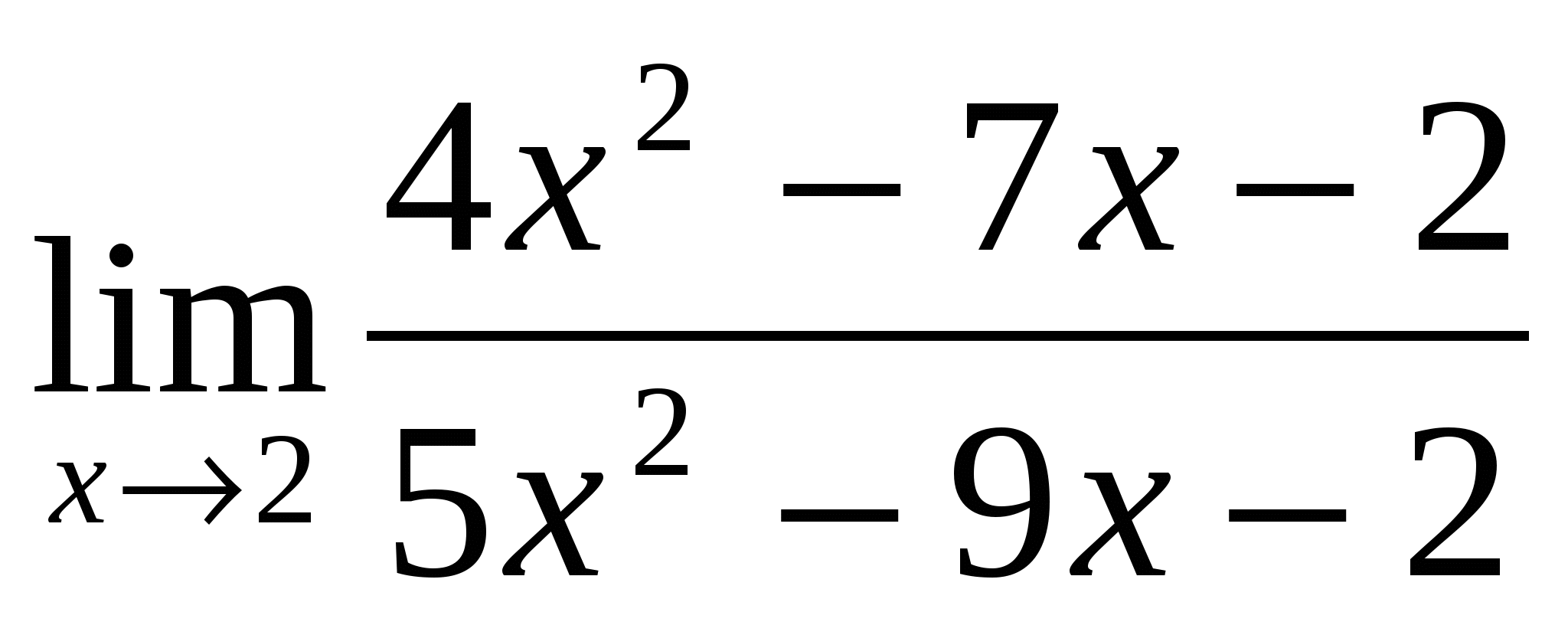
-
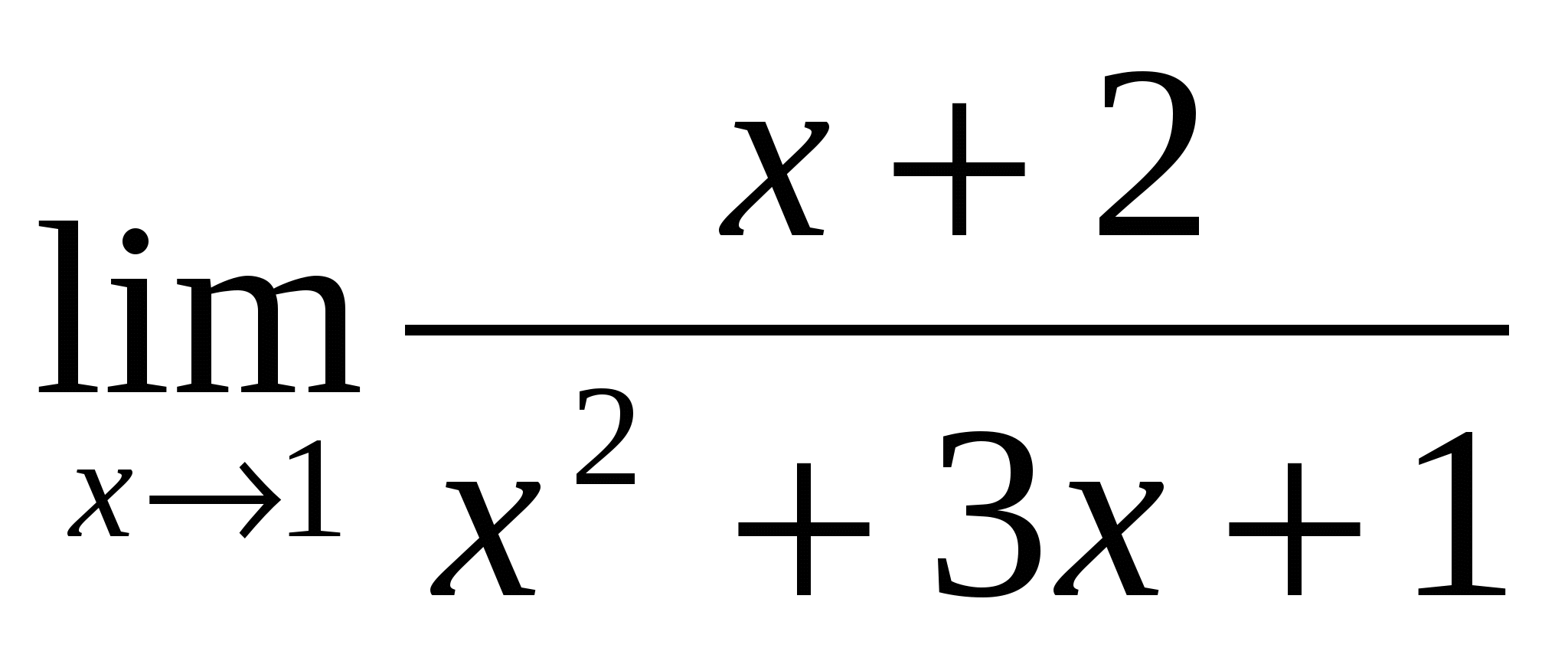
-
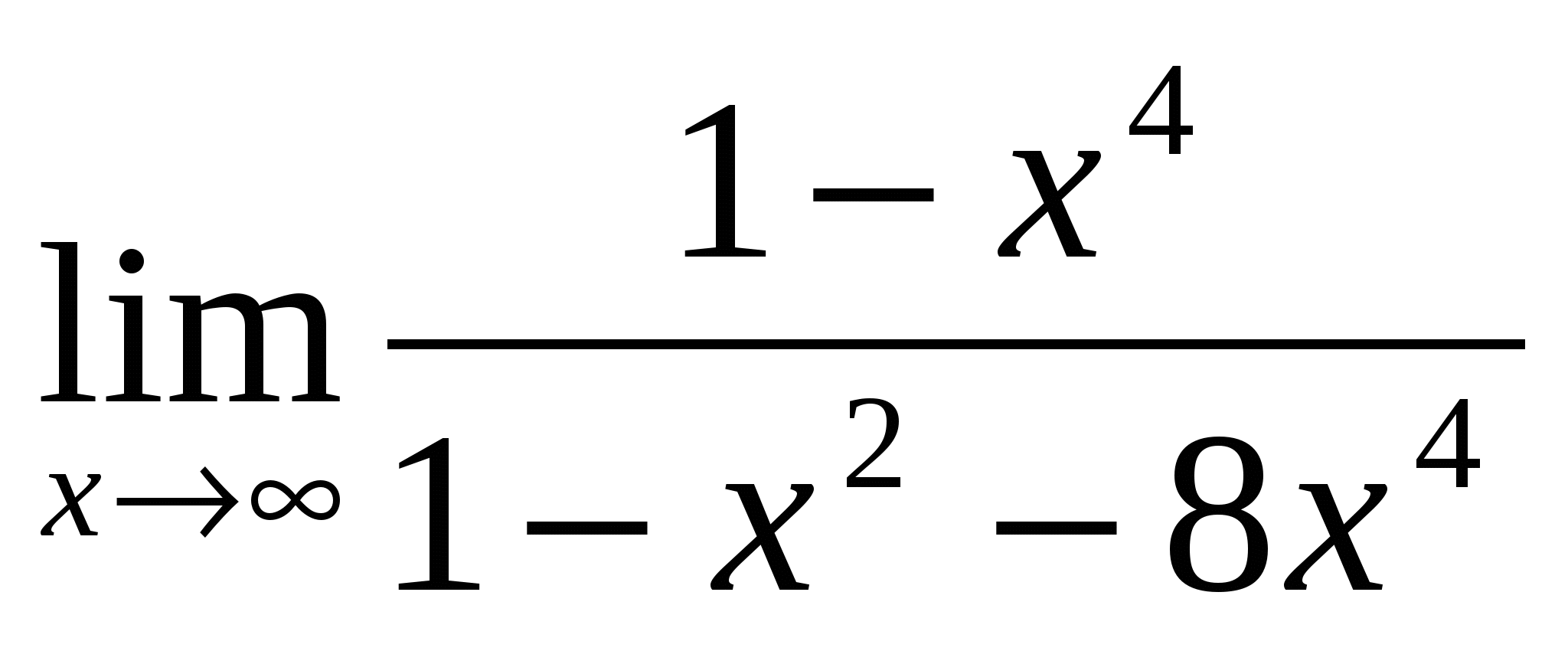
-
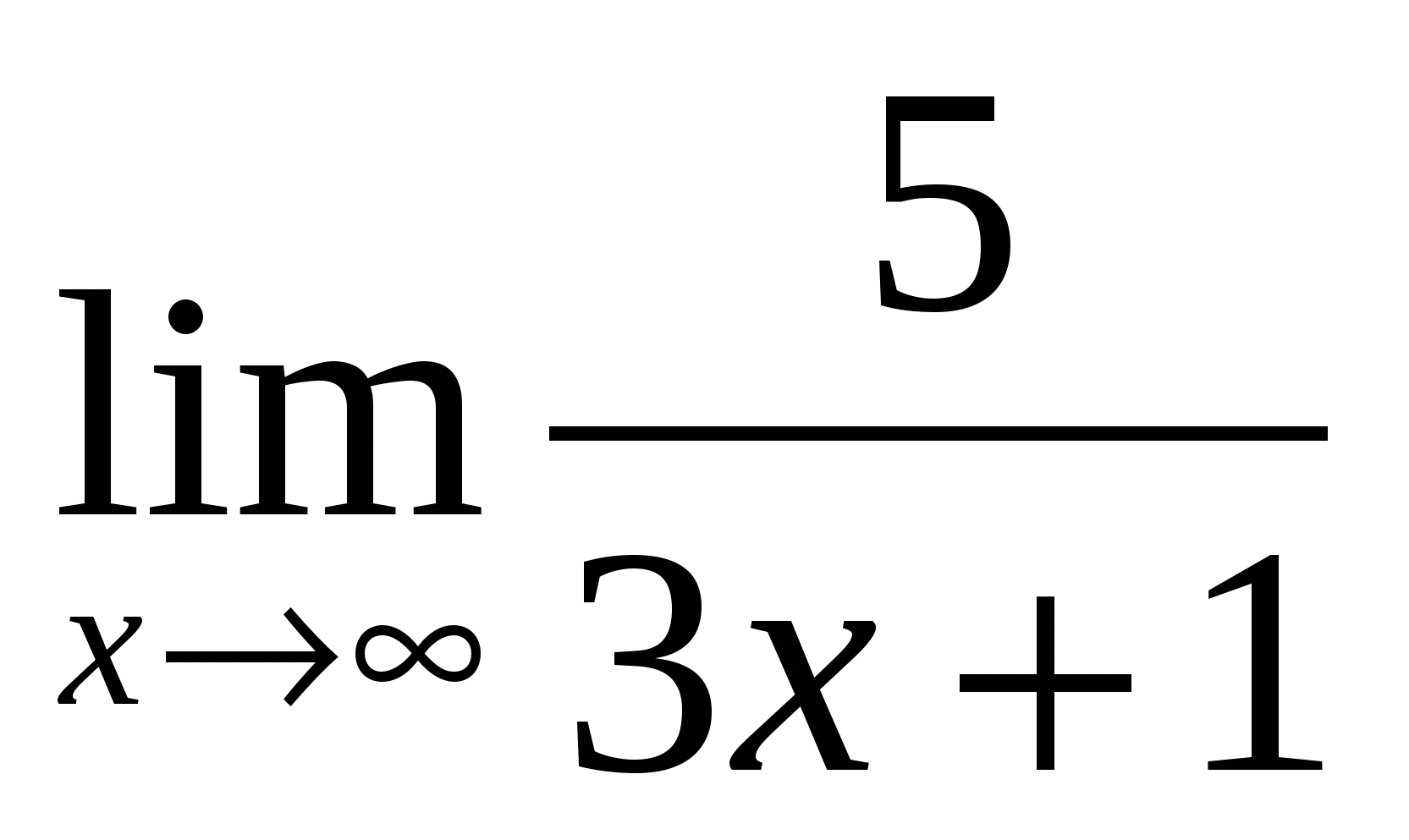
Ответить на вопросы. (Устно)
-
Определение функции.
-
Определение предела функции в точке.
-
Бесконечно малые и бесконечно большие функции. Связь между ними.
-
Правила раскрытия неопределенностей вида
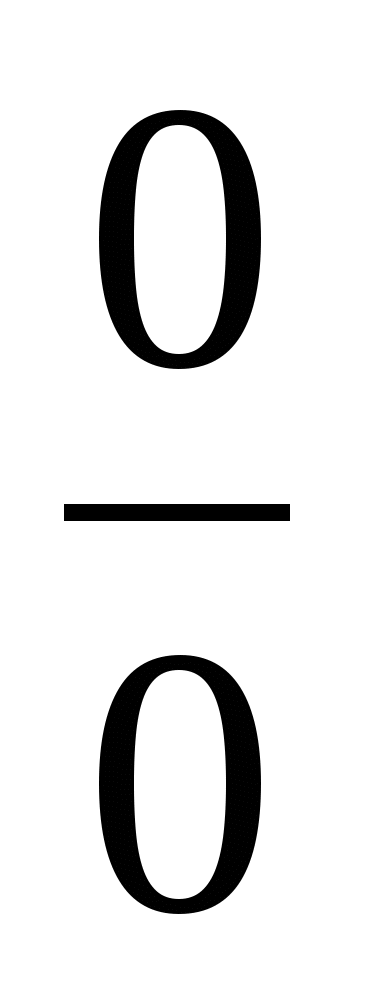 ;
;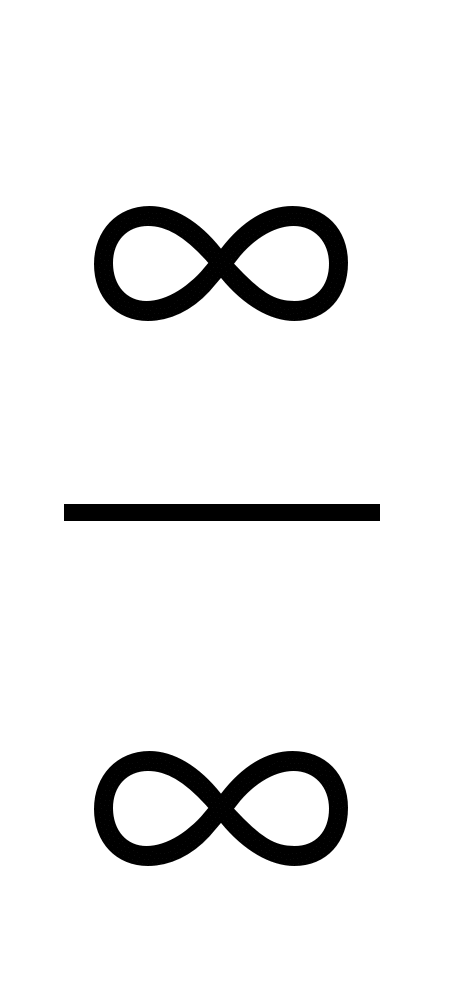 .
.
Решив примеры, группы обмениваются решениями и проверяют их, оценивая.
Затем группам по очереди задаются вопросы преподавателем.
6. Домашнее задание. Вычислить пределы функций. (Инструктаж- 2мин.)
1) ![]() 1)
1) ![]() 3)
3) ![]() 3) 1
3) 1
2) ![]() 2) 5
2) 5
А. Дадаян «Математика» §5.11,§5.12,
Н.Богомолов «Математика» §42
7. Рефлексия. Итоги занятия. Продолжительность работы-6 минут.
Цель: анализ совместной деятельности на уроке.
Задание: каждой группе высказать свои замечания и предложения.
Лидеры групп анализируют работу студентов своих группах, отмечают активно работающих. Преподаватель выставляет оценки.
Преподаватель благодарит студентов за совместное сотрудничество и заканчивает урок.
Преподаватель: Большакова Т.Л.
Здесь представлен конспект к уроку на тему «Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

