Конспект урока «Логарифмическая функция. График и свойства логарифмической функции» по математике для 11 класса
Класс: 11.
Тема урока: Логарифмическая функция. График и свойства логарифмической функции (Слайд 1,2).
Цели урока:
1.Ввести определение логарифмической функции и рассмотреть её свойства.
2. Закрепить знания, умения, навыки по вычислению логарифма и применению свойств логарифмической функции.
3. Воспитывать любовь к математике.
Тип урока: приобретение новых знаний и их закрепление.
Ход урока:
-
Организационный момент. Тренинг «Молекулы и атомы». Ученики хаотично движутся по классу. По команде «Атомы по двое», «Атомы по трое», «Атомы по четверо» и т.д. ученики образуют молекулы. Когда говорим «Атомы», ученики движутся по одному хаотично.
-
Ребята объединились в группы: «Линейная функция», «Показательная функция», «Обратная пропорциональность».
-
Разминка.
А)Найдите логарифмы чисел:
а) ![]()
б) ![]()
Ответы:
а) 4; -1; -3; 0,5; -5;
б) 9; 0,04; 100.
Б) Назовите логарифмы следующих чисел по основанию 3:
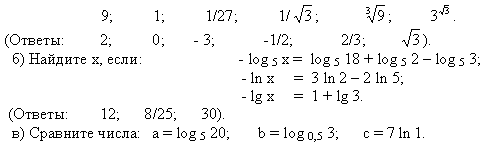
-
Приём критического мышления таблица «Знаем – Хотим узнать – Узнаем» (З – Х – У).
З – знаем Х – хотим узнать У – узнаем
| Х – что мы хотим узнать | У – что мы узнали, и что нам осталось узнать | |
| | | |
| | | |
-
Работа по новому материалу. Стратегия «Чтение с пометкой».
-
Работа с презентацией( Слайд 3-4)
-
Первичное закрепление знаний по вопросам после темы (стр.124)
-
Сулейманов Ренат с докладом «Логарифмы в природе» ( работа с одаренными учащимися).(слайд 5-11)
-
Практическая работа в группах.
Постройте схематически график функции -№ 256 (1,3 пример)
Определите, является ли функция возрастающей или убывающей №257(1,3 пример)
Найдите области определений функций №262 (1,3 пример
-
Блиц опрос
-
Ось Оу является вертикальной асимптотой графика логарифмической функции.
-
Графики показательной и логарифмической функций симметричны относительно прямой у = х.
-
Область определения логарифмической функции – вся
числовая прямая, а область значений этой функции –
промежуток (0, + ∞).
-
Монотонность логарифмической функции зависит от
основания логарифма.
-
Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
-
Логарифмическая функция является ни чётной, ни нечётной.
-
Логарифмическая функция непрерывна.
Взаимопроверка:
| 2 | 3 | 4 | 5 | 6 | 7 | |
| да | да | нет | да | нет | да | да |
-
Рефлексия.
Посмотрите внимательно на те цели, которые мы с вами поставили для сегодняшнего урока:
-
Что на ваш взгляд нам удалось сделать?
-
Что получилось не очень хорошо?
-
Что вам особенно понравилось и запомнилось?
| активно / пассивно | |
| Своей работой на уроке я | доволен / не доволен |
| Урок для меня показался | коротким / длинным |
| За урок я | не устал / устал |
| Моё настроение | стало лучше / стало хуже |
| Материал урока мне был | понятен / не понятен |
| | полезен / бесполезен |
| | интересен / скучен |
-
Выдача домашнего задания. §16 № 260(1-4),263(1,3).
|
|
|
Здесь представлен конспект к уроку на тему «Логарифмическая функция. График и свойства логарифмической функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

