Презентация "Фигуры вращения" по математике – проект, доклад
Презентацию на тему "Фигуры вращения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Фигуры вращения
. Правильные многогранники. Тетраэдр Октаэдр Гексаэдр (куб) Икосаэдр Додекаэдр. Фигуры вращения:. • при вращении тетраэдра в зависимости от оси вращения, ...Фигуры вращения
ФИГУРЫ ВРАЩЕНИЯ. Говорят,что фигура Ф в пространстве получена вращением фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами ...Фигуры
ЦВЕТОК. ЁЛКА. ЗАЯЦ. ГРУЗОВИК. КОШКА. ТЕЛЕФОН АЛЁ. РЫБА. ГРИБ. МЫШКА. ...Тела и поверхности вращения
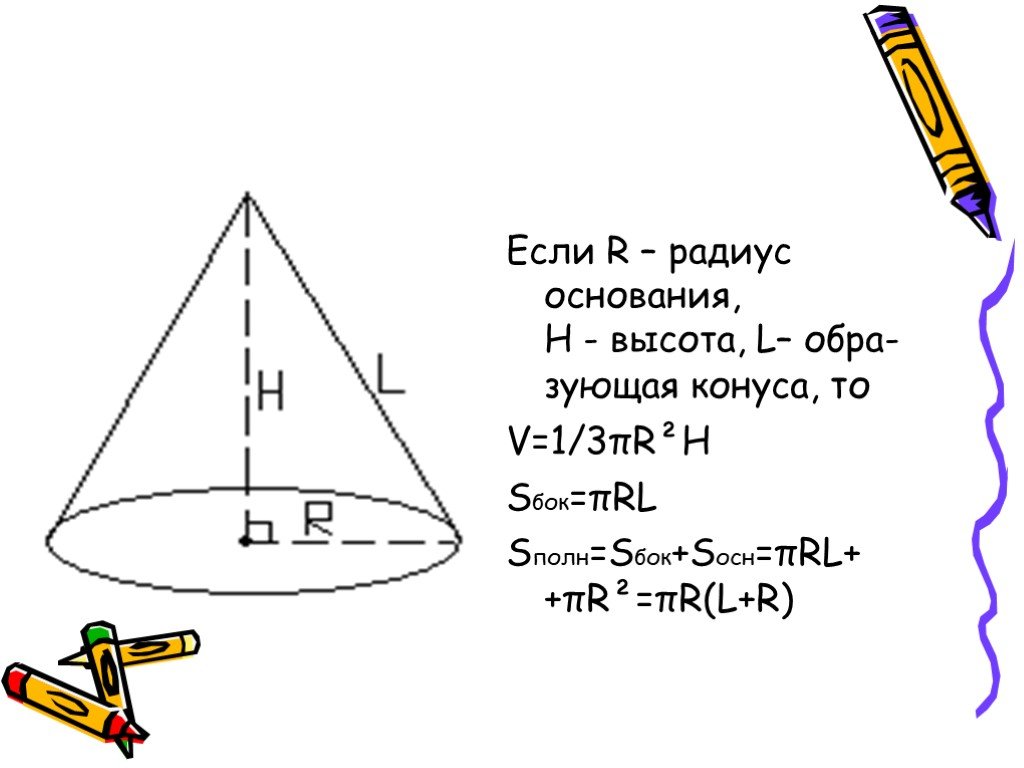
Цилиндр Ось цилиндра. Основание цилиндра. Образующие цилиндра. Радиус цилиндра. h 2Пr S = 2Пrh бок V = S h осн. О А Р Конус Ось конуса Основание конуса ...Тела вращения вокруг нас
Задачи: Использование комбинации тел вращения в архитектуре Тела вращения созданые самой природой Использование комбинации тел вращения в технике. ...Тела вращения
Цилиндр Конус Шар и сфера Содержание. Левый клик по названию раздела. Тело вращение – это пространственная фигура полученная вращением плоской ограниченной ...Тела вращения
Какое геометрическое тело получится при вращении данного треугольника около указанной оси? Какое геометрическое тело получится при вращении ромба ...Геометрические тела вращения
МОУ Степановская СОШ. Костромская область Галичский район Д. Степаново Ул. Центральная д.10 Учитель: Елесина Галина Витальевна. Цели и задачи. Повторить ...Фигуры на плоскости
Содержание:. Параллелограмм. Прямоугольник. Ромб. Квадрат. Трапеция. Параллелограмм. Рисунок. Площадь параллелограмма равна произведению его стороны ...Тела вращения
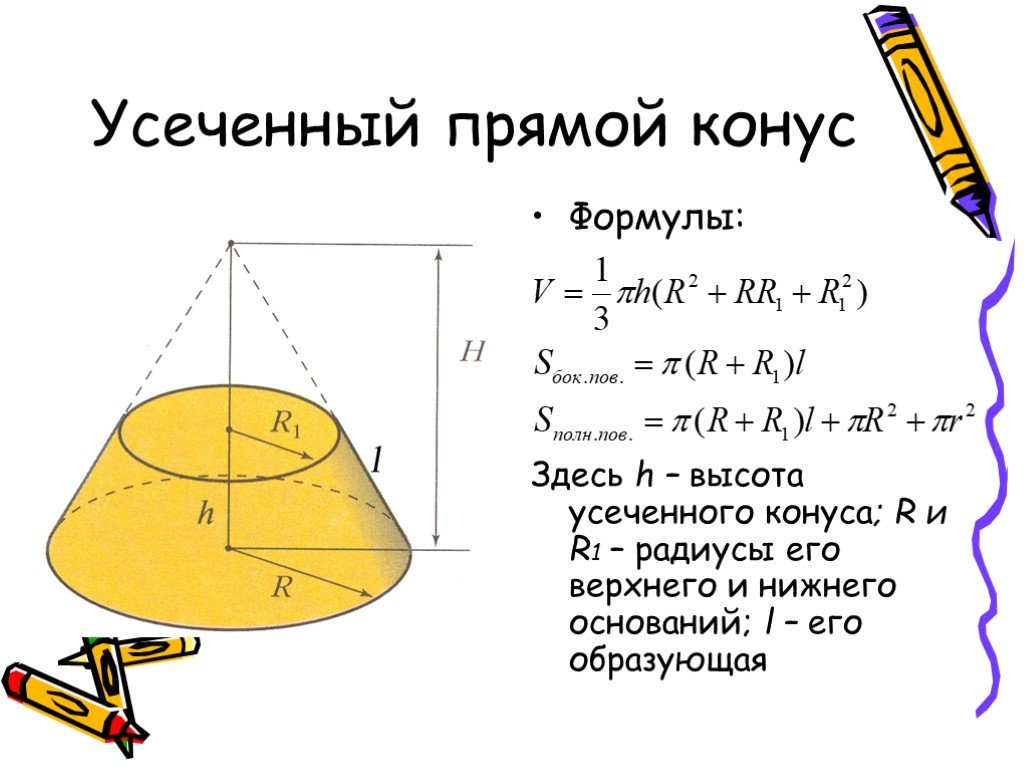
Цель урока:. 1. Познакомить учащихся с формулами для вычисления объёмов цилиндра, конуса, усечённого конуса, научить применять их при решении задач;. ...Тела вращения
Содержание. Происхождение названий Определения Примеры тел вращений Объёмы и поверхности Задачи. «Цилиндр» - греческое слово «kylindros», что означает ...Тела вращения
Концы отрезка АВ, равного а, лежат на окружностях основания цилиндра. Радиус цилиндра равен r, высота h, расстояние между прямой АВ и осью ОО1 цилиндра ...Многогранники. Тела вращения
Тела вращения. Проверка теста. Задача 1. Молоко переливают в пол-литровую банку с помощью шестигранного стакана. Сколько стаканов молока войдет в ...Комбинации шара с многогранниками и фигурами вращения
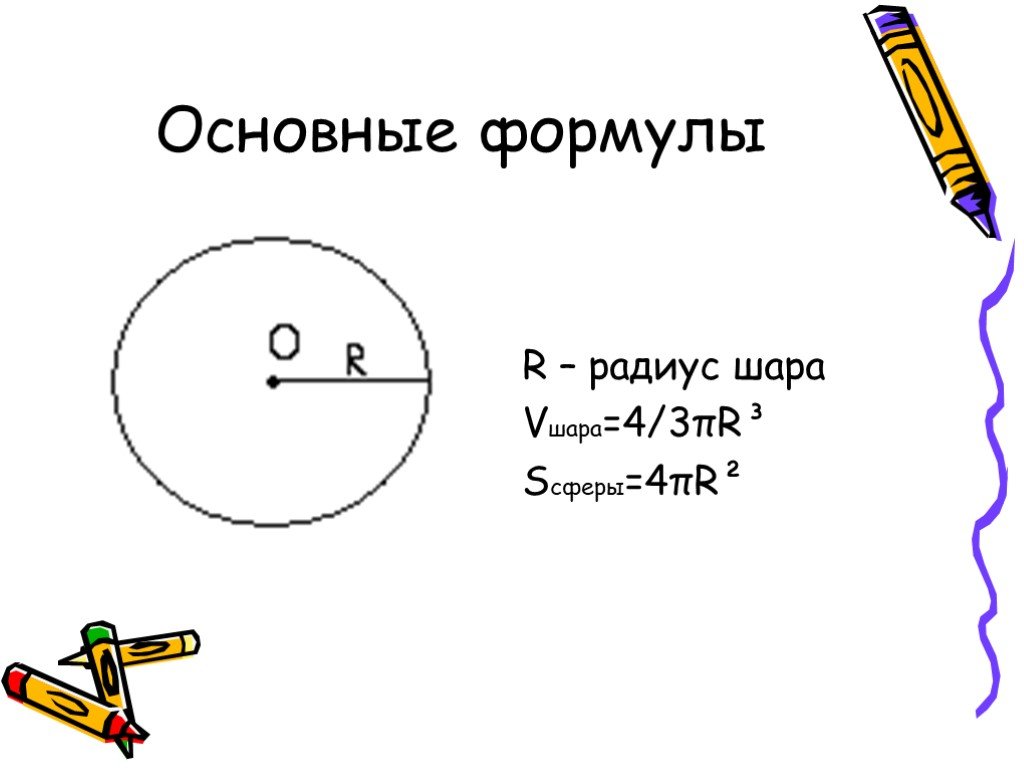
Шар (сфера) называются описанными около многогранника, если все вершины многогранника принадлежат поверхности шара (сфере). R. R – радиус шара (сферы), ...История изучения тел вращения
Первоначальные сведения о свойствах геометрических тел люди нашли, наблюдая окружающий мир и в результате практической деятельности. Со временем ученые ...Тела вращения
Объём цилиндра. Объём цилиндра равен произведению площади основания на высоту. Объём конуса. Объём конуса равен одной трети произведения площади основания ...Тела вращения
Цилиндр. Круговой цилиндр – тело, которое состоит из двух равных кругов, лежащих в параллельных плоскостях, и всех отрезков, соединяющих соответствующие ...Фигуры с равными периметрами
«Пускай мы Пифагорами не станем! А вдруг?». Бывает ли геометрия «экономной»? Проблемно-тематический вопрос. Основополагающий вопрос. Что было бы, ...Вычислить объём тела вращения
ОПРЕДЕЛЕНИЕ ЦИЛИНДРА. Цили́ндр (др.-греч. κύλινδρος — валик, каток) Цилиндр - тело, ограниченное цилиндрической поверхностью и двумя кругами с границами ...Конспекты
Фигуры и тела вращения
Урок геометрии в 11 классе по теме «Фигуры и тела вращения». «Предмет математики настолько серьёзен, что надо. не упускать возможности. ...Тела вращения - КОНУС
. ПЛАН. Открытого урока по математике. Тема: Тела вращения -. КОНУС. Подготовила преподаватель математики. ...Фигуры
Открытое занятие по математике. . В предшкольной группе. Тема:. Фигуры. Программный материал и цели:. Познакомить детей с геометрическими ...Тела вращения
МБОУ «Корниловская СОШ». Урок геометрии в 11 классе по теме. . «Тела вращения». Учитель математики. Фефилатьева Валентина. ...Тела вращения
Методическая разработка урока по математике. Тема"Тела вращения". Предмет математики настолько серьёзен, что надо не упускать возможности сделать ...Тела вращения
КОНСПЕКТ УРОКА. Тема урока:. Тела вращения. Класс:. 11. Цели урока:. 1. Организовать деятельность учащихся по обобщению и систематизации знаний ...Решение задач на тела вращения
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ГИМНАЗИЯ №40» г. БАРНАУЛА. МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА. «Современные ...Решение задач на вычисление объемов тел вращения
Конспект урока. Предмет, класс. :. «Геометрия», 11«б» класс. (класс с углубленным изучением математики). Тема. :. «Решение задач на вычисление ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 ноября 2018
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию









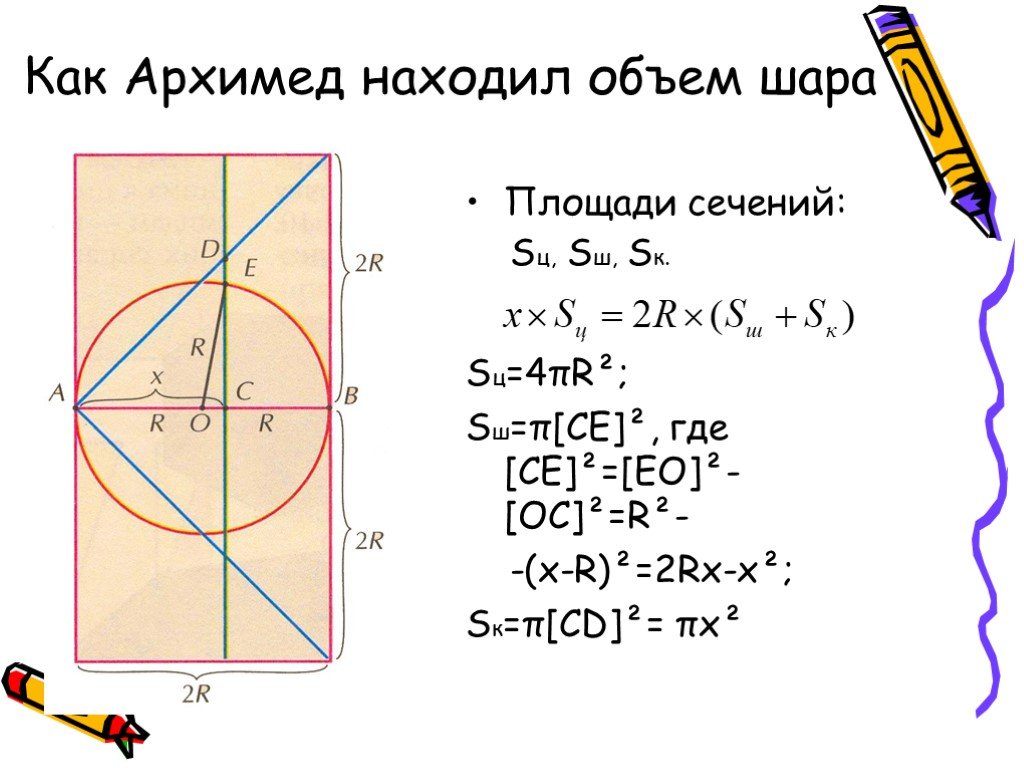
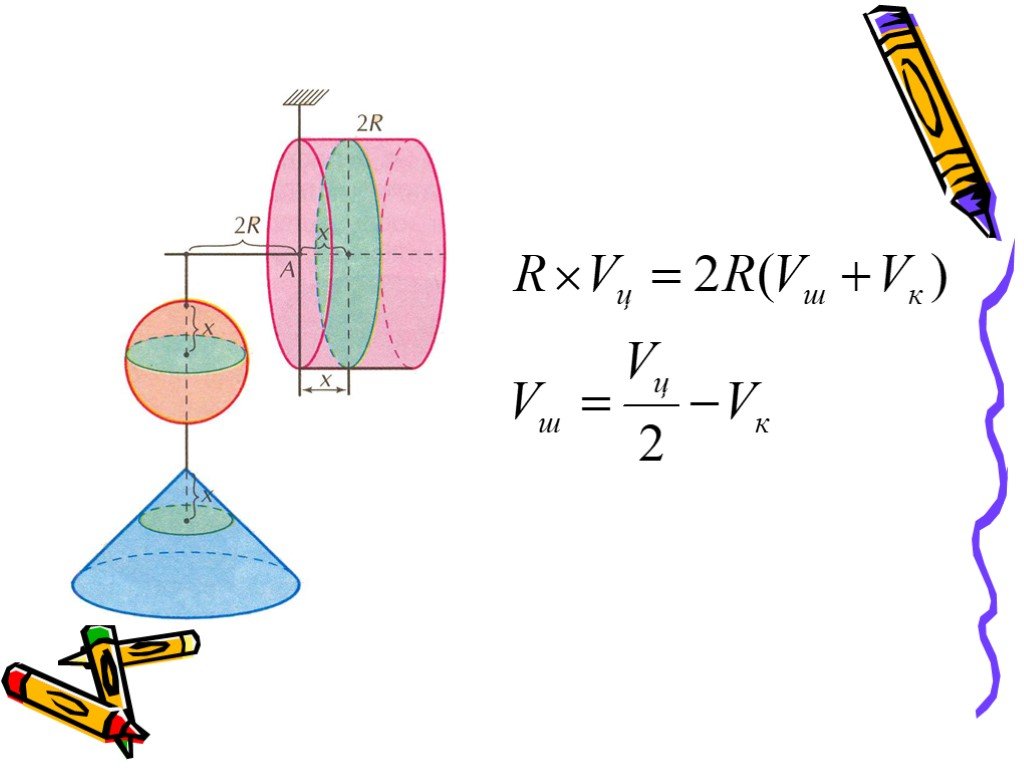














![Как Архимед находил объем шара. Площади сечений: Sц, Sш, Sк. Sц=4πR²; Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²; Sк=π[CD]²= πx² Как Архимед находил объем шара. Площади сечений: Sц, Sш, Sк. Sц=4πR²; Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²; Sк=π[CD]²= πx²](https://prezentacii.org/upload/cloud/18/11/95680/images/thumbs/screen14.jpg)