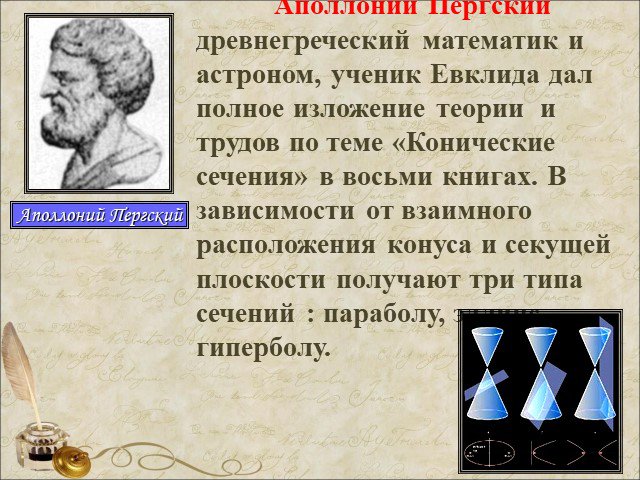
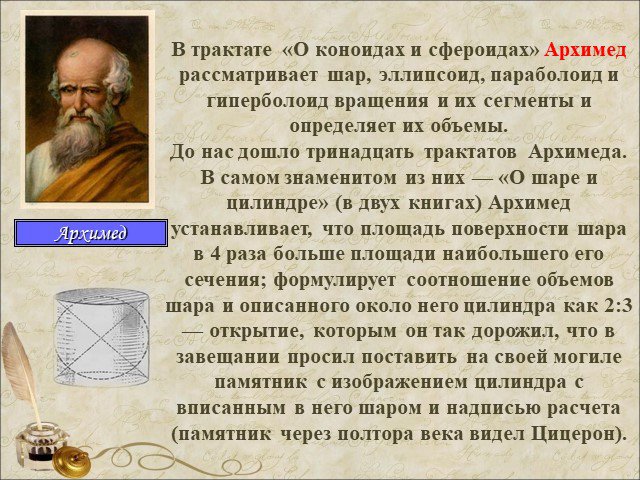
Презентация "История изучения тел вращения" по математике – проект, доклад

История изучения тел вращения

Выполнила: учитель математики высшей категории МБОУ СОШ №1 г.Воткинска Колесникова Татьяна Павловна

Первоначальные сведения о свойствах геометрических тел люди нашли, наблюдая окружающий мир и в результате практической деятельности. Со временем ученые заметили, что некоторые свойства геометрических тел можно выводить из других свойств путем рассуждения. Так возникли теоремы и доказательства.

Начальные сведения о свойствах тел вращения относятся ко времени зарождения геометрии как будущей математической науки. Еще за тысячи лет до наших времен земледельцы пытались хотя бы приблизительно узнать о собранном урожае, вычисляя размеры куч зерна и тех емкостей, где зерно сохраняли.

В связи с развитием мореплавании были нужны астрономические наблюдения, что заставляло человека изучать свойства шара и его частей. Длительное время зависимости между геометрическими величинами, с помощью которых производились различные вычисления, употреблялись как некоторые практические правила, без должного обоснования.

Уже в 7 в. до н.э. в Греции начали накапливаться знания в области, стереометрии, вырабатывались приемы математических рассуждений.

В области геометрии египтяне знали точные формулы для площади прямоугольника, треугольника и трапеции. Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. Площадь круга вычислялась, исходя из предположения =3,1605 (погрешность менее 1 %). Египтяне знали точные формулы для объёма параллелепипеда и различных цилиндрических тел, а также пирамиды и усечённой пирамиды. Пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле:

Цилиндр, шар и сфера – слова греческого происхождения, конус – латинское слово, заимствованное из греческого. В переводе на русский язык цилиндр – валик, каток; конус – затычка, втулка, сосновая шишка. Шар и сфера – происходят от одного и того же греческого слова «сфайра» - мяч. Евклид в 11-й книге «Начал» дал определение цилиндра, шара и конуса как тел вращения. Задача вычисления объёмов, идущая из практических потребностей , была одним из стимулов развития геометрии. Математика Древнего Востока (Вавилония, Египет) располагала рядом правил для вычисления объёмов (большей частью эмпирических). Греческая математика последних столетий до нашей эры освободила теорию вычисления объёмов от приближённых эмпирических правил. В «Началах» Евклида и в сочинениях Архимеда имеются только точные правила вычисления объёмов цилиндра, конуса, шара и их частей.

Начали формироваться общие представления о пространственных фигурах и способах доказательства их свойств. Важная роль в изложении сведений по стереометрии в определенной логической последовательности принадлежит греческому математику Евклиду ( 3 в. до н.э. ), автору известного научного сочинения " Начала ", состоящему из 13 книг.

Имя Евклида упоминается в первом из двух писем Архимеда к Досифею «О шаре и цилиндре». С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. В XI книге «Начал» дается определение конуса.  Евклид рассматривает  только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию, лишь Аполлоний различает прямые и косые конусы, у которых ось образует с основанием угол, отличный от прямого. У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”.

Евклид

Аполлоний Пергский древнегреческий математик и астроном, ученик Евклида дал полное изложение теории и трудов по теме «Конические сечения» в восьми книгах. В зависимости от взаимного расположения конуса и секущей плоскости получают три типа сечений : параболу, эллипс, гиперболу.

Аполлоний Пергский

Другой знаменитый древнегреческий математик Архимед ( 3 в. до н.э. ) Боковая поверхность цилиндра, конуса, объёмы шара и сферического сегмента, а также объёмы различных тел вращения найдены Архимедом. Вывод формулы объёма шара и площади сферы – одно из величайших открытий Архимеда. В его произведении «О шаре и цилиндре» есть следующие теоремы: Объём шара равен учетверённому объёму конуса, основанием которого служит большой круг, а высотой радиус шара, то есть V= πR3

Объём цилиндра в полтора раза больше объёма вписанного в него шара.

В трактате «О коноидах и сфероидах» Архимед рассматривает шар, эллипсоид, параболоид и гиперболоид вращения и их сегменты и определяет их объемы. До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» (в двух книгах) Архимед устанавливает, что площадь поверхности шара в 4 раза больше площади наибольшего его сечения; формулирует соотношение объемов шара и описанного около него цилиндра как 2:3 — открытие, которым он так дорожил, что в завещании просил поставить на своей могиле памятник с изображением цилиндра с вписанным в него шаром и надписью расчета (памятник через полтора века видел Цицерон).

Архимед

Формулу вычисления объёма конуса даёт Герон Александрийский.

великий физик, математик, механик и инженер древней Греции. Жил предположительно в I-II века до нашей эры в Александрии Египетской. Много работ Герона Александрийского было посвящено Математике. Больше всего в его работах формул по геометрии, задач по вычислению геометрических фигур. Так же здесь описывается и знаменитая формула Герона, с помощью которой можно вычислить площадь треугольника по трем сторонам. Надо отметить, что открыл эту формулу все-таки Архимед, а не Герон. Большинство формул приведенных Героном Александрийским в своих книгах приводятся без всяких доказательств, только с примерами.

«Метрика» (Μετρική) Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений: Формулы для площадей правильных многоугольников. Объёмы правильных многогранников, пирамиды, конуса, усечённого конуса, тора, шарового сегмента. Формула Герона для расчёта площади треугольника по длинам его сторон (открытая Архимедом).

Содержание математических трудов Герона догматично, правила чаще всего не выводятся, а поясняются на примерах. Это сближает труды Герона с работами математиков Древнего Египта и Вавилона

Труды Евклида и Архимеда после их перевода на арабский язык, а с арабского на латинский проникают в Европу и создают основу для составления учебников для средних школ.

Сейчас мы знаем, что аналитически объём может быть выражен с помощью интегралов. Исторически происходило так, что задолго до создания интегрального исчисления операция интегрирования фактически применялась к вычислению объёмов некоторых тел вращения, чем и была подготовлена почва для развития интегрального исчисления в 17-18 веках. .

Жозеф Луи Лагранж (Joseph Louis Lagrange) Даты жизни: 25 января 1736 – 10 апреля 1813 Лагранж родился в Турине. Из-за материальных затруднений семьи он был вынужден рано начать самостоятельную жизнь. Сначала Лагранж заинтересовался филологией. Его отец хотел, чтобы сын стал адвокатом, и поэтому определил его в Туринский университет. Но в руки Лагранжа случайно попал трактат по математической оптике, и он почувствовал своё настоящее призвание. В 1755 году Лагранж послал Эйлеру свою работу об изопериметрических свойствах, ставших впоследствии основой вариационного исчисления. В этой работе он решил ряд задач, которые сам Эйлер не смог одолеть.

В середине 18 века Эйлер и Лагранж свободно владели двойным и тройным интегралами. В 1756 году Лагранж выразил с их помощью объёмы цилиндрических тел и площади криволинейных поверхностей

Эйлер Леонард 15 апреля 1707 года - 18 сентября 1783 года Родился в семье небогатого пастора Пауля Эйлера. Образование получил сначала у отца (который в молодости занимался математикой под руководством Я. Бернулли), а в 1720-1724 годы в Базельском университете, где слушал лекции по математике И. Бернулли. В конце 1726 года Эйлер был приглашен в Петербургскую АН и в мае 1727 года приехал в Петербург. В только что организованной Петром 1 академии Эйлер нашёл благоприятные условия для научной деятельности, что позволило ему сразу же приступить к занятиям математикой и механикой. За 14 лет первого петербургского периода жизни Эйлер подготовил к печати около 80 трудов и опубликовал свыше 50. В Петербурге он очень быстро изучил русский язык.

За время существования Академии наук в России, видимо, одним из самых знаменитых ее членов был математик Леонард Эйлер.

Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. С точки зрения математики, XVIII век — это век Эйлера. Если до него достижения в области математики были разрознены и не всегда согласованы, то Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».

Эйлер значительно продвинул аналитическую геометрию, особенно учение о поверхностях 2-го порядка. В дифференциальной геометрии он детально исследовал свойства геодезических линий, впервые применил натуральные уравнения кривых, а главное, заложил основы теории поверхностей. Он ввёл понятие главных направлений в точке поверхности, доказал их ортогональность, вывел формулу для кривизны любого нормального сечения, начал изучение развёртывающихся поверхностей и т.д.; в одной посмертно опубликованной работе (1862) он частично предварил исследования К. Ф. Гаусса по внутренней геометрии поверхностей. Эйлер занимался и отдельными вопросами топологии и доказал, например, важную теорему о выпуклых многогранниках. Эйлера-математика нередко характеризуют как гениального "вычислителя". Действительно, он был непревзойдённым мастером формальных выкладок и преобразований, в его трудах многие математические формулы и символика получили современный вид. Однако Эйлер был не только исключительной силы "вычислителем". Он внёс в науку ряд глубоких идей, которые ныне строго обоснованы и служат образцом глубины проникновения в предмет исследования.

Спасибо за внимание!