Презентация "Вычисление объемов пространственных тел" по математике – проект, доклад
Презентацию на тему "Вычисление объемов пространственных тел" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
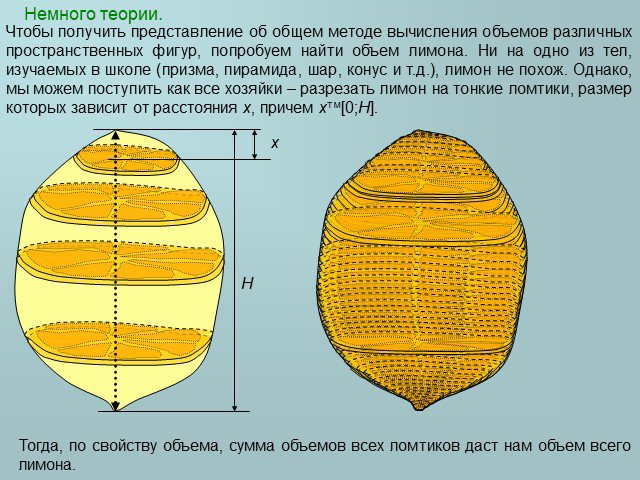
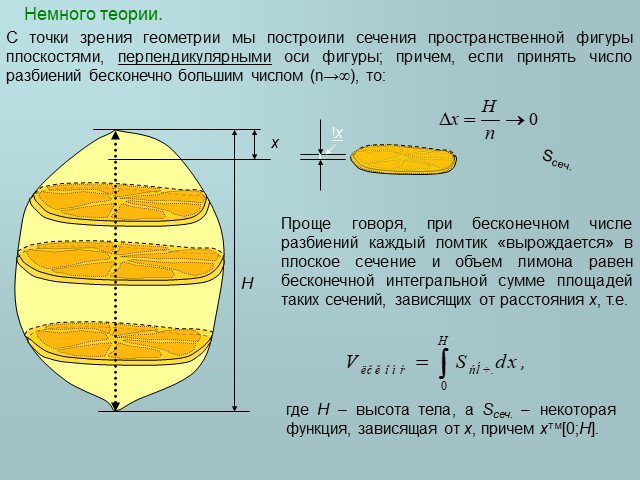
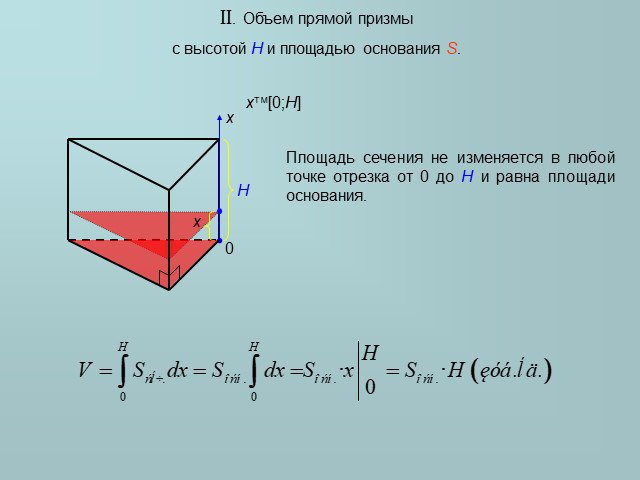
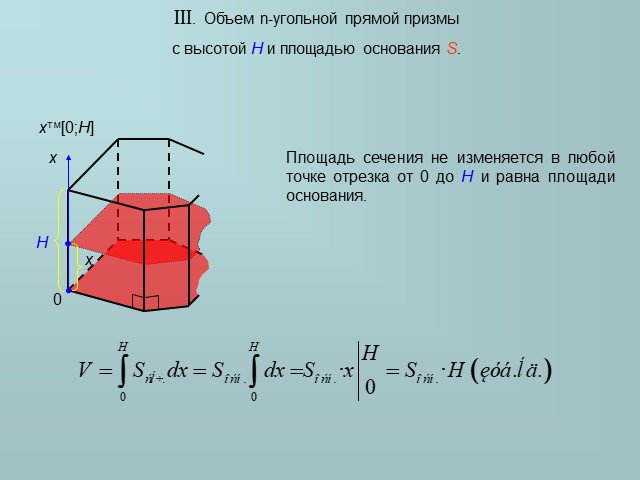
Слайды презентации
Список похожих презентаций
Вычисление объема тела человека
Архимед (287 - 212 до н.э.). Древнегреческий ученый математик и изобретатель, родился в Сиракузах. Закон Архимеда формулируется так:. Архимедова сила, ...Вычисление площадей фигур в ходе экспериментальной деятельности
Цели:. Проверить умение проводить экспериментальную работу и на основании полученных результатов выдвигать гипотезы, делать выводы; Проверить степень ...Вычисление производной
Аннотация Это урок-практикум по теме «Вычисление производной». Урок проводится с применением интерактивной доски. Продолжительность 15 минут. На данном ...Вычисление приделов
План. 1. Определение предела 2. Теоремы 3. Примеры вычисления приделов 4. Литература. 1. Определение предела. Число b – предел функции f(x) при x ...Вычисление площади с помощью палетки
Найди «лишние» фигуры и обоснуй ответ. Как найти площадь этих фигур? ? АЛГОРИТМ. Наложить палетку на фигуру Сосчитать число целых клеток Сосчитать ...Вычисление площади криволинейной трапеции
Тема урока:. криволинейной трапеции». «Вычисление площади. Цели урока. 1. Найти способы решения задач различного уровня сложности 2. С помощью знаний ...Вычисление десятичных дробей
Урок математики в 5 классе. Путешествие в сказку Тема «Сложение и вычитание десятичных дробей». Содержание. 1 слайд Титульный 2 слайд Заголовок 3 ...История изучения тел вращения
Первоначальные сведения о свойствах геометрических тел люди нашли, наблюдая окружающий мир и в результате практической деятельности. Со временем ученые ...Вычисление тройных интегралов
. 1 2. Проектируем поверхность, ограниченную объемом V, на плоскость ХОУ, получаем область D. Определяем координаты точек z1 (x,y) и z2 (x,y) входа ...Вычисление площадей плоских фигур с помощью определенного интеграла
ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ВЫ УЗНАЕТЕ ОДНО ИЗ ВЫСКАЗЫВАНИЙ ФРАНЦУЗСКОГО МАТЕМАТИКА С.Д.ПУАССОНА. Жизнь украшается двумя вещами: занятием математикой ...Вычисление площадей плоских фигур с помощью определенного интеграла
Плоские фигуры a b y = f(x) y = g(x). Р M K C D. . Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x, y = 5 – x, x = 1, x = 2. 0 1 2. ...Вычисление площадей плоских фигур
Содержание. 1.Фигуры 2.Параллелограмм 3.Прямоугольник 4.Ромб 5.Квадрат 6.Треугольник 7.Трапеция 8. Круг 9.Примеры вычисления площадей фигур. Клинкова ...Вычисление объёма цилиндра
Устные упражнения по теме. Решение стереометрических задач. Выполнение практической работы. Самостоятельная работа. План урока. Чтобы избегать ошибок, ...Вычисление объёма фигур
Вычисление объёма фигур. Грань. Вершина. Ребро. Длина Высота Ширина. Формула объёма V = a. V = a∙b. V = a∙b∙c. . Единицы измерения объёма. 1 кубический ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Вычисление производных
План урока. Актуализация полученных знаний. Обобщение ранее изученного материала: а) устные упражнения б) письменные упражнения Физкультминутка Выполнение ...Вычисление площадей с помощью интегралов
Знаем:. 1.Как вычислить интеграл. 2. Что такое криволинейная трапеция. 3. Как связаны площадь криволинейной трапеции с интегралом. Криволинейной трапецией ...Изображение пространственных фигур
Для изображения пространственных фигур используют параллельную проекцию. Плоскость, на которую проектируется фигура, называется плоскостью изображений, ...Вычисление площади криволинейной трапеции
Найти первообразную функции:. 1 задание 2 задание*. устно. 1. Какая фигура называется криволинейной трапецией? 2 3. Как найти площадь криволинейной ...Комбинации геометрических тел
Цилиндр и призма. Цилиндр, описанный около призмы. Цилиндр, вписанный в призму. Конус и пирамида. Конус, описанный около пирамиды. Конус, вписанный ...Конспекты
Вычисление значений выражений, содержащих степени
Урок закрепления. Тема урока. «Вычисление значений выражений, содержащих степени». Цели урока:. образовательная. –. обобщение и развитие знаний ...Объем и площадь поверхности конических тел
Урок 4. Тема урока: «Объем и площадь поверхности конических тел». Тип учебного занятия:. изучение и первичное закрепление новых знаний и способов ...Площадь. Вычисление площади фигур различной конфигурации
Геометрия. . 4 кл. Учитель: Крамаренко Н.Н. Тема:. Площадь. Вычисление площади фигур различной конфигурации. Цели:. 1) Учить находить площади ...Вычисление производных элементарных функций
Пузик Ирина Николаевна,. . учитель математики МКОУ СОШ №17 р.п Юрты Тайшетского района Иркутской области. Тема урока: Вычисление производных ...Задача. Вычисление и запись ответа
Урок математики в 1 классе. Программа: «Перспективная начальная школа». Учебник: математика 1 класс, автор: А. Л. Чекин. Тетрадь № 2 для самостоятельной ...Вычисление производных
Краевое государственное бюджетное профессиональное. . образовательное учреждение. . «Спасский политехнический колледж». Методическая разработка ...Вычисление производных функций
Технологическая карта урока. Ф.И.О. учителя: Терентьева Елена Аркадьевна. Класс: 11 общеобразовательной школы при ФКУ ИК. Дата: 17.12.2014. Предмет. ...Вычисление площадей
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. САМАРСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА. КУРКИНСКОГО РАЙОНА ТУЛЬСКОЙ ОБЛАСТИ. КОНСПЕКТ ...Вычисление площадей плоских фигур с помощью определенного интеграла
7. . . Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа с. Успеновка. ...Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда
Конспект урока по математике 4 класс. Тема: «Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда». Подготовила: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Воробьев Леонид Альбертович
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию












![I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x[0;H] 0. Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания. I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x[0;H] 0. Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания.](https://prezentacii.org/upload/cloud/14/09/6107/images/thumbs/screen5.jpg)











































