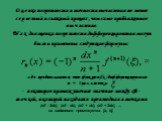Презентация "Вычисление производной функции" по математике – проект, доклад
Презентацию на тему "Вычисление производной функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
Определение производной от функции
Определение производной функции (Содержание). Геометрический смысл отношения Геометрический смысл отношения при Геометрический смысл производной функции ...Понятие о производной функции
Цели урока:. ОБУЧАЮЩАЯ : 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический смысл производной; 2) ...Применение производной функции
с и л а. в у м е. I вариант II вариант Буква С Буква В. Буква И Буква У. Буква Л Буква М. Буква А Буква Е 7. Сложилась фраза. ...Применения производной к исследованию функции
(можно использовать как ссылки) Из истории Понятия производной Определение производной Правила дифференцирования и таблица производных Примеры применения ...Исследование функции с помощью производной
Исследование функции с помощью производной. УСТНЫЙ ОПРОС. Достаточный признак возрастания функции. Достаточный признак убывания функции. Какие точки ...Применение производной к исследованию функции
Применение производной к исследованию функции. Критические точки функции. х у у = g (х) у = f (х). Повторение: описание свойств функции по её графику ...Исследование функции производной
Цели урока: выяснение степени усвоения . правил вычисления производных; дать понятие «промежутка монотонности функции» уметь применять производную ...Исследование функции с помощью производной
Правила дифференцирования. Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения ...Понятие производной функции
Автор Сизова Н. В., г. Саров. Производная. Историческая справка. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Исследование графика функции с помощью производной.
Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4] функции. -7 4 Y=f'(x) проверка 0 1 X Y Y=f‘(x). ...Физический и геометрический смыслы производной. Уравнение касательной к графику функции
Цели урока:. • Проверить умения применять формулы и правила вычисления производных. Знать физический и геометрический смысл производной, уравнений ...Задачи на нахождение производной степенной функции
Повторение опорного материала: а) теоретическая часть. Что называется производной функции у(х) ? Сформулируйте правила дифференцирования Запишите ...«Применение производной для исследования функции»
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько ...Производная функции. Геометрический смысл производной
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная. Производная. — это скорость ...Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...Вычисление производной
Аннотация Это урок-практикум по теме «Вычисление производной». Урок проводится с применением интерактивной доски. Продолжительность 15 минут. На данном ...Применение производной для исследования функции на монотонность и экстремумы
Х У 0 касательная α. k – угловой коэффициент прямой (касательной). Геометрический смысл производной: если к графику функции y = f(x) в точке с абсциссой ...Практическое применение производной
ОБУЧАЮЩАЯ :. повторить, обобщить, систематизировать знания по данной теме ; показать учащимся необходимость знания материала изученной темы при решении ...Вычисление объема тела человека
Архимед (287 - 212 до н.э.). Древнегреческий ученый математик и изобретатель, родился в Сиракузах. Закон Архимеда формулируется так:. Архимедова сила, ...Конспекты
Исследование функции с помощью производной
Опорный конспект. . «Исследование функции с помощью производной. ». ГАОУ СПО ВПТК. Зотова И.В., преподаватель математики. Найти область ...Понятие о производной функции. Ее геометрический и физический смысл
Дата. . Класс. . Предмет. . . 14.11.2013. . . 11. . Алгебра и начала анализа. . . . Тема урока:. Понятие о производной ...Применение производной к исследованию функций. Наибольшее и наименьшее значение функции
ГОУ «Школа здоровья и индивидуального развития». Красногвардейского района. Санкт-Петербурга. Урок алгебры и начал анализа. ...Применение производной к исследованию функции
Урок 49. Тема урока:. «Применение производной к исследованию функции». Предмет:. Алгебра и начала анализа. Тип занятия:. закрепления изученного ...Применение производной к исследованию функции
Обобщающий урок в 11 классе по теме. «Применение производной к исследованию функции». Цель урока:. Систематизирование и обобщение знаний ...Применение производной к исследованию свойств функции и к решению прикладных задач
Конспект урока алгебры для учащихся 10 класса. Тема урока:. Применение производной к исследованию свойств функции и к решению прикладных задач. ...Исследование функции с помощью производной
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №151 Красногвардейского района Санкт-Петербурга. 195426, ...Применение производной к исследованию функции
МОУ Греково-Степановская СОШ. . Чертковского района Ростовской области. Учитель математики и информатики. Киселева Лариса Анатольевна. Урок алгебры ...Вычисление производной
муниципальное бюджетное общеобразовательное учреждение «Тат.Ходяшевская средняя общеобразовательная школа». Пестречинского муни. ц. ипального района ...Исследование функции с помощью производной
Выездное заседание республиканского клуба «Пеликан». 20 марта 2012 г. План-конспект урока. Тема «Исследование функции с помощью производной». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2019
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию