Презентация "Практическое применение производной" по математике – проект, доклад
Презентацию на тему "Практическое применение производной" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Применение производной
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце 17 столетия. Тем более поразительно, что за долго до этого ...«Применение производной для исследования функции»
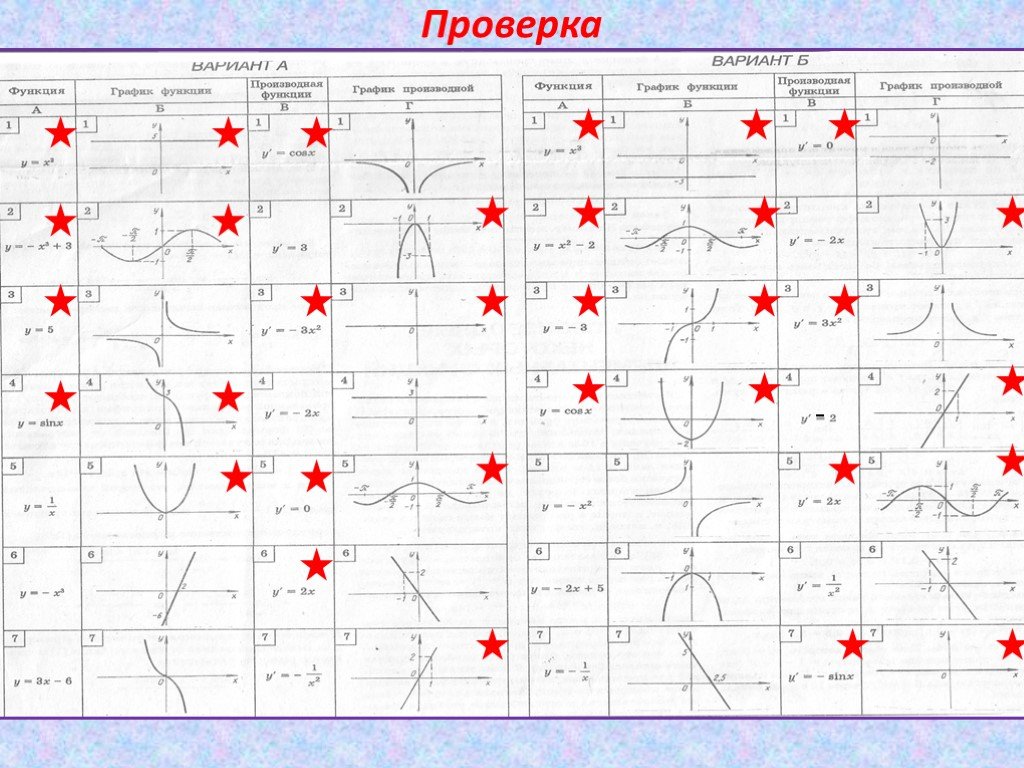
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько ...Практическое применение подобия треугольников
СКАЗКА ЛОЖЬ, ДА В НЕЙ НАМЕК…. Был День рождения Шрека и Фиона решила отметить его несколько необычно. После долгого рабочего дня, Шрек пришёл домой ...Применение производной
Функция НЕ функция. у а б 2 Графики функций. . Возрастание и убывание функции. Иду в гору. Функция возрастает на промежутке[b;a]. Иду под гору. Функция ...Практическое применение подобия треугольников
Подобие в жизни. Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. ...Практическое применение подобия треугольников
Цель урока:. Закрепить понятие подобия треугольников Узнать где применяется подобие в жизни Рассмотреть решение задач на местности. Понятие подобия ...Практическое применение геометрии
1. Выяснить области применения геометрии в целом. 2. Выяснить области применения теоремы Пифагора. Цель:. Применение геометрии в развед.целях. Измерение ...Практическое применение логарифмов в экономике
Непер Джон (1550 - 1617) Известный английский математик, шотландский барон. Математика и астрономия были его увлечениями, а не профессией. Непер вошел ...Применение производной к исследованию функций
Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики. Готфрид Вильгельм фон Лейбниц. ...Применение производной к исследованию функций
Цель урока – закрепить и систематизировать знания учащихся по исследованию функций с помощью производной. Применение производной к исследованию функции. ...Применение производной к исследованию функций
Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, и умение. ...Применение производной к исследованию и построению графиков функций
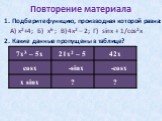
Цель урока:. научиться применять таблицу производных при исследовании функций и построении графиков. Математический диктант. Вариант 1. (Cu)’=… …=(u’v-v’u)/v² ...Применение производной к исследованию функции
Применение производной к исследованию функции. Критические точки функции. х у у = g (х) у = f (х). Повторение: описание свойств функции по её графику ...Применение производной для исследования функции на монотонность и экстремумы
Х У 0 касательная α. k – угловой коэффициент прямой (касательной). Геометрический смысл производной: если к графику функции y = f(x) в точке с абсциссой ...Применение производной для исследования функций
Монотонность функции. Убывает на (-;x, x) Возрастает на х1; х2. Постоянна на а;в. у х У=f(x) x1 а в. Исследование функции на возрастание. ...Применение производной в различных областях науки
Первый корпус БелГУ. с. Ливенка 2012год. Урок – деловая игра по теме: «Применение производной в различных областях науки». Корнева Г.Н., учитель математики, ...Интеграл и его практическое применение
Выполнил: Ершов Николай, ученик 11 класса. Руководитель: Дедовец Надежда Артемовна, учитель математики. С. Большой Атлым 2012-2013 уч. год. Цель работы: ...Применение производной функции
с и л а. в у м е. I вариант II вариант Буква С Буква В. Буква И Буква У. Буква Л Буква М. Буква А Буква Е 7. Сложилась фраза. ...Масштаб и его практическое применение
Устный счет. 1 мм 1дм 1 км •10 •1000 1 м :1000 :10 1 см М е р ы д л и н ы. 7. 6. 5. 3. 2. 1. 2 м 64 см меньше, чем 300 см. Неверно, что 1 м = 10 дм. ...Применение производной в физике
В математике следует помнить не формулы, а процессы мышления. В.П. Ермаков. Урок № 1 повторительно-обобщающий. Производная и ее применение при решении ...Конспекты
Применение производной для решения задач экономического содержания
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 31. города Мурманска. конспект урока. «Применение ...Применение производной к исследованию свойств функции и к решению прикладных задач
Конспект урока алгебры для учащихся 10 класса. Тема урока:. Применение производной к исследованию свойств функции и к решению прикладных задач. ...Геометрическое применение производной
Тема «Геометрическое применение производной». Производная функции y = y(x) при данном значении аргумента х = х. 0. равна угловому коэффициенту касательной, ...Геометрический смысл производной. Применение производной к исследованию функций
Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций». Цель урока. :. содействовать созданию ...Применение производной для решения задач
5. . Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Рузаевского района Республики Мордовия. ...Геометрический и физический смысл производной. Применение производной
Учитель математики. КГУ «Экономический лицей». Воробьева. Ирина. Юрьевна. Методическая разработка. урока математики в 10 классе. « Геометрический ...Применение производной для исследования функций на монотонность и экстремумы
Урок алгебры в 10 классе. по теме: «Применение производной для исследования функций. . на монотонность и экстремумы». Тип урока:. . интегрированный. ...Производные функций и применение производной
Государственное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа с. Чёрный Ключ. . муниципального района Клявлинский ...Масштаб: практическое применение
Урок с использованием презентации. Автор: Герасимова Светлана Николаевна (. sn.qer@mail.ru. ). Место работы: муниципальное нетиповое общеобразовательное ...Масштаб и его практическое применение
Урок в 5-м классе по теме "Масштаб и его практическое применение". . Панфилова Ольга Юрьевна. учитель математики. . . Цели:. . . формировать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:18 ноября 2018
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию