Презентация "Применение производной для исследования функций" по математике – проект, доклад
Презентацию на тему "Применение производной для исследования функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
«Применение производной для исследования функции»
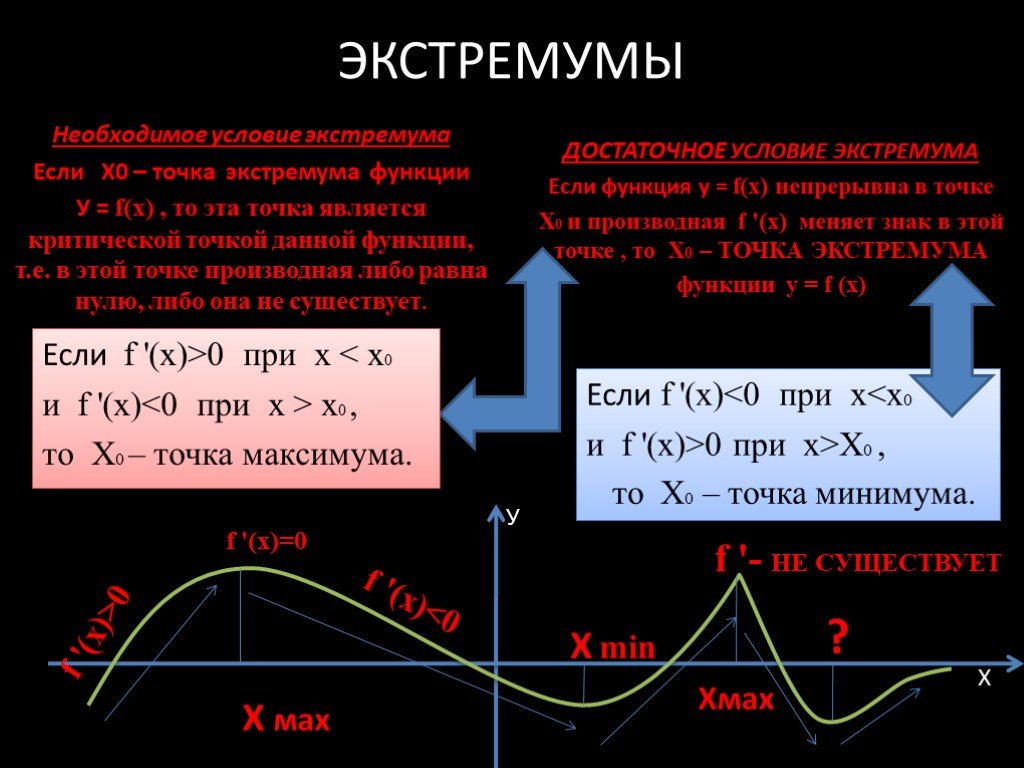
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько ...Применение производной
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце 17 столетия. Тем более поразительно, что за долго до этого ...Применение производной
Творческое название Гимн производной. Флюксия! Слово прекрасное, может, волшебное? Флюксия! Петь даже хочется что-то душевное. Флюксия! Точки экстремума: ...Применение ИКТ для подготовки к ЕГЭ по математике
«Тот, кто не смотрит вперед, оказывается позади» Джордж Герберт. Повышение эффективности работы педагога при подготовке учащихся к сдаче ЕГЭ по математике. ...Применение производной
Функция НЕ функция. у а б 2 Графики функций. . Возрастание и убывание функции. Иду в гору. Функция возрастает на промежутке[b;a]. Иду под гору. Функция ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Практическое применение производной
ОБУЧАЮЩАЯ :. повторить, обобщить, систематизировать знания по данной теме ; показать учащимся необходимость знания материала изученной темы при решении ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Построение графиков функций
1. Находить особо важные точки графика: - стационарные и критические точки; - точки экстремума; - точки пересечения графика с осями координат; - точки ...Понятие производной
Сегодня у нас праздник! Эпиграф: Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. А.Поуп. Что такое высшая математика? Когда ...Общие свойства функций
Вариант 1 Вариант 2 Задача 1. Найти область определения функции. Задача 2. Функция f(x) возрастающая. Сравните f(3) и f(5). Функция f(x) убывающая. ...Аппроксимация функций
Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции. Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени ...Применение задач линейного программирования в практической деятельности
Если ученик в школе не научился сам ничего творить, то и в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы, научившись ...Внеклассное мероприятие по математике для 8 класса Отличники
1. Способствование проявлению интеллектуальных способностей учащихся. 2. Активизации познавательной деятельности учащихся. 3. Формирование навыков ...Викторина по математике для 5-6 классов
1.Половина-треть числа. Какое это число? Ответ: 3/2. 2.За книгу заплатили 60 рублей. И ещё 1/3 стоимости книги. Сколько стоит книга? 90 рублей. 3.Как ...Виды функций
План. Величины постоянные и переменные Понятие функции: определение функции область определения, значения сложная функция способы задания функции ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Вводное повторени для 8 классов по геометрии
8 9 10 11 14 15 16 17 18 30 33 34 35 36 1 3 4 5 6 13 19 31 7. Найти: 440 D С О В А ? 2. Дано:. a0 F b0. O. N R M L. a b c 650. . 450 K E 1350 800. ...Конспекты
Применение производной для исследования функций на монотонность и экстремумы
Открытый урок по математике в 10 классе по теме:. «Применение производной для исследования функций на монотонность и экстремумы». Цели и задачи:. ...Применение производной для исследования функций на монотонность и экстремумы
Урок алгебры в 10 классе. по теме: «Применение производной для исследования функций. . на монотонность и экстремумы». Тип урока:. . интегрированный. ...Применение производной для решения задач
5. . Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Рузаевского района Республики Мордовия. ...Применение производной к исследованию функций и построению графиков
ОГБОУ СПО «Белгородский строительный колледж». Конспект урока по дисциплине. «Математика». Тема: «Применение производной к ...Применение производной для решения задач экономического содержания
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 31. города Мурманска. конспект урока. «Применение ...Применение производной к исследованию функций. Наибольшее и наименьшее значение функции
ГОУ «Школа здоровья и индивидуального развития». Красногвардейского района. Санкт-Петербурга. Урок алгебры и начал анализа. ...Применение производной к построению графиков функций
Применение производной к построению графиков функций. Алгебра и начала анализа 11 класс. Автор: Димакова Ольга Николаевна – учитель математики ...Производные функций и применение производной
Государственное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа с. Чёрный Ключ. . муниципального района Клявлинский ...Геометрический смысл производной. Применение производной к исследованию функций
Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций». Цель урока. :. содействовать созданию ...Применение метода интервалов для решения неравенств
Применение метода интервалов для решения неравенств. . . 9-й класс. Цель урока:. рассмотреть применение метода интервалов для решения неравенств ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 марта 2019
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию