Презентация "Аппроксимация функций" по математике – проект, доклад
Презентацию на тему "Аппроксимация функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Преобразования графиков функций
A B C x y 0 1. В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2). ...Преобразование графиков функций
Дорогу осилит идущий, а математику – мыслящий Т.Эдисон. Цель урока. Изучить способ построения графиков функций y = f(kx), y = mf(x). Преобразование: ...Преобразование графиков функций, содержащих модуль
y = f(x) + a y = f(x) y = f(x) - a +a -a. Преобразование графиков функций. Т1. Параллельный перенос по оси Оу. y = f(x) график исходной функции. y ...Свойства функций
Обобщить и систематизировать знания по теме «Исследование функций». 1.Повторить схему исследования функции. 2.Развивать умение применять теоретические ...Функции. Графики функций
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа. 2. Функция задана формулой Найдите её значение при х = 2. 3. ...Свойства производной. Построение графиков функций
Построение графика функции, заданной формулой, начинают с её исследования 1) Находят область определения функции 2) Выясняют, является ли функция ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Готовимся к ОГЭ – 2018 Задание 23 Графики функций
Цель урока: подготовка к ОГЭ; отработка умений решать задачи, связанные с построением графиков различных функций. Постройте график функции и определите, ...Виды функций
План. Величины постоянные и переменные Понятие функции: определение функции область определения, значения сложная функция способы задания функции ...Возрастание и убывание функций
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на отрезке [-1;10]. Эта функция ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Применение производной к исследованию функций
Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, и умение. ...Графики квадратичных функций
Этапы рассмотрения Простейшие примеры Свойства графиков квадратичных функций Графики и коэффициенты уравнений – простейшие закономерности Динамические ...Применения производной к исследованию функций
Оглавление. Схема исследования функций; Признак возрастания (убывания) функции: Достаточный признак возрастания функции; Достаточный признак убывания ...Графики простейших функций, содержащих модули
Графики простейших функций, содержащих модули. Определение модуля:. Модулем числа х называется расстояние от начала отсчета до точки, изображающей ...Решение задач на построение графиков алгебраических функций
Анализ содержания материала. Кто не знает в какую гавань он плывет, для того нет попутного ветра. Сенека. Главной целью данной темы является: научить ...Графики тригонометрических функций
тригонометрические функции. Графиком функции у = sin x является синусоида. Свойства функции: D(y) =R Периодическая (Т=2p) Нечетная (sin(-x)=-sin x) ...Конспекты
Преобразование графиков тригонометрических функций
Конспект урока по алгебре в 10 классе. Васильева Екатерина Сергеевна. ,. . учитель математики. ОГБОУ «Смоленская специальная (коррекционная). ...Применение производной для исследования функций на монотонность и экстремумы
Открытый урок по математике в 10 классе по теме:. «Применение производной для исследования функций на монотонность и экстремумы». Цели и задачи:. ...Взаимное расположение графиков линейных функций
Учитель: Короленко Евгения Николаевна. Конспект урока по алгебре 7 класса. Тема «Взаимное расположение графиков линейных функций». Цели:. Образовательные:. ...Преобразование графиков тригонометрических функций
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Свойства функций
Тема урока:. Свойства функций. Предварительная подготовка к уроку:. обучающиеся должны знать следующие темы: «Линейная функция и ее график», «Обратная ...Свойства функций. Чтение графиков функций
Муниципальное бюджетное образовательное учреждение «Усть – Вельская СОШ № 23». Свойства функций. Чтение графиков функций. Конспект урока по алгебре. ...Взаимное расположение графиков линейных функций
ПЛАН-КОНСПЕКТ УРОКА Конспект урока по теме: «Взаимное расположение графиков линейных функций». . ФИО (полностью). . Чичерова Татьяна ...Распознавание графиков линейной, квадратичной функций и обратной пропорциональности
МБОУ «Кимовская средняя общеобразовательная школа Спасского муниципального района РТ». Урок по алгебре в 9 классе на тему. «Распознавание ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Взаимное расположение графиков линейных функций
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:2 мая 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию





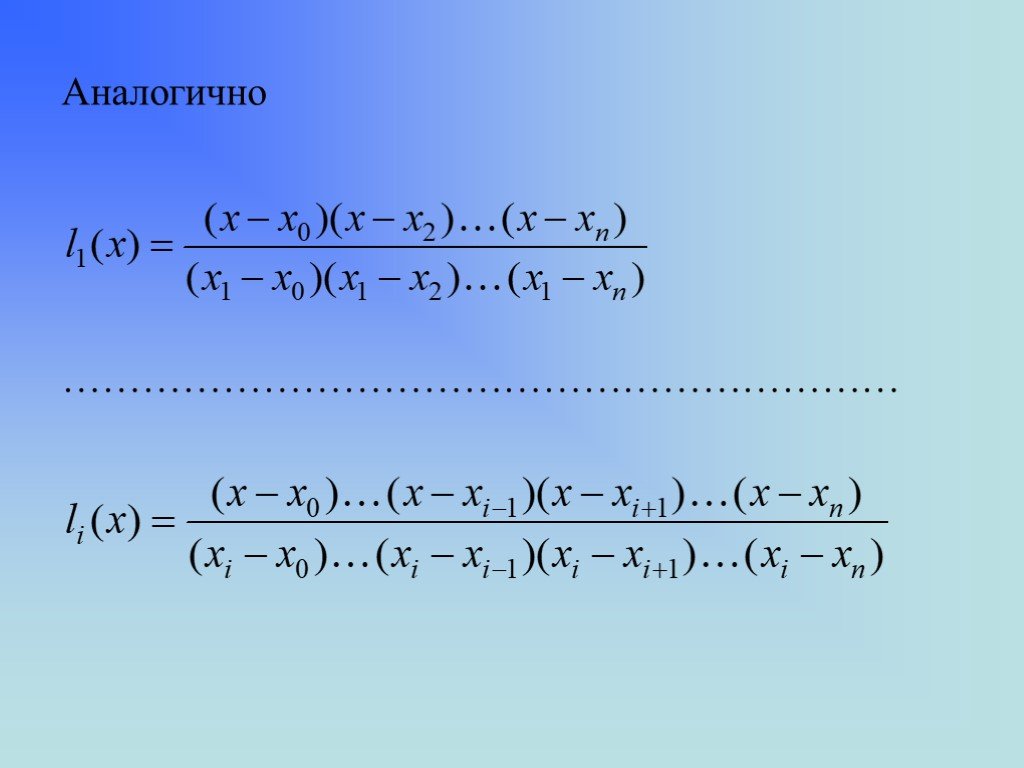













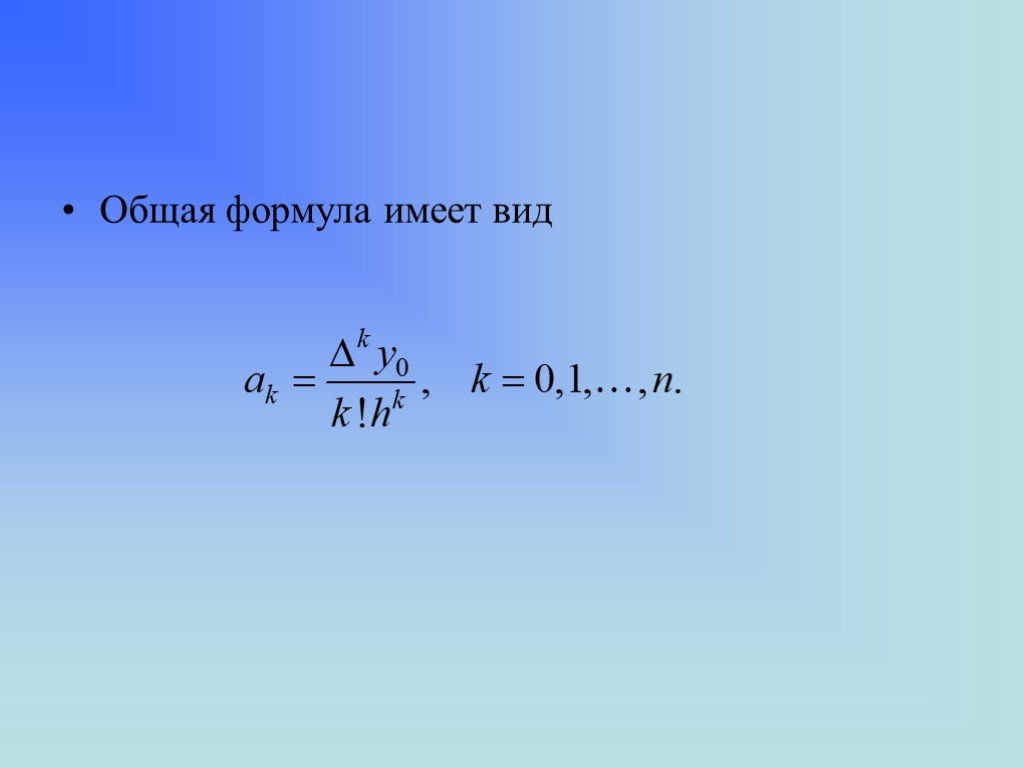



























![Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента [х0, хn]. Однако с точки зрения повышения точности расчетов более целесообразно использовать эту формулу для вычисления значении функции в точках левой половины рассматриваемого отрезка. Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента [х0, хn]. Однако с точки зрения повышения точности расчетов более целесообразно использовать эту формулу для вычисления значении функции в точках левой половины рассматриваемого отрезка.](https://prezentacii.org/upload/cloud/19/05/143937/images/thumbs/screen23.jpg)
![Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае](https://prezentacii.org/upload/cloud/19/05/143937/images/thumbs/screen24.jpg)