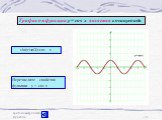
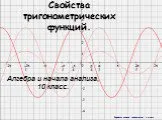
Презентация "Графики тригонометрических функций" по математике – проект, доклад
Презентацию на тему "Графики тригонометрических функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
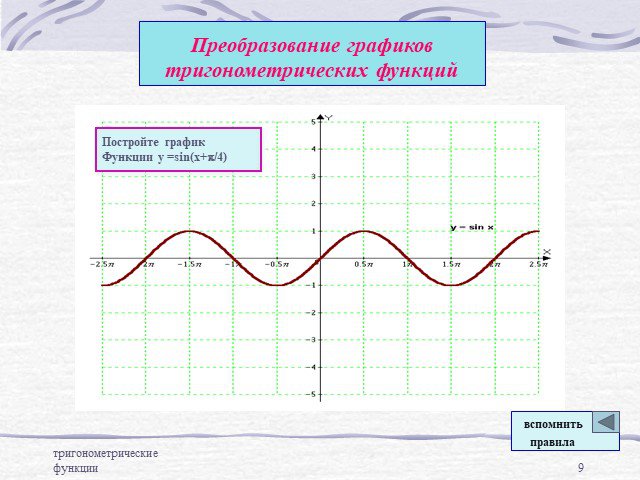
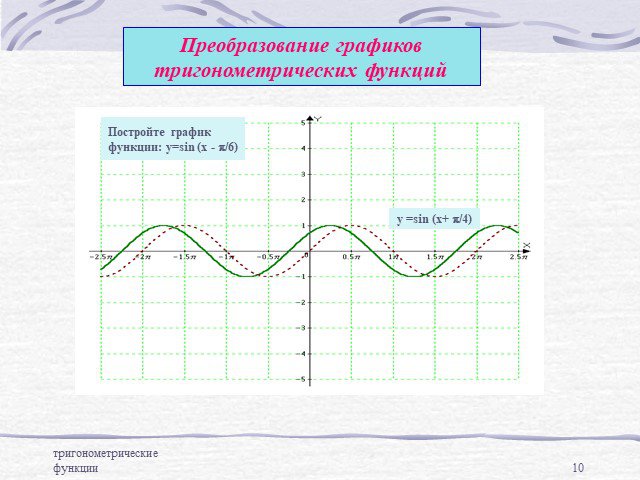
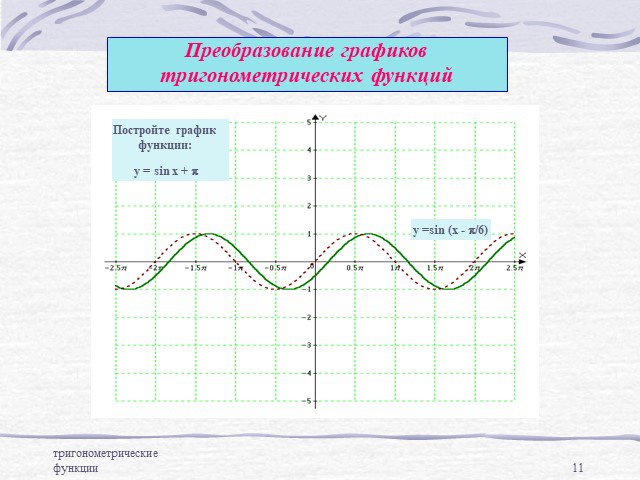
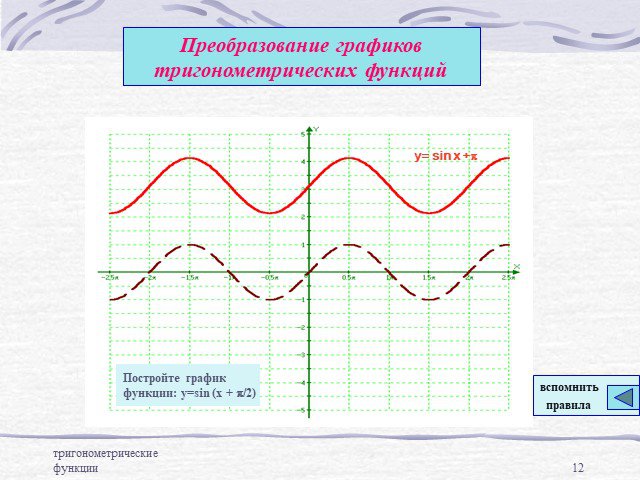
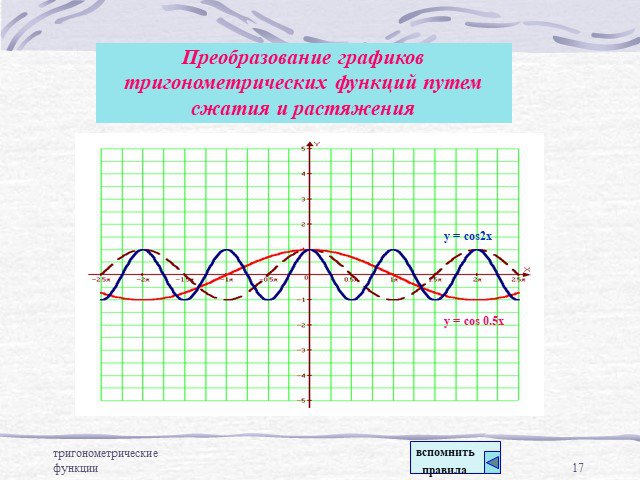
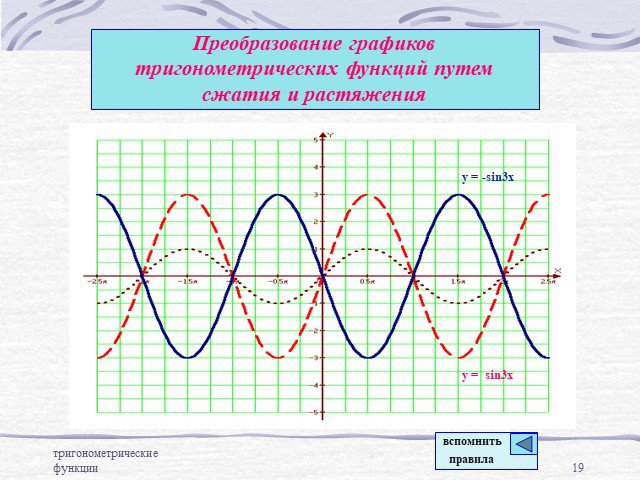
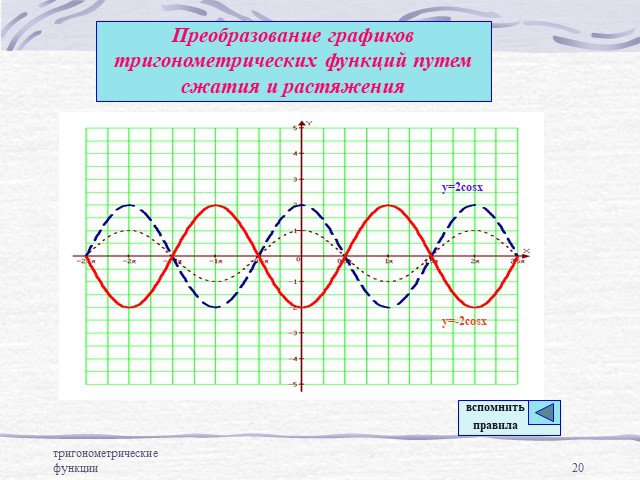
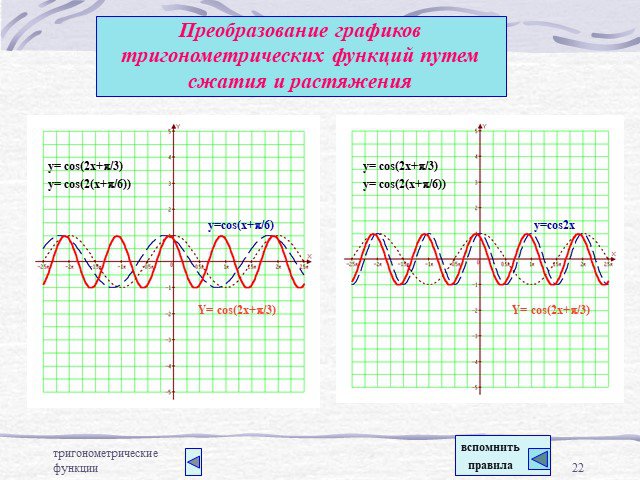
Преобразование графиков тригонометрических функций
Цели урока:. Обобщить и систематизировать знания учащихся по теме. Показать актуальность темы в связи с введением ЕГЭ в штатный режим. Показать возможности ...Преобразование графиков тригонометрических функций
Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в положительном направлении ...Преобразование графиков тригонометрических функций
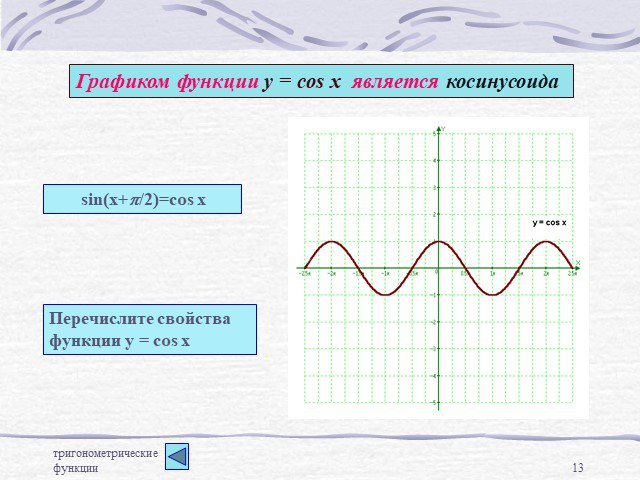
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Преобразование графиков тригонометрических функций
Цель урока:. Повторить свойства тригонометрических функций Изучить графическую программу Advanced Grapher, облегчающую построение графиков Изучить ...Преобразование графиков тригонометрических функций
Оборудование урока: компьютер, проектор, экран. Цели: Обобщить знания и умения. Развить умение наблюдать, сравнить, обобщать. Воспитать познавательную ...Свойства тригонометрических функций
I. Свойства функции y=sinx. x 1 0 Масштаб :3 −1 y. 1) Область определения функции – любые числа (x);. 2) Область значений функции – отрезок от ...Свойства тригонометрических функций
Сегодня на уроке я приглашаю вас посетить «Математическое кафе». Каждой паре предлагается сесть за отдельный столик (девушка и парень). Всем посетителям ...Свойства обратных тригонометрических функций
Тема элективного занятия: «ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ. РЕШЕНИЕ УРАВНЕНИЙ, СОДЕРЖАЩИХ АРКФУНКЦИИ». ЦЕЛИ УРОКА: 1. Обобщить, систематизировать ...Готовимся к ОГЭ – 2018 Задание 23 Графики функций
Цель урока: подготовка к ОГЭ; отработка умений решать задачи, связанные с построением графиков различных функций. Постройте график функции и определите, ...Нахождение значений тригонометрических функций с помощью таблиц Брадиса
Четырёхзначные таблицы В.М. Брадиса. Владимир Модестович Брадис - математик, педагог. Родился 23 декабря 1890 года в семье учителей начальной школы ...Функции. Графики функций
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа. 2. Функция задана формулой Найдите её значение при х = 2. 3. ...Свойства и графики элементарных функций
1. Определение функции. 2. Линейная функция: возрастающая; убывающая; частные случаи. 3. Квадратичная функция. 4. Степенная функция: с четным натуральным ...Построение графиков тригонометрических функций
формирование знаний и умений преобразовать графики тригонометрических функций. Цель:. Закрепить применение программы MS Excel для построения графиков ...Графики квадратичных функций
Этапы рассмотрения Простейшие примеры Свойства графиков квадратичных функций Графики и коэффициенты уравнений – простейшие закономерности Динамические ...Производная и графики функций
Доказать, что функция монотонна на заданном промежутке:. Дана непрерывная на функция. Используя график производной этой функции, определите, имеет ...Свойства функций и их графики
Повторение по теме: «Свойства функций и их графики». 1. Что такое функция? 2. Как можно задать функцию? Определение. «Зависимость переменной y от ...Графики функций
Проверка знаний учащихся по теме «Графики функций и уравнений». Проверочный тест Упражнение «Подумай и выбери!» Творческое задание. +. «Глядя на мир ...Графики функций с модулями
Цель работы:. Научится строить графики функций с модулями. Хорошая подготовка к ЕГЭ. 1 ФУНКЦИЯ С МОДУЛЕМ. Y=lXl Строим график функции у = x Из-за ...Графики функций
План урока:. Линейная функция Прямая пропорциональность Взаимное расположение графиков линейных функций Практикум. Линейная функция. Что такое линейная ...Квадратичная функция. Графики функций
Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании Аристотель. Устный опрос Сформулировать определение квадратичной ...Конспекты
Преобразование графиков тригонометрических функций
Конспект урока по алгебре в 10 классе. Васильева Екатерина Сергеевна. ,. . учитель математики. ОГБОУ «Смоленская специальная (коррекционная). ...Свойства тригонометрических функций
Тема: Свойства тригонометрических функций. Цель:. Повторить, закрепить, обобщить свойства тригонометрических функций. Совершенствовать умения и ...Преобразование графиков тригонометрических функций
. . Воробьева Ирина Юрьевна. учитель математики. 1 категории. ГУ «Экономический лицей». г. Семей. Методическая разработка урока. ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Нахождение значений тригонометрических функций от аркфункций
Муниципальное бюджетное общеобразовательное учреждение. «Тиксинская средняя общеобразовательная школа №2». Разработка ...Преобразование графиков тригонометрических функций
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Графики функций и их производных
МОУ Карагайская СОШ. (итоговое повторение). Учитель математики и информатики: Бурдова И.К. ЦЕЛИ УРОКА. :. . ...Экскурс в мир тригонометрических функций
Славенко Н. В. МОУ СОШ № 32 г. . г Братск. . . Урок обобщающего повторения в 11 классе. . «Экскурс в мир тригонометрических функций». . ...Графики функций y=ах2+n и y=а(х-m)2
МБОУ СОШ№49г .Шахты. Ростовской области. . Конспект урока алгебры. в 9 классе. на тему. «. Графики функций. y. =ах. 2. +. n. и. y. ...Графики функций y = ax2+ n и y = a(x-m)2
Тема:. «Графики функций y = ax2+ n и y = a(x-m)2». Цели:. формирование умений строить график квадратичной функции (частные случаи), определять ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:неизвестен
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию


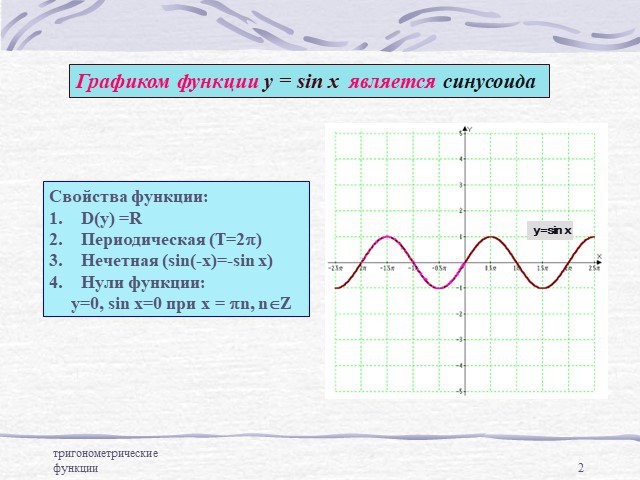
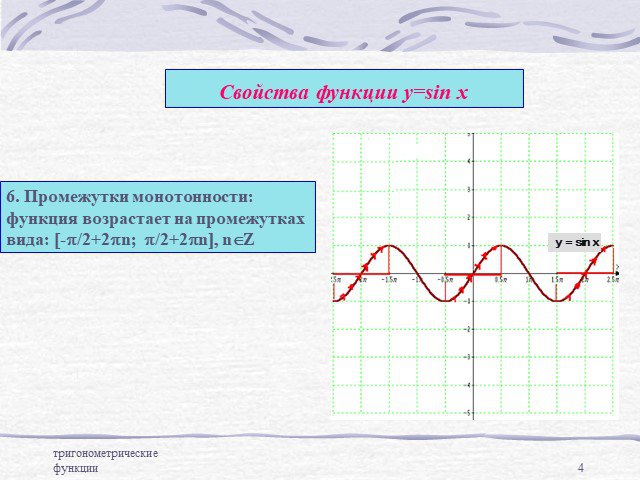









![Свойства функции у=sin x. 6. Промежутки монотонности: функция возрастает на промежутках вида: [-p/2+2pn; p/2+2pn], nÎZ Свойства функции у=sin x. 6. Промежутки монотонности: функция возрастает на промежутках вида: [-p/2+2pn; p/2+2pn], nÎZ](https://prezentacii.org/upload/cloud/14/09/6136/images/thumbs/screen4.jpg)
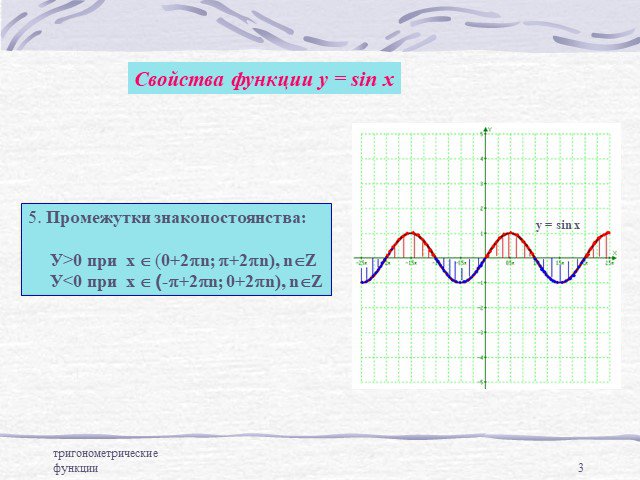
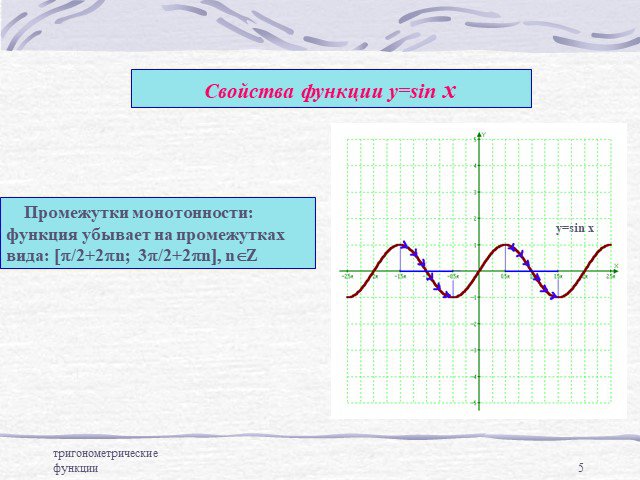
![Промежутки монотонности: функция убывает на промежутках вида: [p/2+2pn; 3p/2+2pn], nÎZ Промежутки монотонности: функция убывает на промежутках вида: [p/2+2pn; 3p/2+2pn], nÎZ](https://prezentacii.org/upload/cloud/14/09/6136/images/thumbs/screen5.jpg)

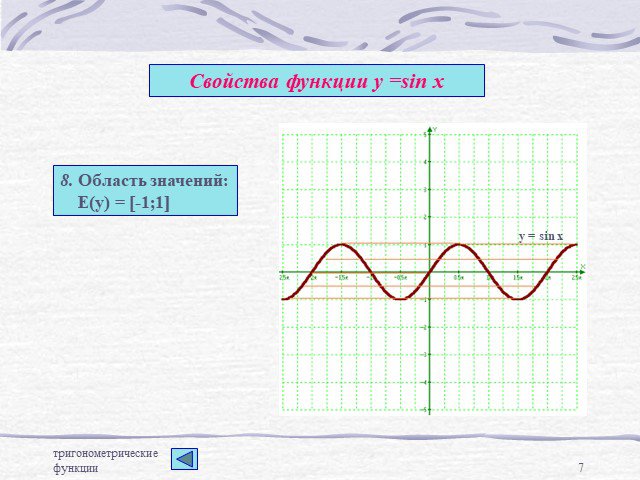
![8. Область значений: Е(у) = [-1;1] 8. Область значений: Е(у) = [-1;1]](https://prezentacii.org/upload/cloud/14/09/6136/images/thumbs/screen7.jpg)