Конспект урока «Преобразование графиков тригонометрических функций» по математике для 10 класса
Математику уже затем следует учить, что она ум в порядок приводит.
М. В. Ломоносов.
Урок математики (продолжительность 1ч 20мин)
| Преобразование графиков тригонометрических функций | |
| Цели: Образовательная | Дать понятие числовой функции, области определения функции, области значений, определения объединения множеств (используется для записи области определения и значений) Выучить определение целой рациональной функции, дробно-рациональной функции, научить преобразовывать графики функций |
| Развивающая | Развивать логическое мышление, умение применять полученные знания на практике, при решении конкретных задач |
| Воспитательная | Воспитывать интерес к предмету, любознательность, прививать культуру поведение на уроке |
| Оборудование | Персональные компьютеры, интерактивная доска, письменные принадлежности для построения графиков в тетрадях, учебник «Алгебра и начала анализа», под ред. А.Н. Колмогорова |
Ход урока
-
Организационный момент (5мин)
Примечание
Для того, чтобы настроить учащихся на умственную деятельность, дать им собраться, часто на своих уроках применяю следующую разминку.
«Фронтальный опрос».
-
Какой сегодня день?
-
Сколько времен года вы знаете?
-
Какое сейчас время года?
-
В каком веке жил А,С. Пушкин?
-
Какие материки омывает Индийский океан?
-
Назовите столицу Франции
-
В каком полушарии находится Антарктида?
-
Если у нас зима, то в Австралии что?
-
Сколько сантиметров в метре?
-
Водород это металл или неметалл?
-
Назовите стороны света
-
Назовите третью планету от Солнца
-
Целеполагание и мотивация. (2 мин)
Объявление темы урока
Сегодня на уроке мы научимся преобразовывать графики тригонометрических функций. Чтобы не тратить много времени на вычисления значений функций и построения самих графиков будем использовать табличный редактор Excel.
-
Повторение и проверка домашнего задания: (10мин)
-
Фронтальный опрос:
-
-
Что представляет собой единичная окружность?
-
Назвать знаки синуса, косинуса, тангенса, котангенса на единичной окружности
-
Назвать четные и нечетные тригонометрические функции
-
Какая тригонометрическая функция является четной?
-
Назовите область определения и область значений тригонометрических функций.
-
Учащимся на компьютере предлагается пройти тест для проверки знания значений тригонометрических функций углов 0, 30, 45,60, 90, 180, 270, 360 градусов. После прохождения теста на доске предлагаются правильные ответы.
-
Изучение нового материала. (45мин)
-
Дать понятие числовой функции, области определения функции, области значений, определения объединения множеств (используется для записи области определения и значений)
-
Выучить определение целой рациональной функции, дробно-рациональной функции,
-
Решить пример на нахождение области определения дробно-рациональной функции (решение примера демонстрируется на интерактивной доске)
-
Преобразование графиков функций.
На доске показаны графики известных функций: линейной, квадратичной, обратной пропорциональности, тригонометрических.
-
Параллельный перенос графиков.
На доске приводится пример построения графика функции y=x2, y=x2+4, y=x2-6. Графики строятся в среде MS Excel.
Учащиеся должны сделать вывод:
Для построения графика функции y=f(x) + b, где b – константа, надо переместить график функции f вдоль оси ординат на вектор (0;b).
.
Совместно с учащимися построить с помощью табличного редактора графики функций y=sinx+2,
у=x2-5.
Последовательность действий:
1.В ячейки А1:Z1 ввести значения от -5 до 5 с шагом 0,4 с помощью автозаполнения,
2. В ячейкуА2 ввести формулу sinx+2, ссылаясь на значение х в ячейке А1. Скопировать формулу в В2:Z2.
3. Не убирая выделение ячеек, нажать кнопку вставки диаграммы, выбрать вид – точечная. Получим график:
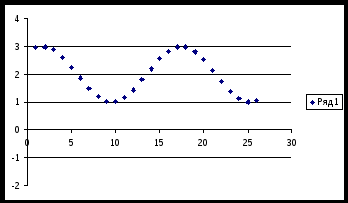
Аналогично строится график второй функции.
В тетрадь записывается область определения и область значений функций (используются построенные графики этих функций).
Построить графики №38 (в,г)
Физкультминутка. Выполнить упражнения для снятия напряжения, упражнения для глаз
-
Растяжение вдоль оси Оу с коэффициентом k.
Построить графики функций y=1/2sinx, y=2sinx.
Сделать выводы о растяжения графиков в зависимости от коэффициента (сжатие, растяжение).
Записать в тетради область определения и область значений функций
Построить самостоятельно графики функций № 37 (а,б,в,г).
-
Параллельный перенос вдоль оси абсцисс на вектор (а;0).
Построить графики функций № 33( а,б,в,г), 45(а). Сделать самостоятельно выводы, записать область определения и область значений функций.
-
Растяжение вдоль оси Ох с коэффициентом k.
Построить графики функций y=sinx, y=sin4x, y=sinx/4 в одной системе координат и y=cosx, y=cos3x, y=cos(x/2) – в другой Выбрать тип диаграммы – график.
Сделать самостоятельно выводы, записать область определения и область значений функций.
Самостоятельно построить графики функций y=sinx, y=sin2x, y=sin(x/2) в одной системе координат.
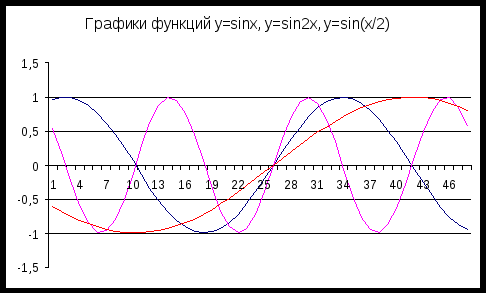
-
Закрепление материала.(10мин)
Построить самостоятельно графики функций № 45 (г), №18 (3.а, в), стр. 95; записать в тетрадь область определения и область значений функций.
-
Подведение итогов урока.(5 мин).
-
Домашнее задание (3мин). №36 (а,в), №37 (а,в)
Литература
Алгебра и начала анализа. Под ред. А.Н. Колмогорова. Просвещение, 2003. – 384с.
Здесь представлен конспект к уроку на тему «Преобразование графиков тригонометрических функций», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

