Презентация "Свойства биссектрисы угла" по математике – проект, доклад
Презентацию на тему "Свойства биссектрисы угла" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
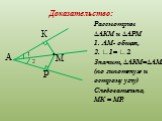
Свойство точек биссектрисы угла
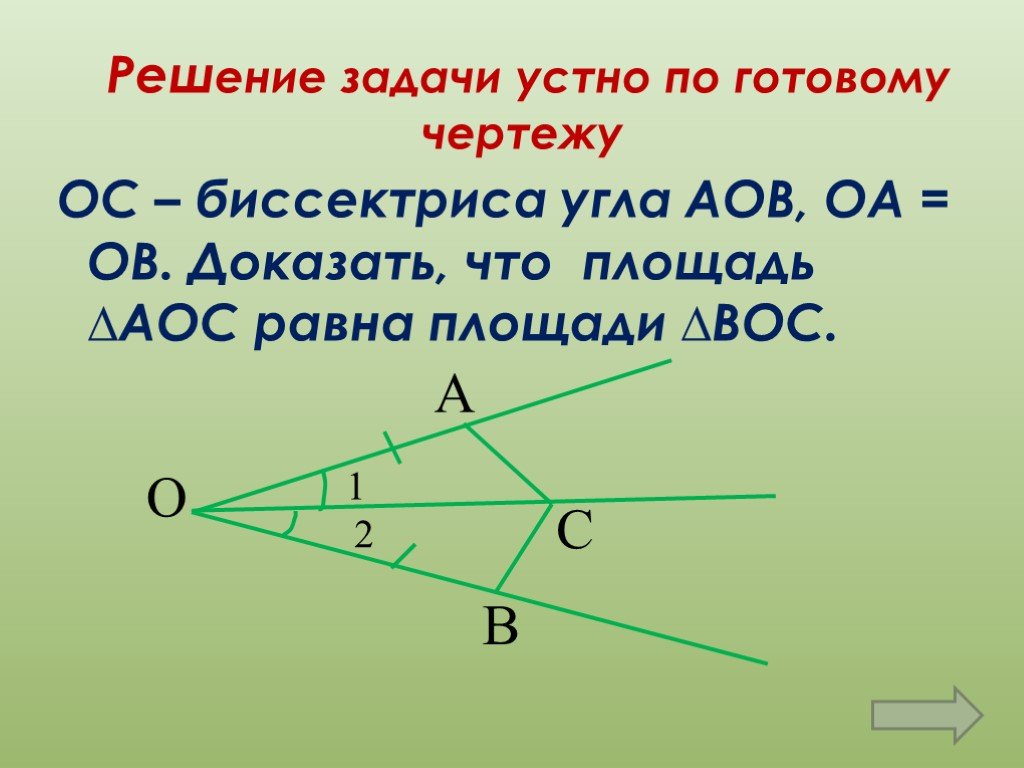
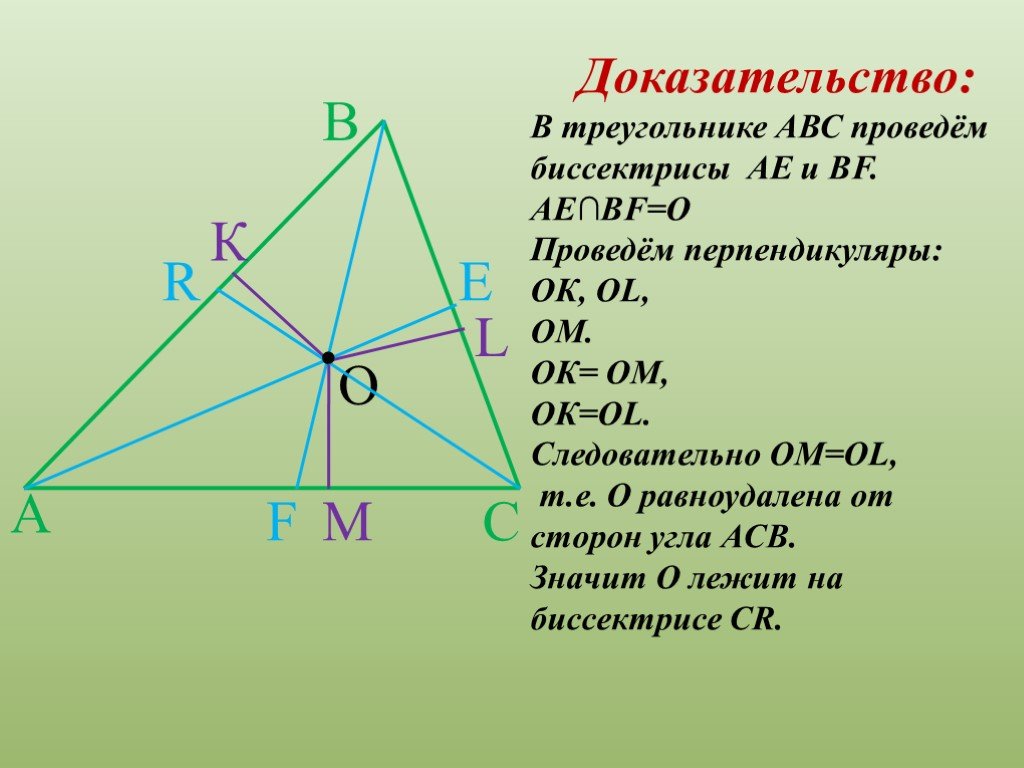
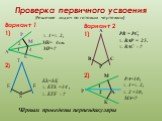
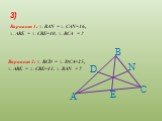
Основополагающий вопрос. - Как расположены точки биссектрисы угла от его сторон? - Какой фигурой будет геометрическое место точек, равноудалённых ...Свойство биссектрисы угла
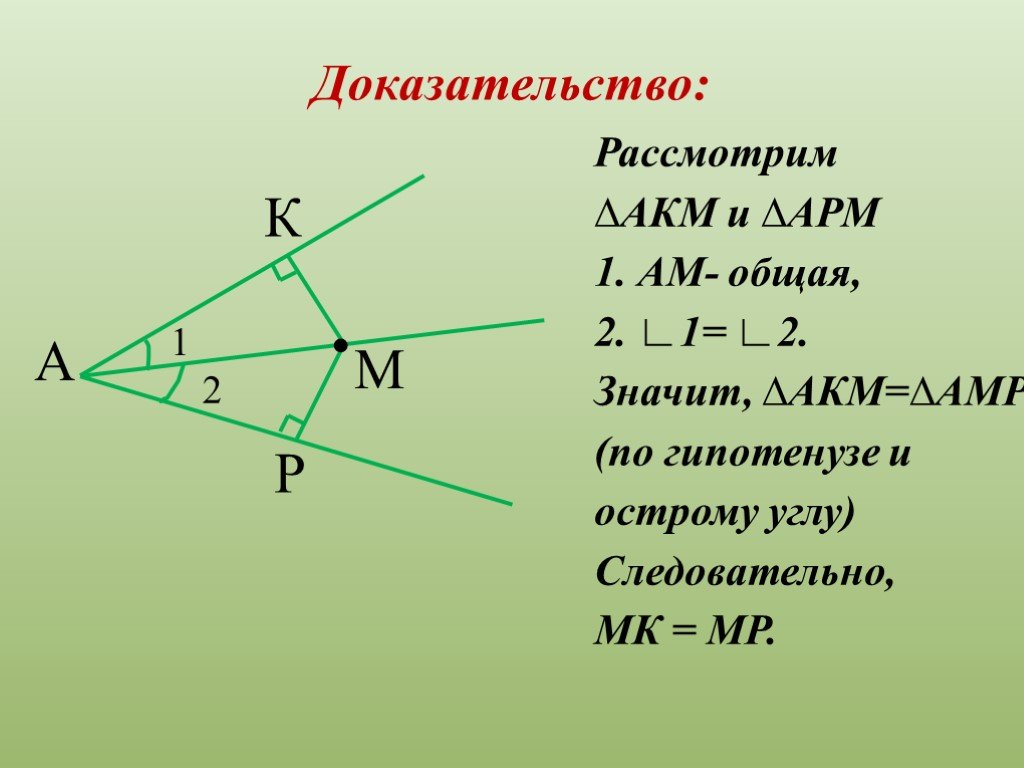
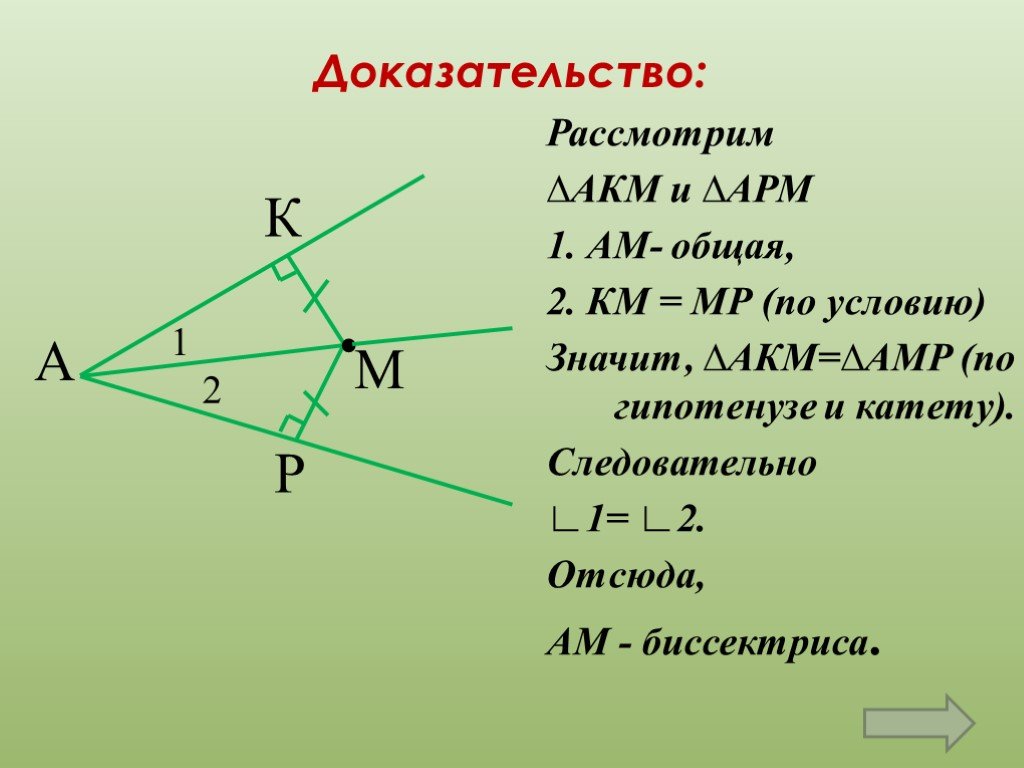
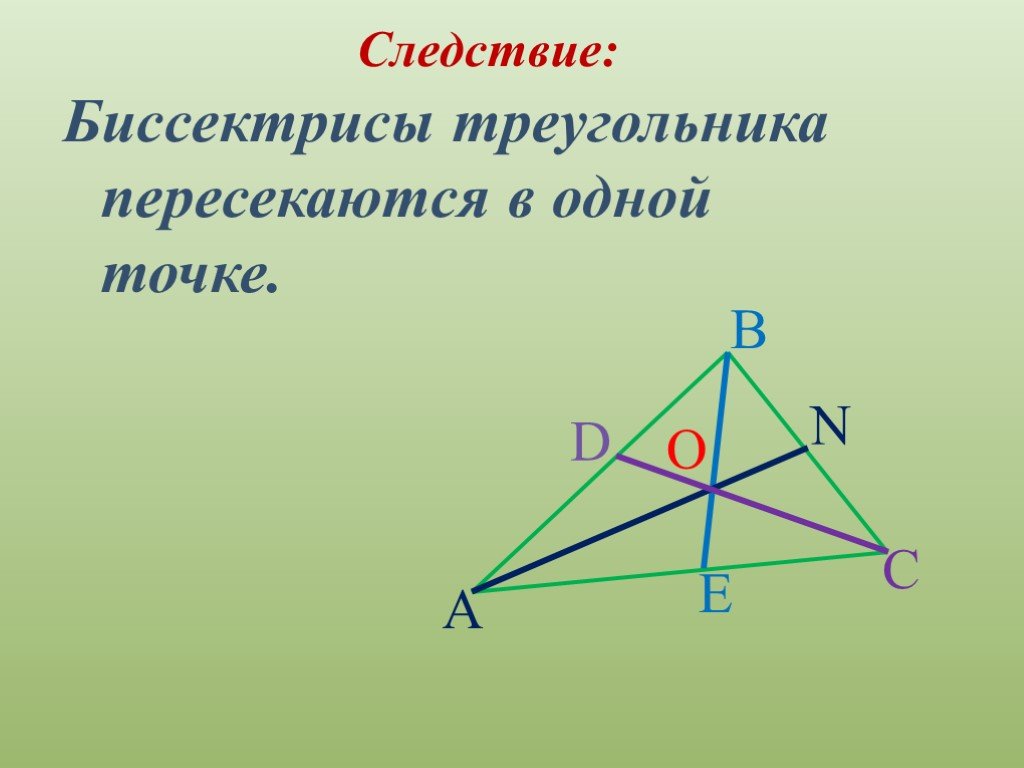
Цели урока:.Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Учить применять данные теоремы и следствие при решении задач. Формировать ...
Свойства прямоугольного параллелепипеда
Цели:. Определение прямоугольного параллелепипеда Измерения прямоугольного параллелепипеда Формулы для нахождения его квадрата диагонали Формула для ...Свойства функций
Обобщить и систематизировать знания по теме «Исследование функций». 1.Повторить схему исследования функции. 2.Развивать умение применять теоретические ...Свойство биссектрисы равнобедренного треугольника
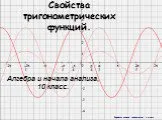
Повторение. Треугольник, у которого 2 стороны равны, называется равнобедренным треугольником. D С E B A C H M. DM – медиана треугольника АDВ. AM = ...Свойства тригонометрических функций
I. Свойства функции y=sinx. x 1 0 Масштаб :3 −1 y. 1) Область определения функции – любые числа (x);. 2) Область значений функции – отрезок от ...Свойства функции
Какой из графиков, изображенных на рисунках, задает функцию у=f(х). Почему? 1 3 4 х у. Продолжите предложение:. Говорят, что задана функция у=f(х) ...Свойства степеней
Вычислите, представьте в виде степени или упростите, если возможно. . . . Спасибо за то, что стараешься! ...Свойства степени с натуральным показателем
Квадратные уравнения. 1) х2 + 4x=0 2) х2 – 16 = 0 3) 3x2 + 10 = 0 4) 5x2 = 0 5) 2x2 – 7x = 0. Неполные квадратные уравнения. х2 + 4x=0 , х2 – 16 = ...Косинус острого угла прямоугольного треугольника
Историческая справка. Расположение углов и сторон. А С В b c a. АС – противолежащий катет. ВС – прилежащий катет. ВС - противолежащий катет. АС – ...Косинус угла
О В А С D. М N C. . Треугольник АВС – прямоугольный. ∟С – прямой. ∟А – острый. АС - прилежащий катет. ВС – противолежащий катет. АВ – гипотенуза. ...Задача о трисекции угла
Задача о трисекции угла разрешима при некоторых частных значениях величины данного угла. A C N M B D. При помощи циркуля и линейки можно разделить ...Знаменитые задачи древности. Трисекция угла
Выполнил: ученик 6 класса Зеленин Никита Руководитель: учитель математики Левищенко О. П. Образовательное учреждение: МОУ «Средняя общеобразовательная ...Зависимость между синусом, косинусом и тангенсом одного и того же угла
∙. . . П р о в е р ь и о ц е н и с е б я ! Ордината Абсцисса. О с н о в н о е т р и г о н о м е т р и ч е с к о е т о ж д е с т в о :. a2-b2=(a-b) ...Величина двугранного угла
?. ПОВТОРЕНИЕ ( устная работа). 1) Что называется углом на плоскости? 2) Какой угол называется углом между прямыми в пространстве? 3) Какой угол называется ...Биссектриса угла в треугольнике
Задачи УЧЕБНИК А О В С D 80º ? 180º- 80º= 100º 100º Ответ:155º, 25º, 155º. Задача №535 биссектриса ? Определение. Биссектриса угла – это луч с началом ...Свойства равнобедренного треугольника
Тема: «Свойства равнобедренного треугольника». Геометрия – это искусство хорошо рассуждать ... Нильс Г. Абель. Цели урока:. Создать условия для: введения ...Логарифмы. Свойства логарифма
ЛОГАРИФМЫ. Во многих задачах требуется уметь решать уравнения вида a =b. Для этого надо найти показатель степени по данным значениям степени и её ...Свойства сложения
26 октября. Классная работа. Цель: Знакомство со свойствами сложения (переместительным и сочетательным). Совершенствовать вычислительные навыки и ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Конспекты
Свойства степени с натуральным показателем
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 21. город Ставрополь. Конспект ...Свойства степени с натуральным показателем
Муниципальное общеобразовательное учреждение. гимназия № 4 г. Лыткарино. Конспект урока по алгебрев 7 классе«Свойства степени с натуральным ...Свойства сложения. Закрепление
7. . Урок-игра по математике во 2-м классе на тему. "Свойства сложения. Закрепление". Аджимефаева Алиме Решатовна, учитель начальных классов. ...Свойства степени с натуральным показателем
Технологическая карта открытого урока алгебры в 7 классе. УМК: А.Г. Мордкович . Алгебра: учебник для 7 класса общеобразовательных учреждений. ...Трапеция. Свойства трапеции
МБОУ гимназия № 12. . Ахонен Екатерина Петровна. . Геометрия. . 8 класс. . . Профильный уровень, используемые учебники: Геометрия: ...Число 0, цифра 0. Свойства нуля
12.12.08. Математика 1 класс. Петрова О.Н. ТЕМА: Число 0, цифра 0. Свойства нуля. ОСНОВНЫЕ ЦЕЛИ:. Сформировать представление о числе 0 ...Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Справочные сведения. Логарифмом. . положительного числа b. по основанию ...Свойства функций
Конспект урока по алгебре и началам анализа в 11 классе. . . . Учитель математики высшей категории. Юдинцева Валентина ...Квадрат. Прямоугольник. Свойства квадрата и прямоугольника. Решение геометрических задач. Проект «Оригами
Муниципальное бюджетное образовательное учреждение. «Основная общеобразовательная школа № 30». Конспект урока по математике во 2 классе. . ...Квадратные уравнения. Свойства коэффициентов
Технологическая карта урока математики. Учитель: Раковская Татьяна Ивановна. УМК: Алгебра 8 класс, авторы: Ю.Н. Мордкович, Н.Г. Мюндю, К.И. Пешков, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 октября 2018
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию