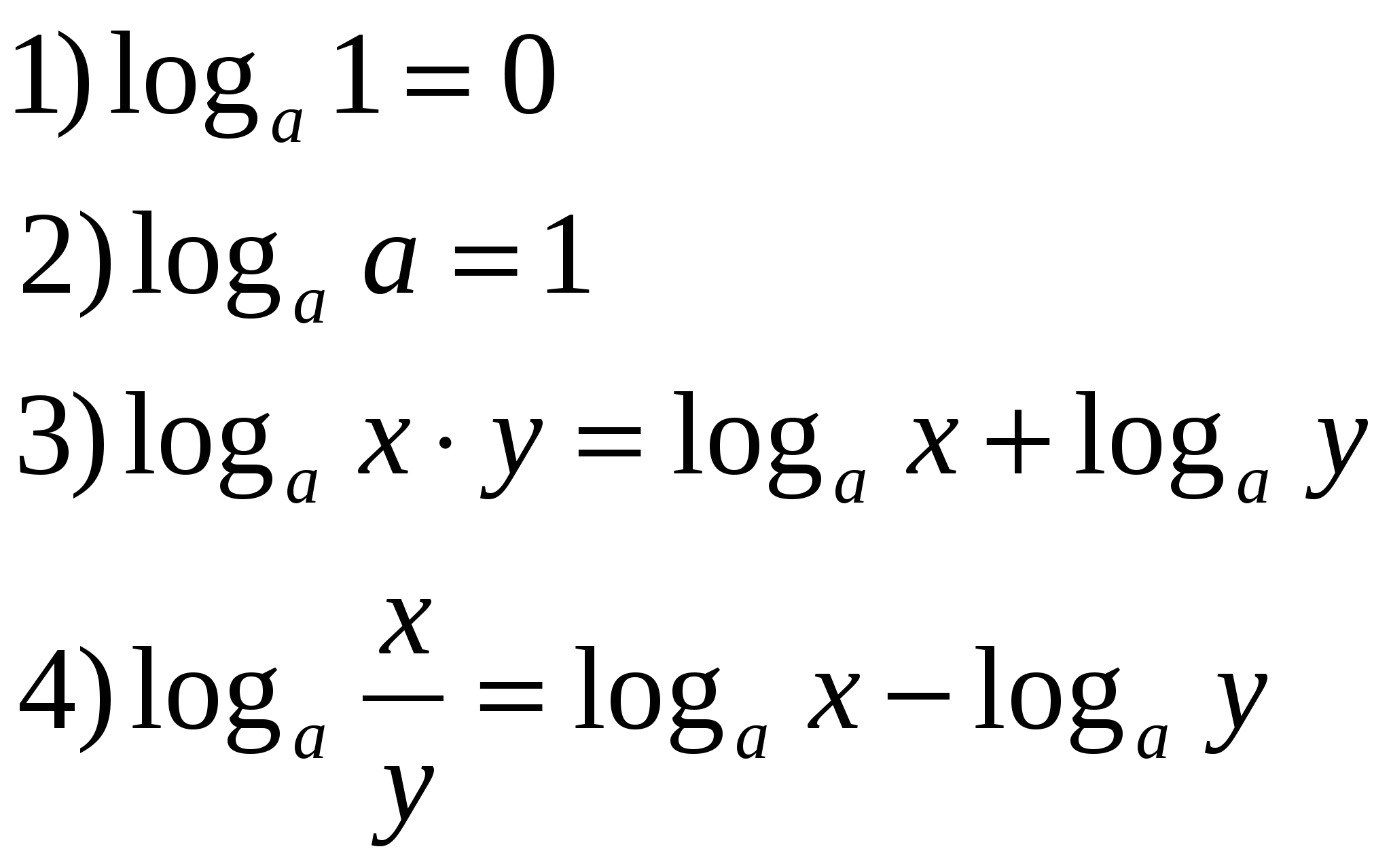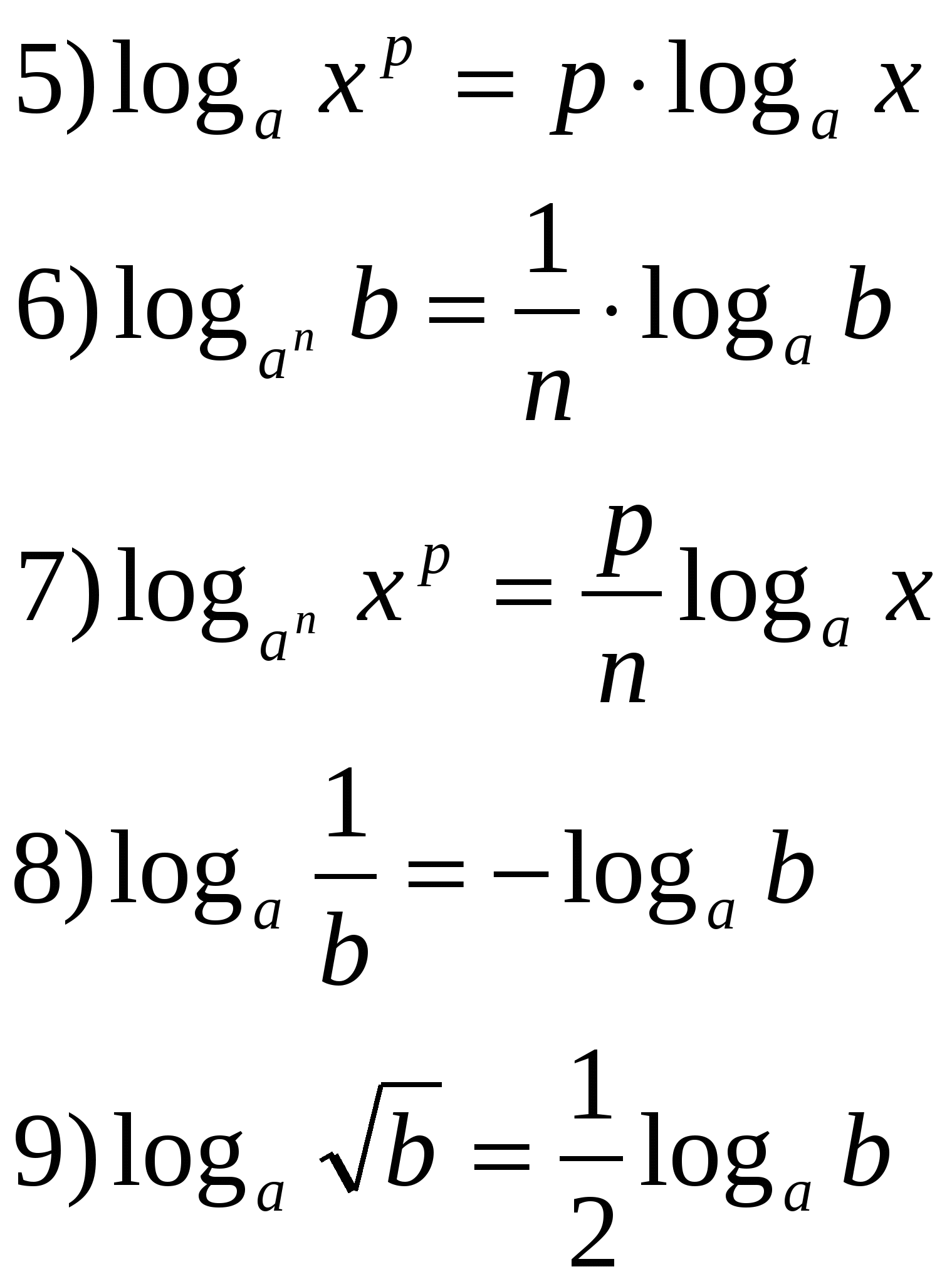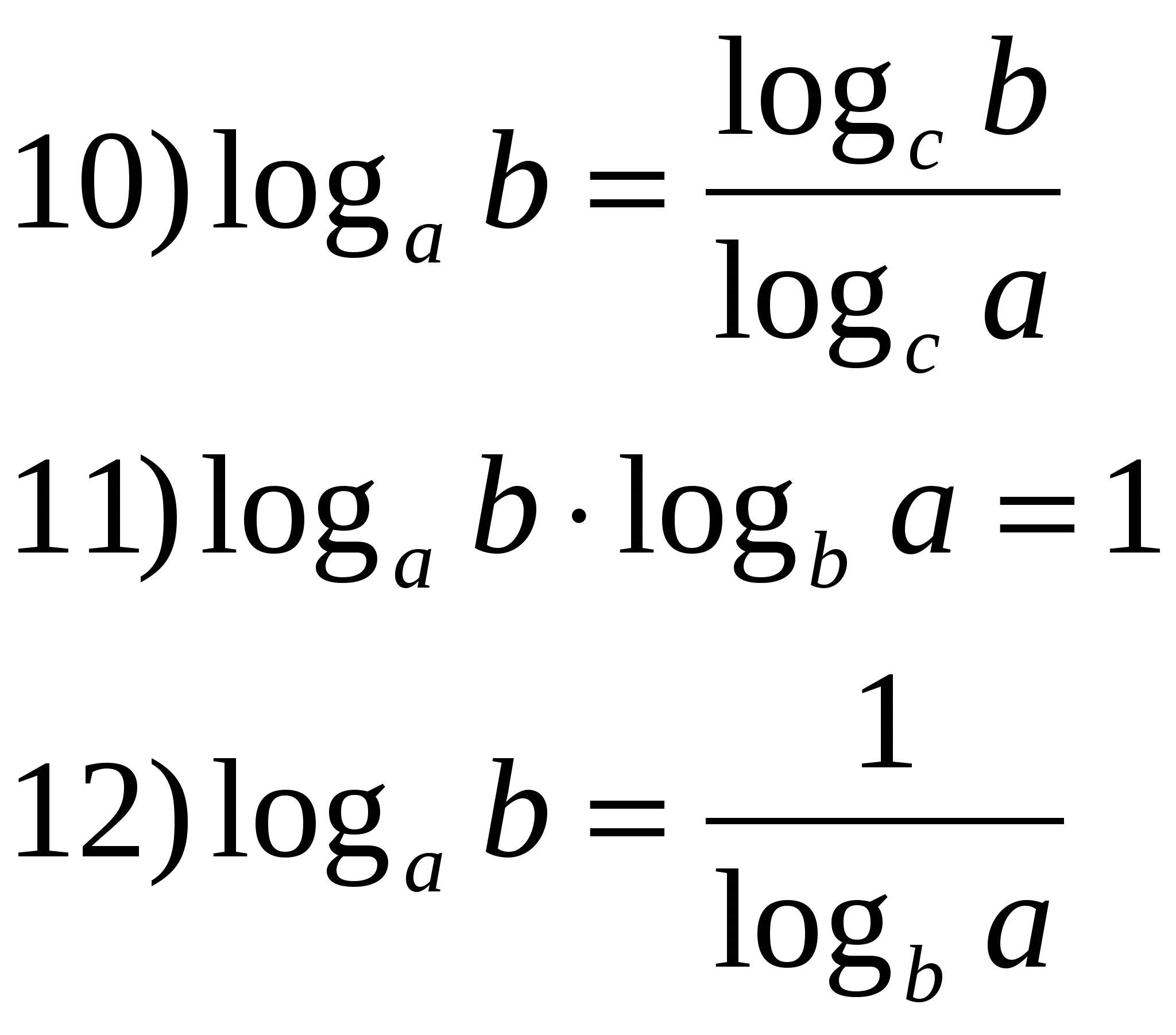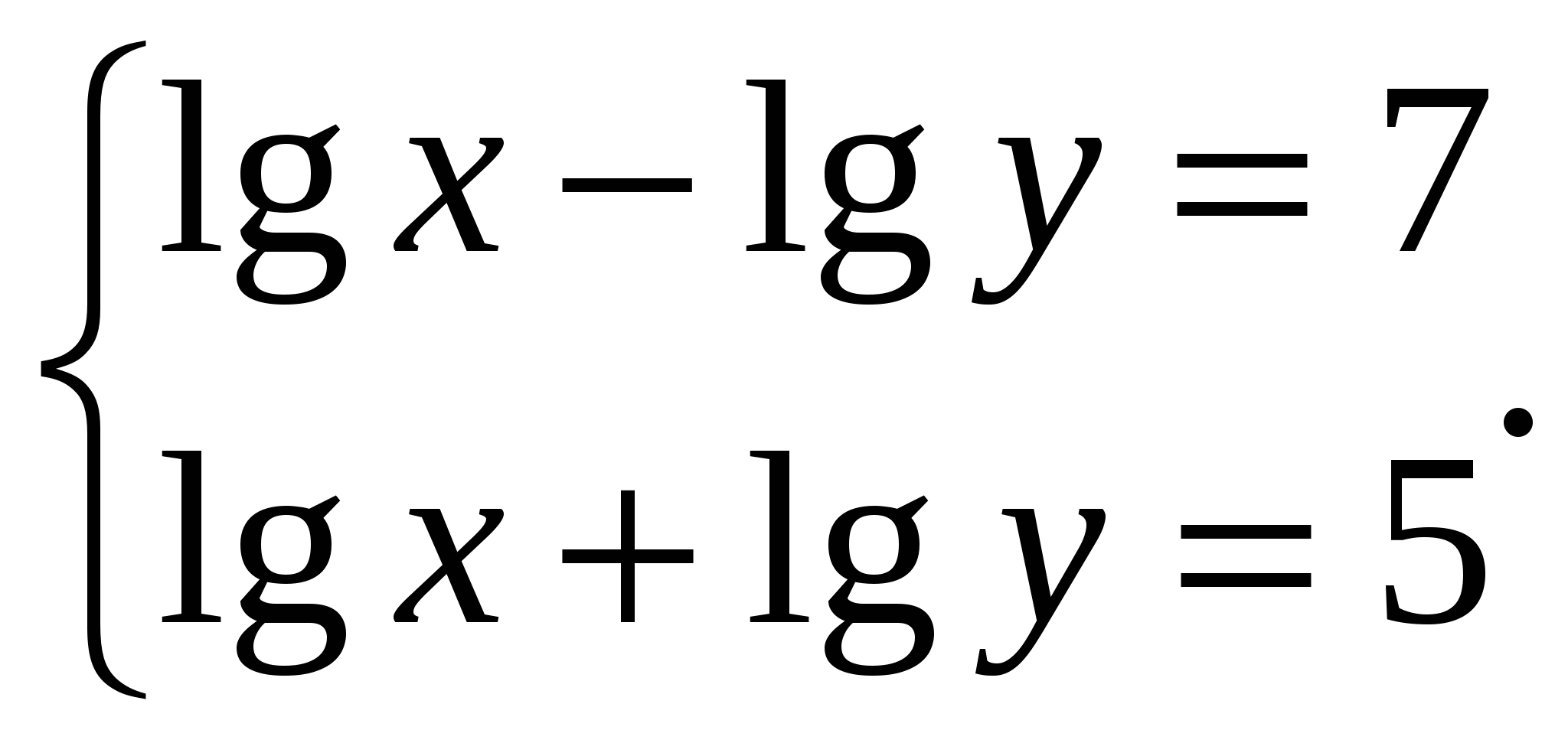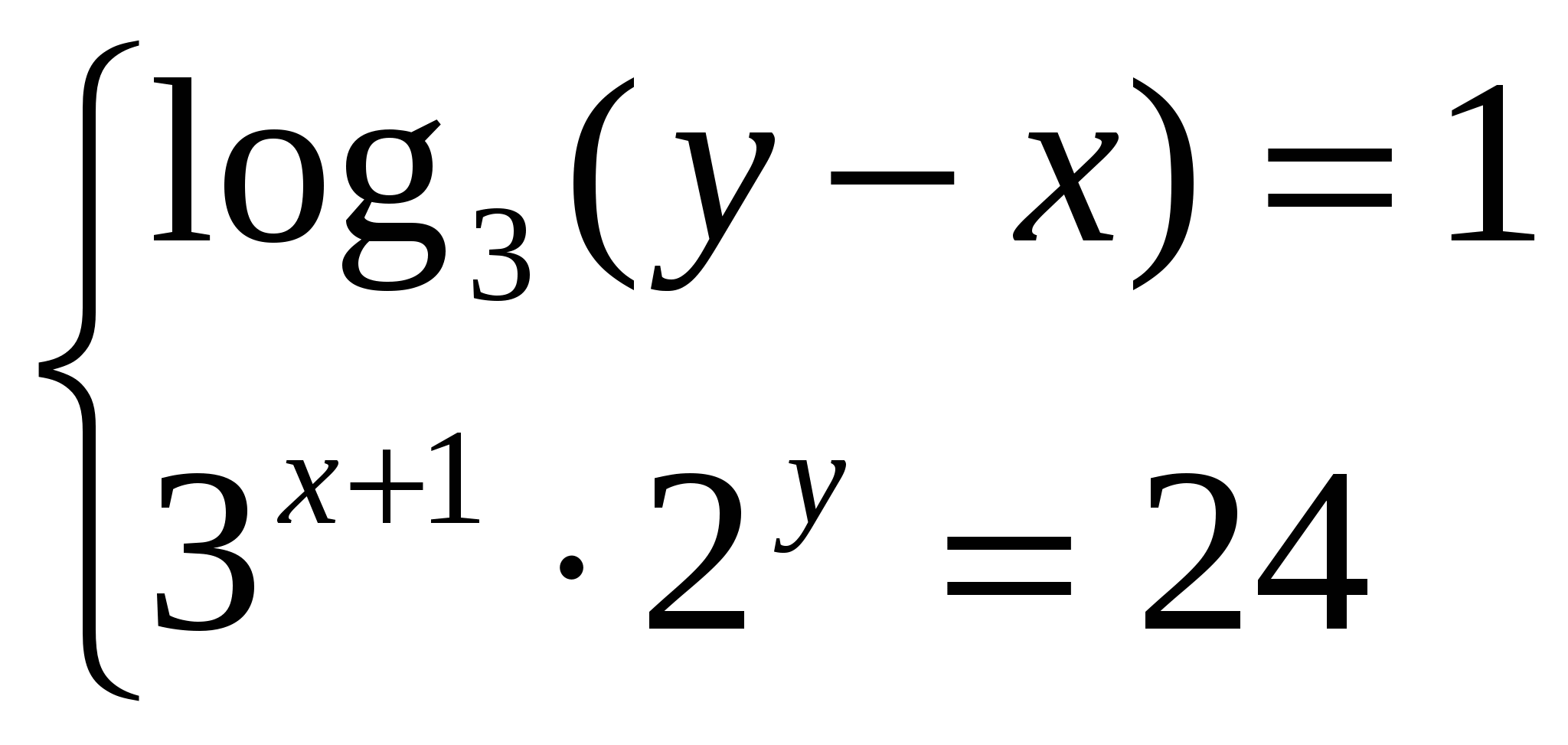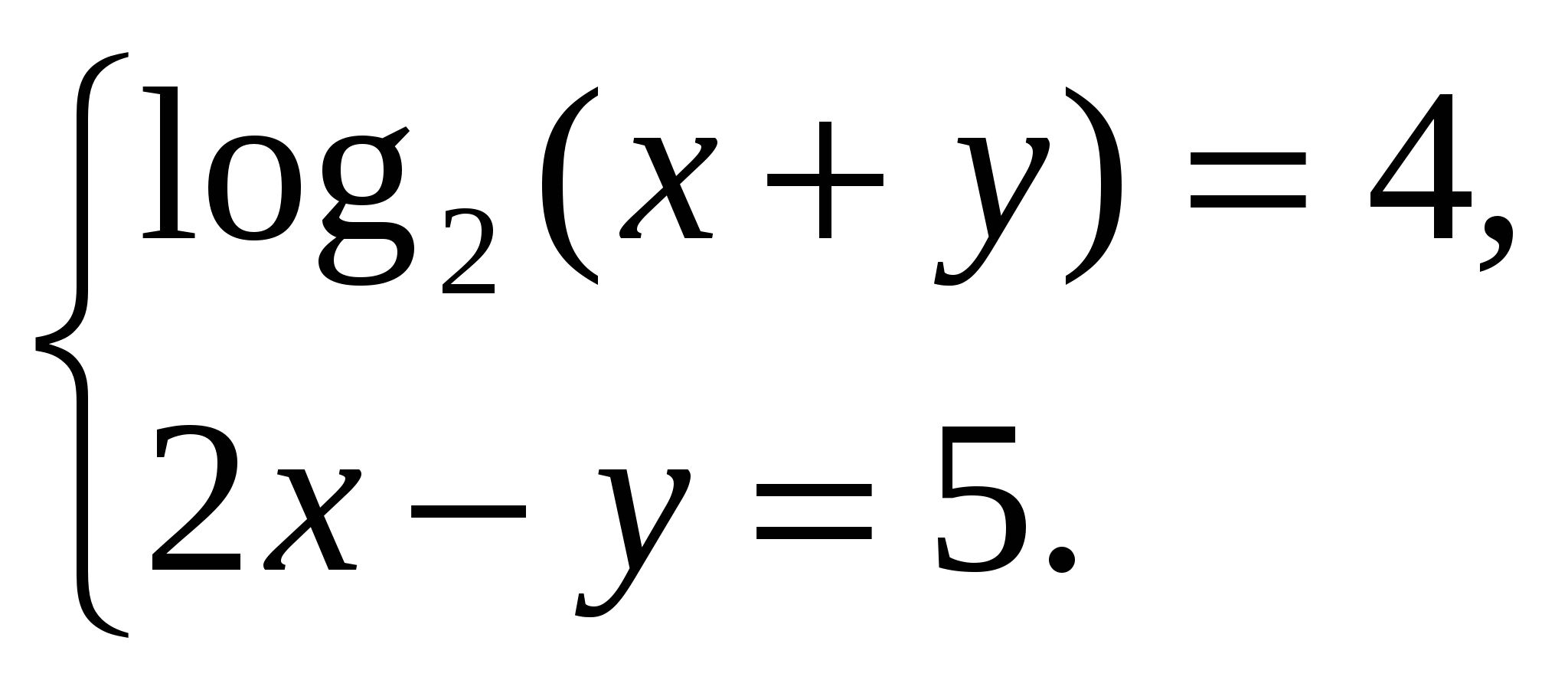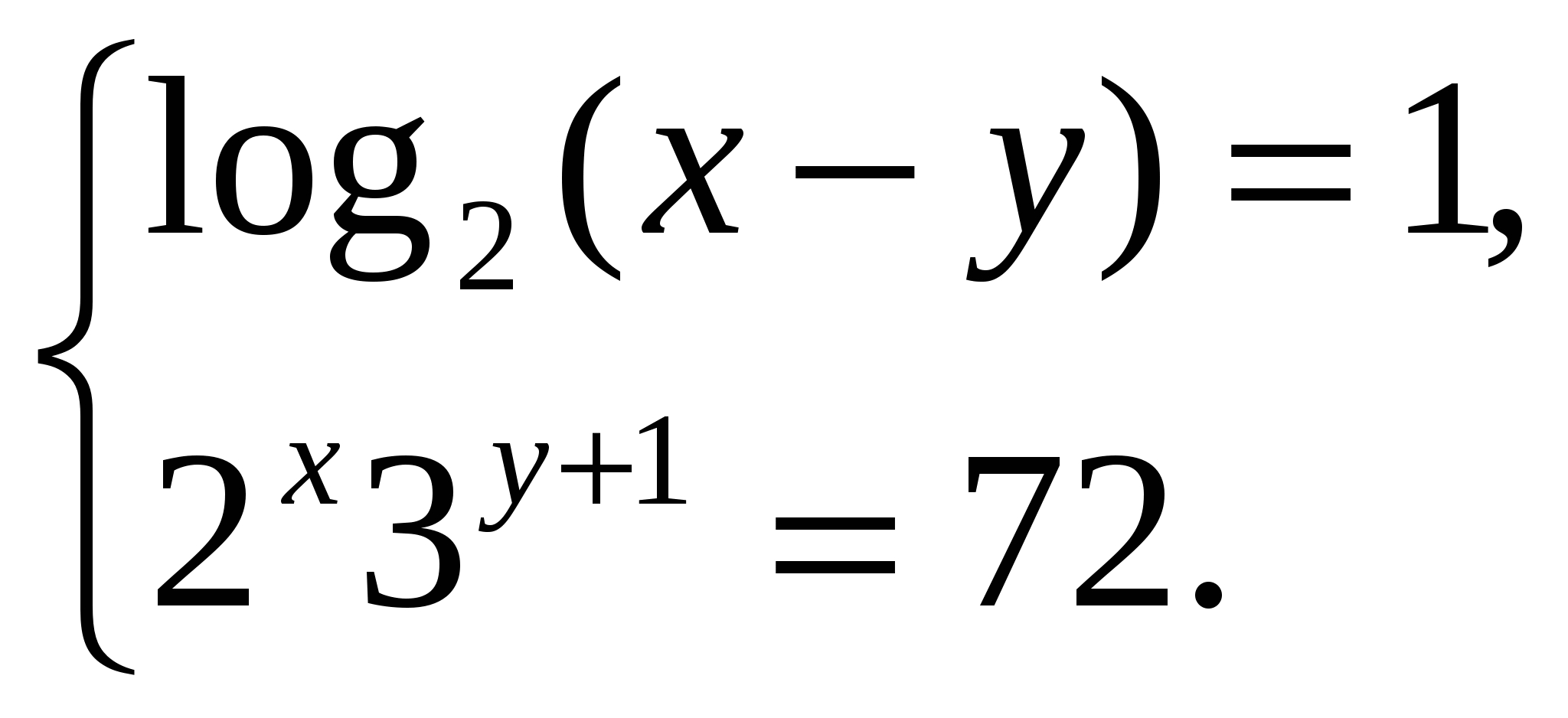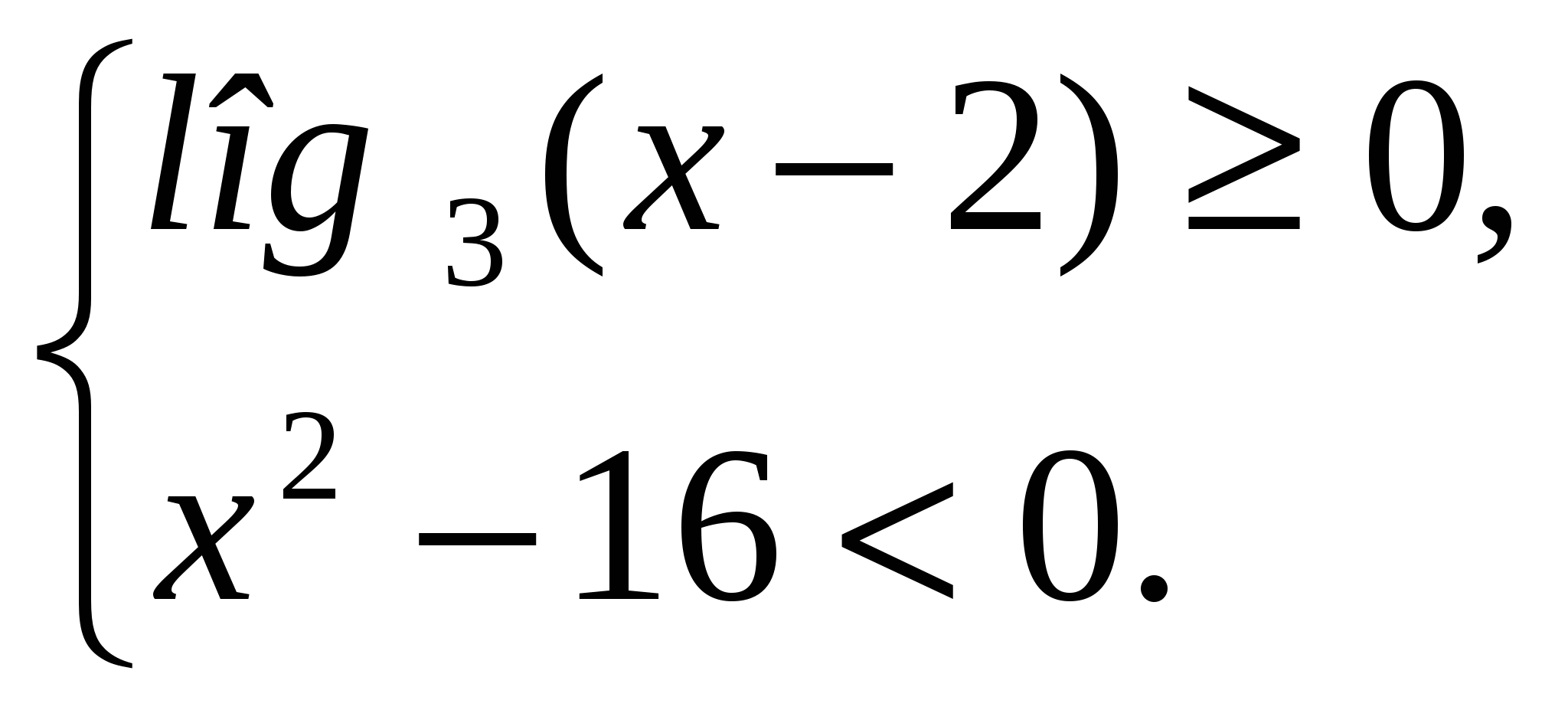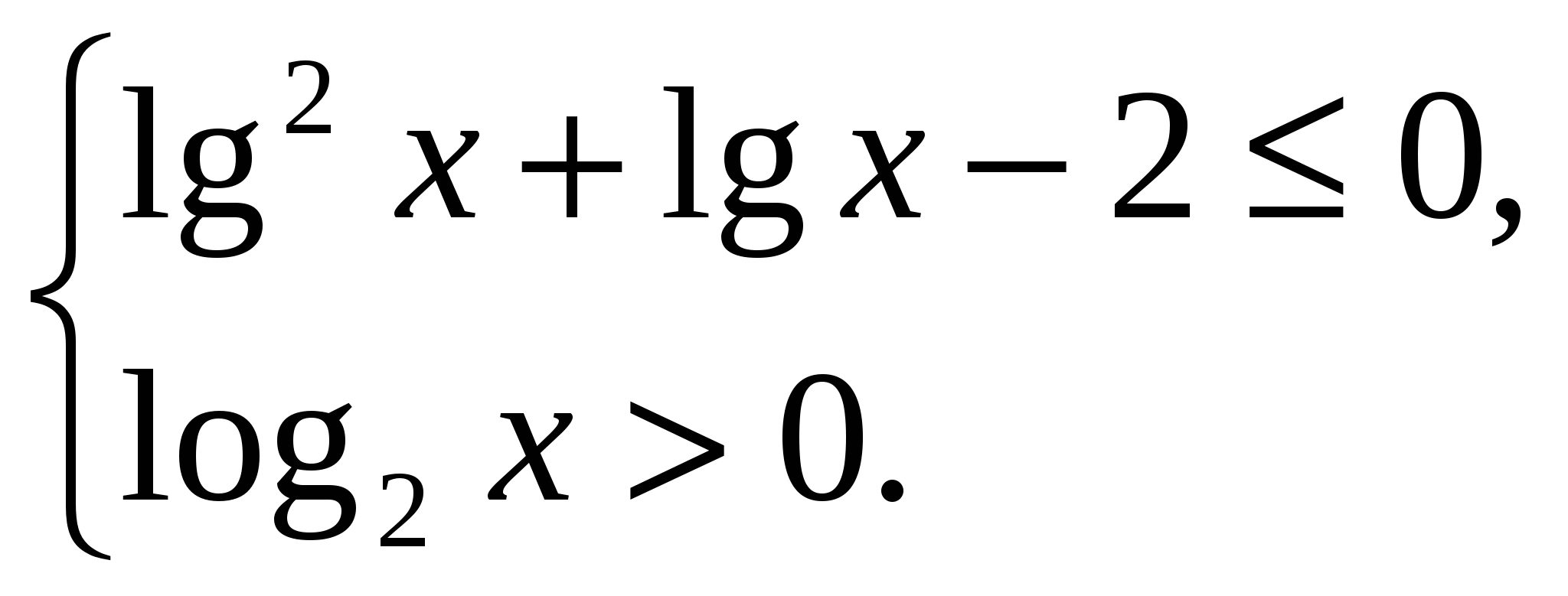Конспект урока «Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов» по математике
Логарифм числа. Основное логарифмическое тождество.
Свойства логарифмов
Справочные сведения
Логарифмом положительного числа b по основанию а ( записывают loga b), где а > 0, a ![]() 1, называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
1, называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
Равенство ![]() , где а > 0, a
, где а > 0, a ![]() 1, b > 0, называют основным логарифмическим тождеством.
1, b > 0, называют основным логарифмическим тождеством.
x = logab – корень уравнения ax = b, где а > 0, a ![]() 1, b > 0.
1, b > 0.
Логарифм числа по основанию 10 называется десятичным логарифмом: log10 b = lg b.
Логарифм числа по основанию е называется натуральным логарифмом: logе b = ln b.
|
|
|
Примеры с решениями
-
Вычислить: 1)
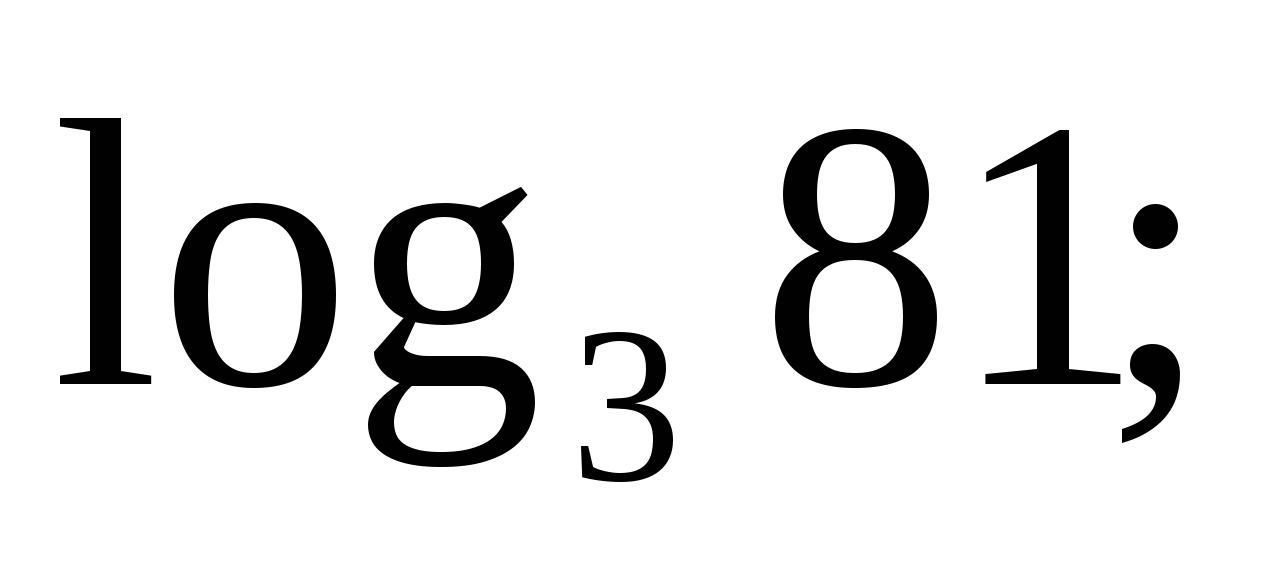 2)
2) 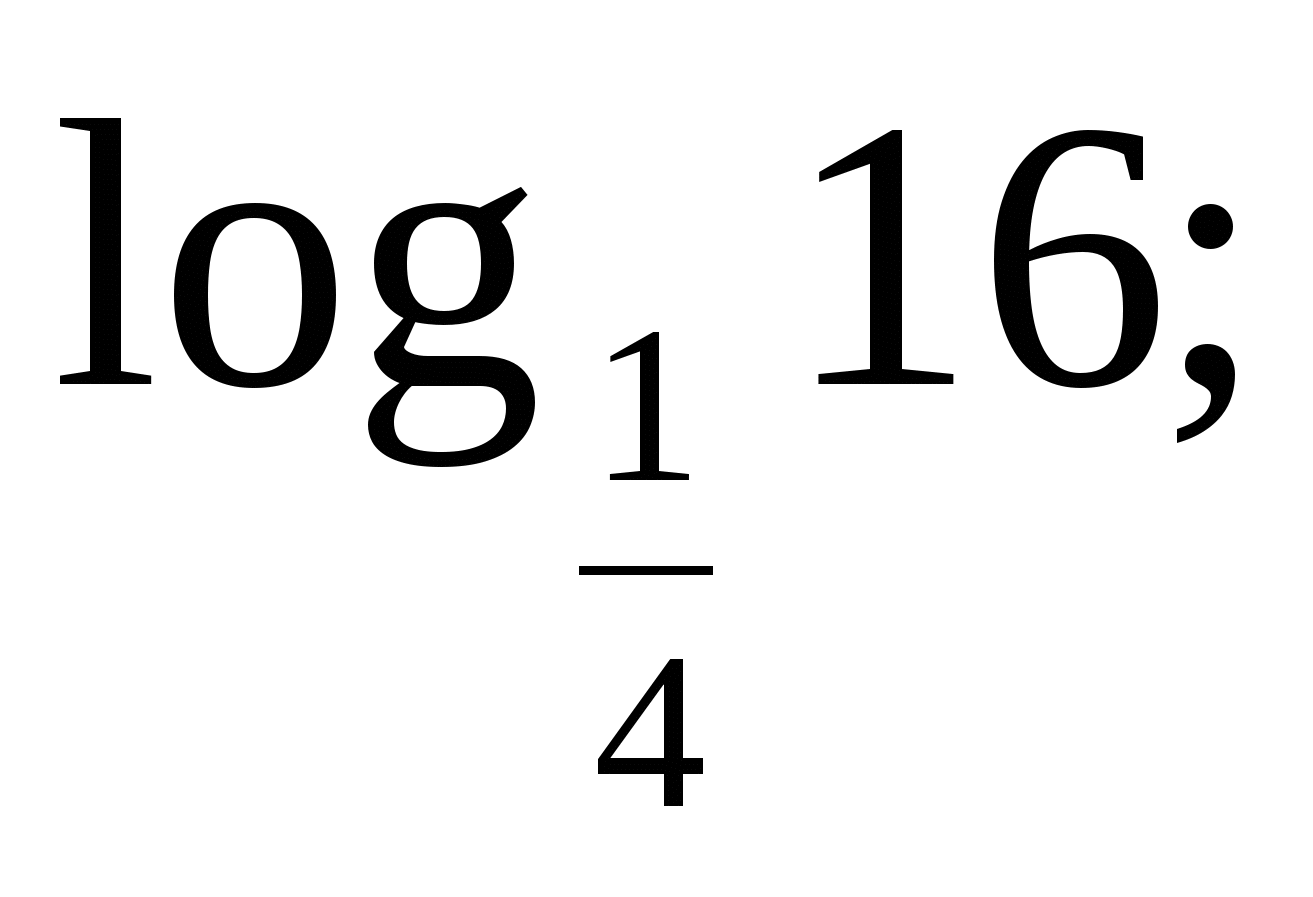 3)
3) 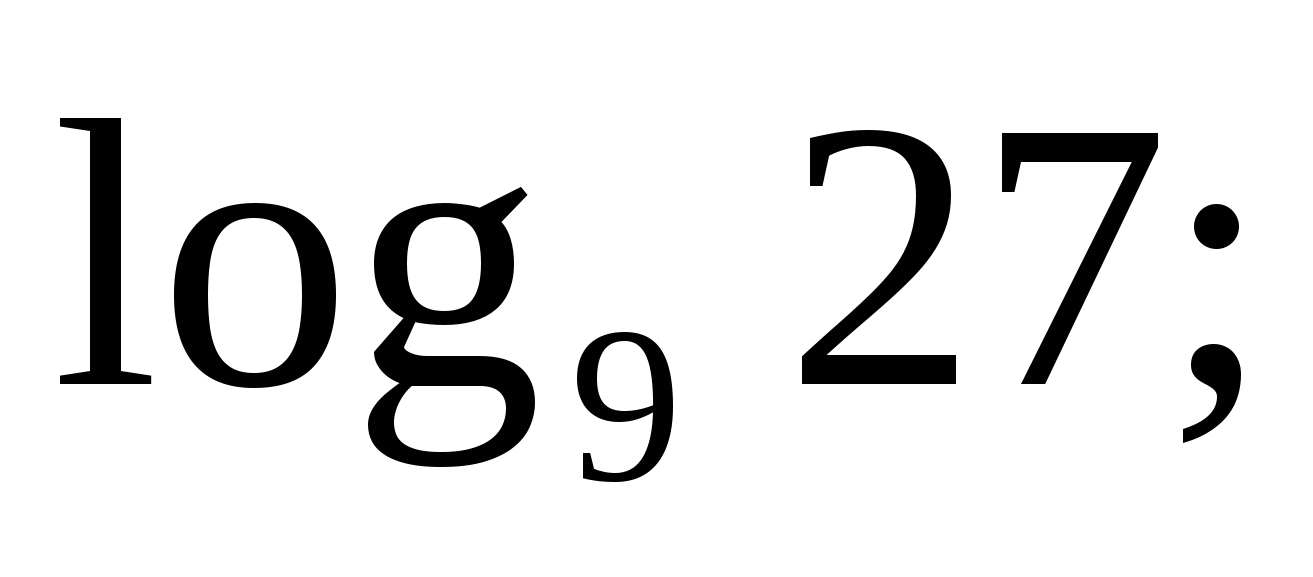
Решение. 1) ![]() , так как 34 = 81.
, так как 34 = 81.
2) Пусть ![]() . Тогда по определению логарифма
. Тогда по определению логарифма ![]() , или
, или ![]() , откуда
, откуда ![]() ,
,![]() .
.
3) Пусть ![]() . Тогда по определению логарифма
. Тогда по определению логарифма ![]() , откуда
, откуда ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
-
Найти: 1)
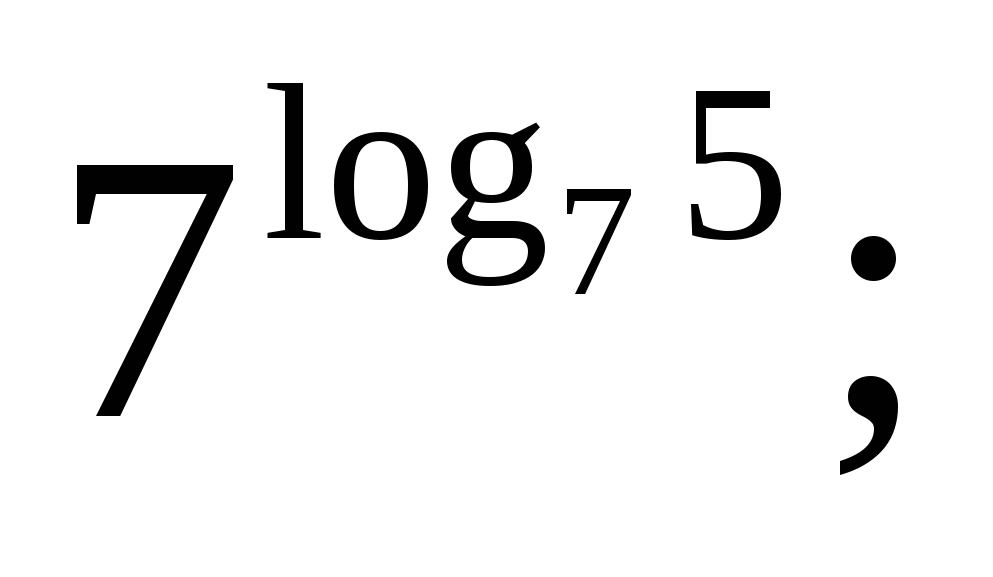 2)
2) 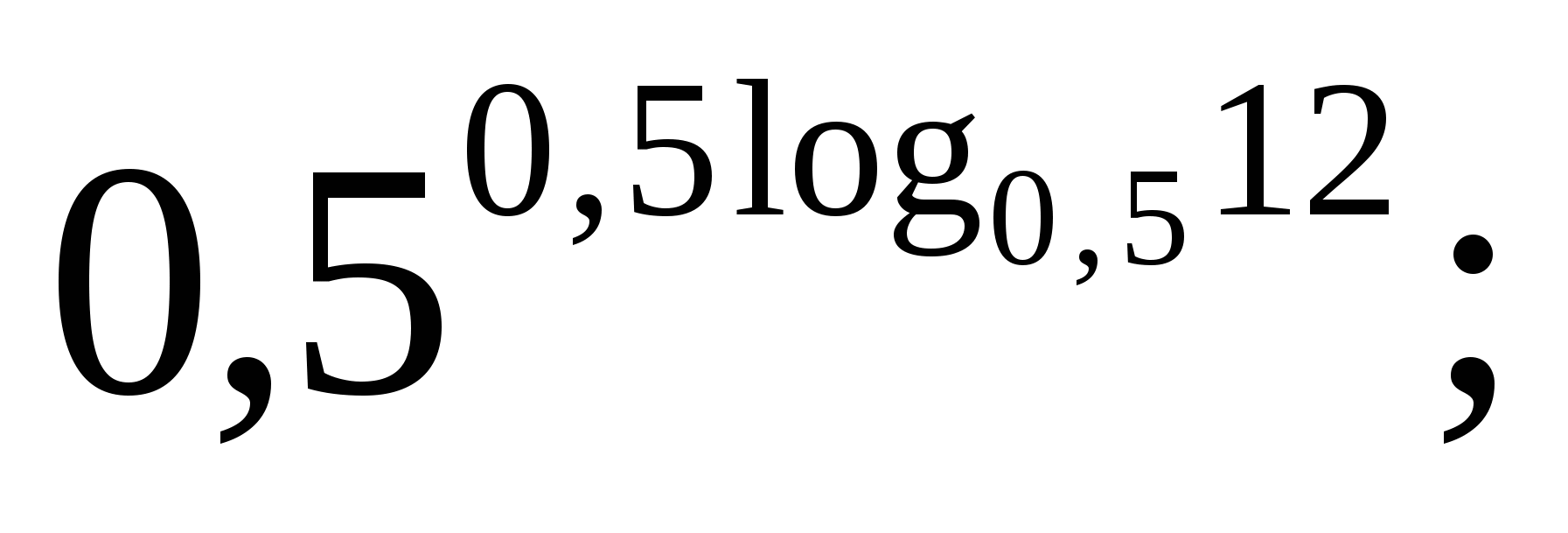 3)
3) 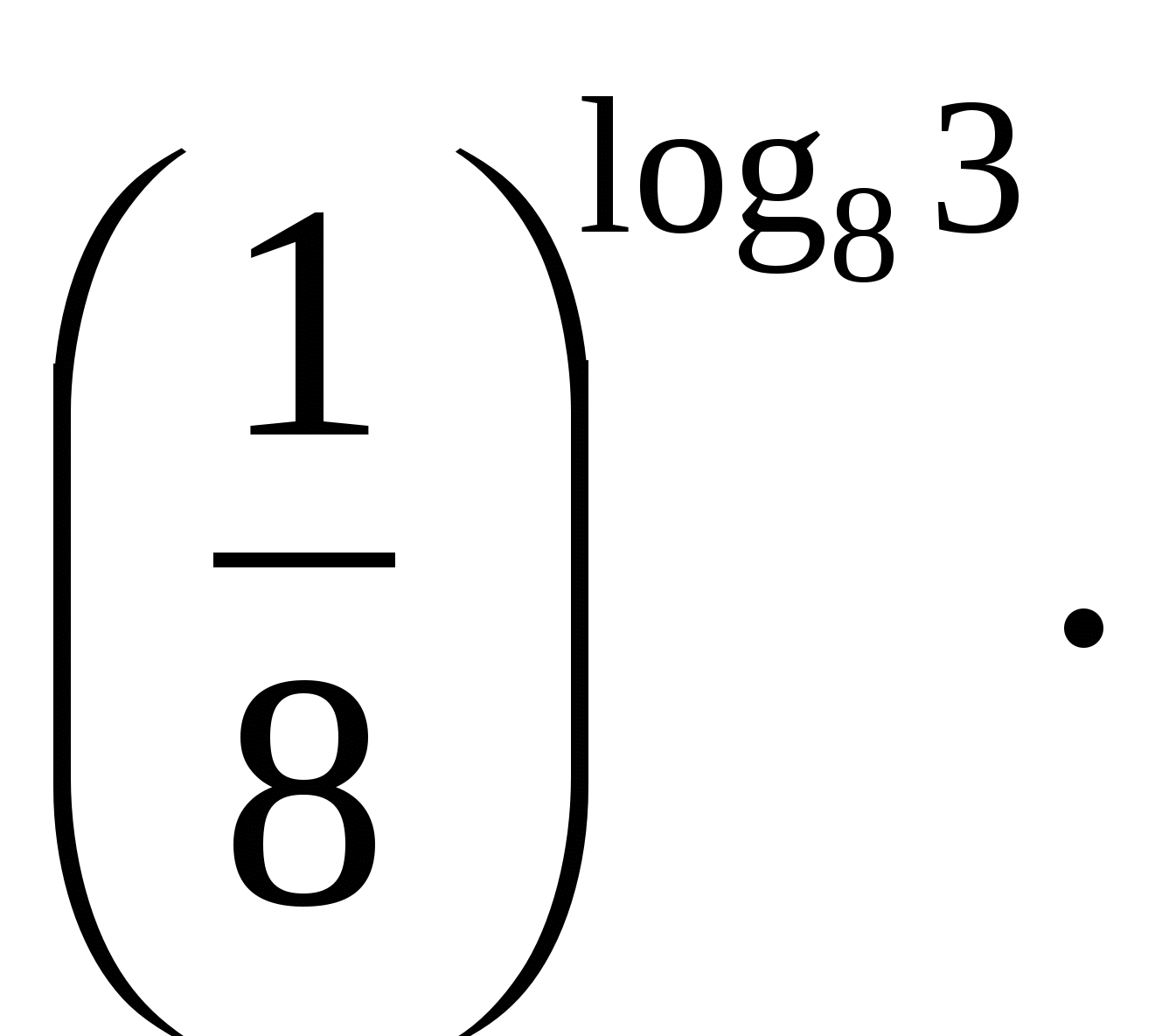
Решение. 1) По определению логарифма (согласно основному логарифмическому тождеству) ![]() 2)
2) ![]()
3) ![]()
3. Вычислить:
1) ![]() 2)
2) ![]() 3)
3) ![]()
Решение.
1) ![]()
2) ![]()
3) 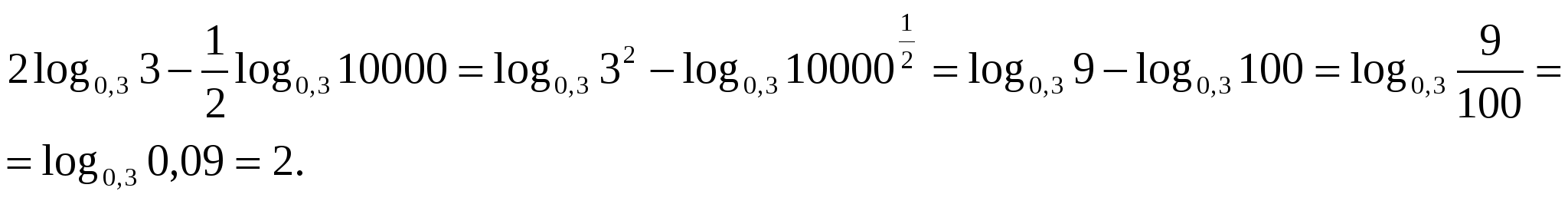
Дидактический материал
-
Вычислить:
-
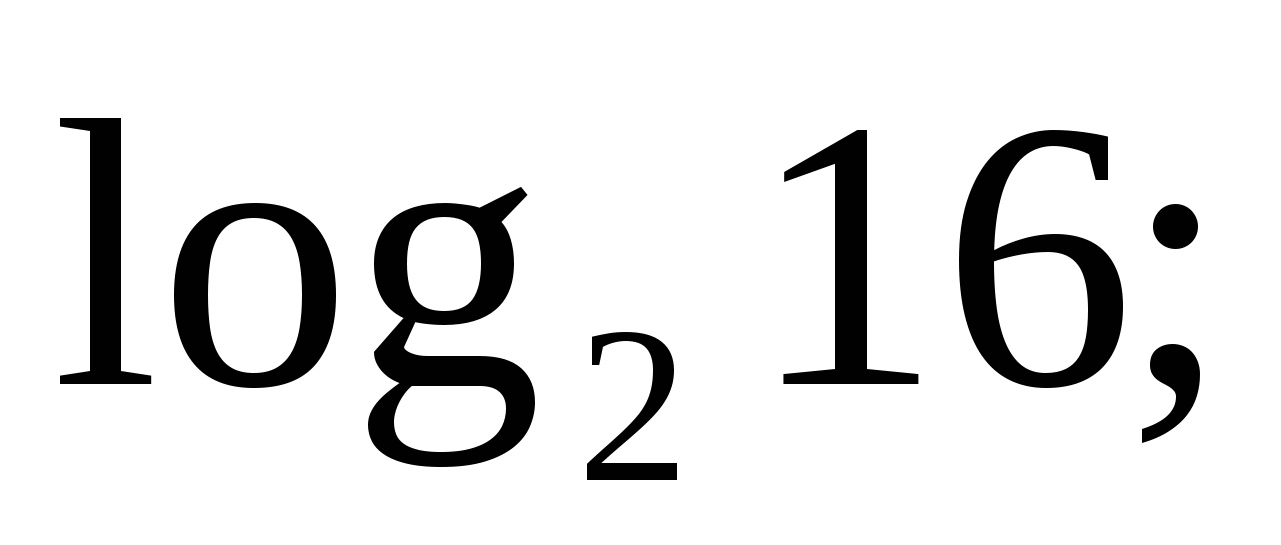 2)
2) 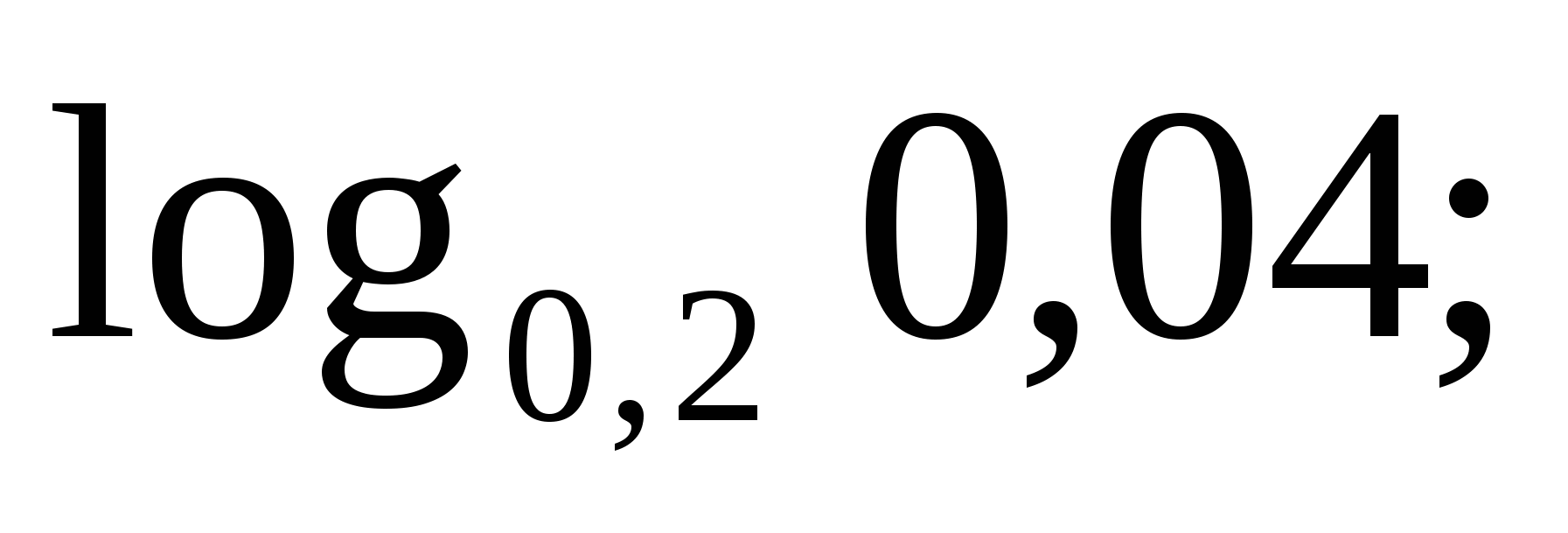 3)
3) 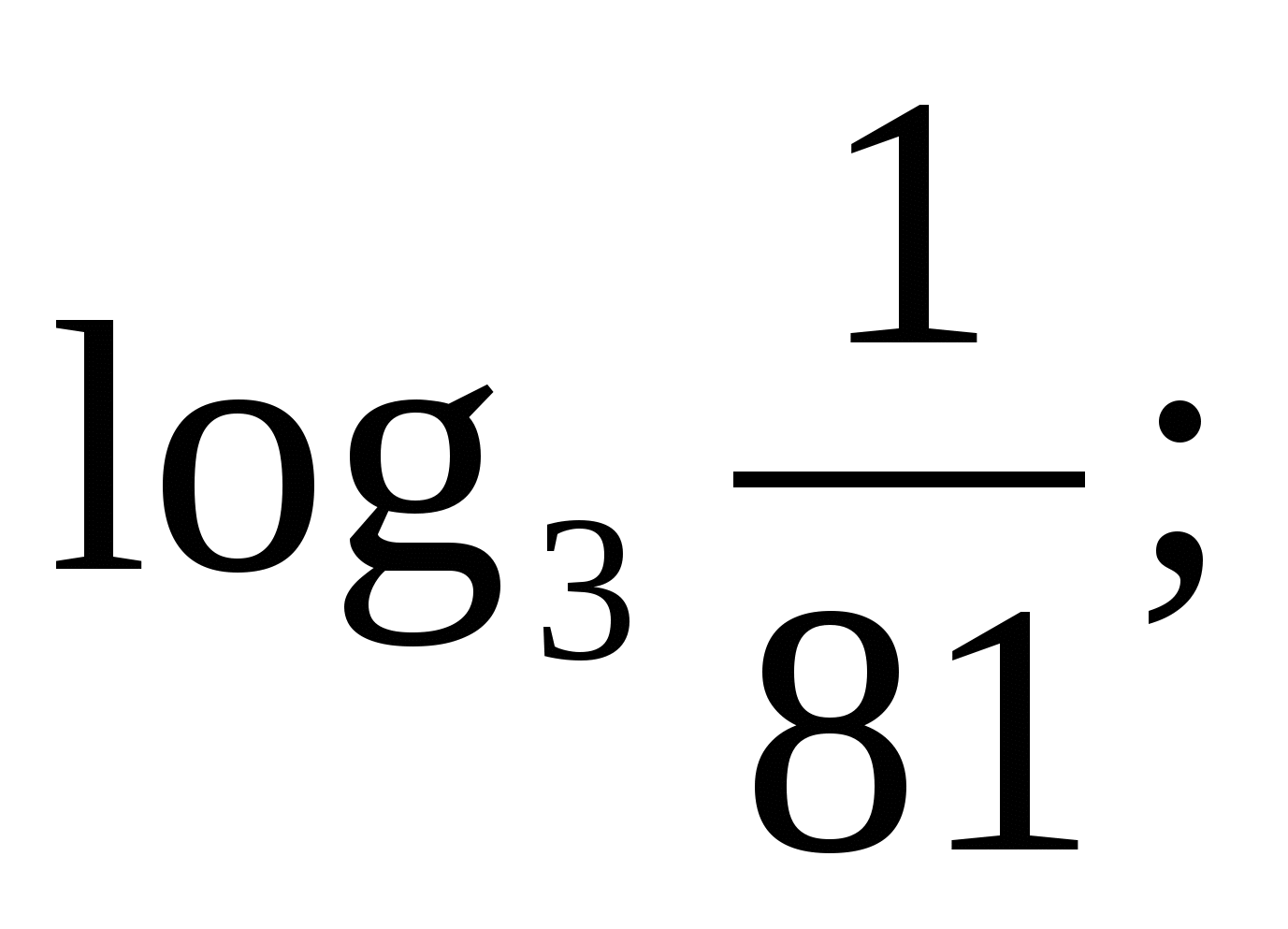
-
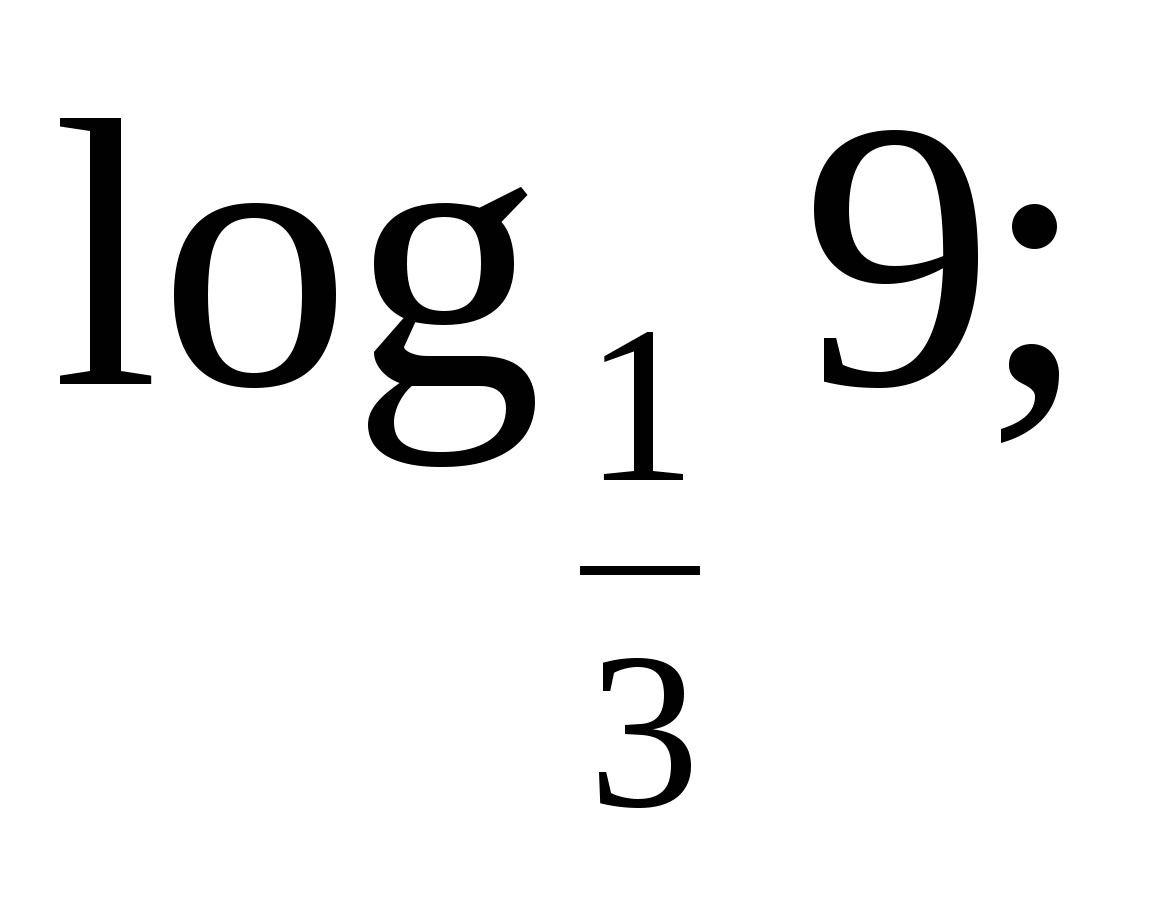 5)
5) 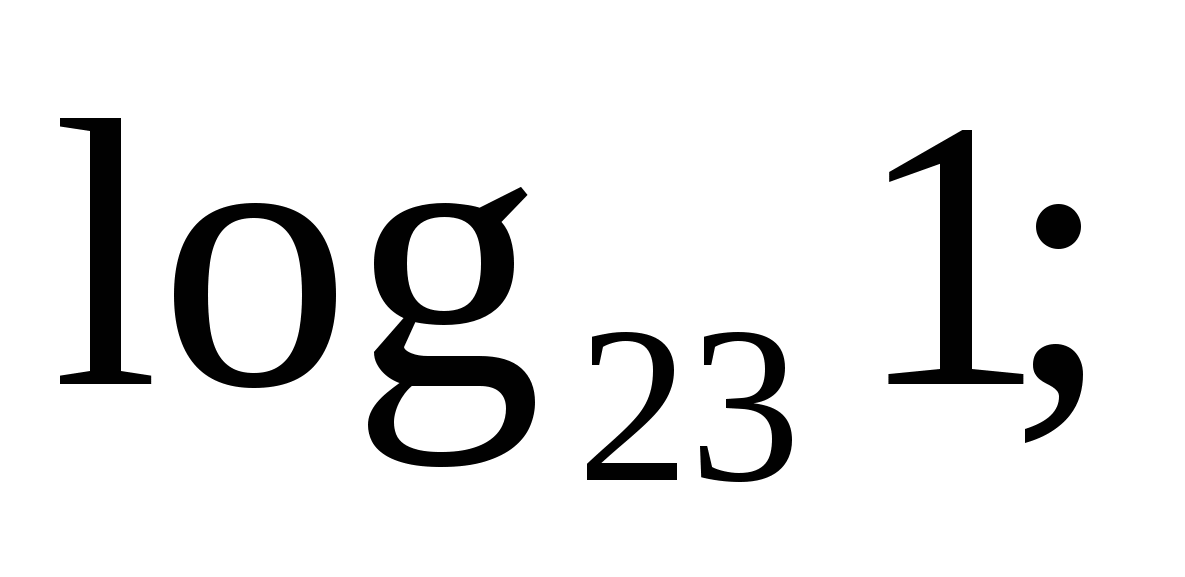 6)
6) 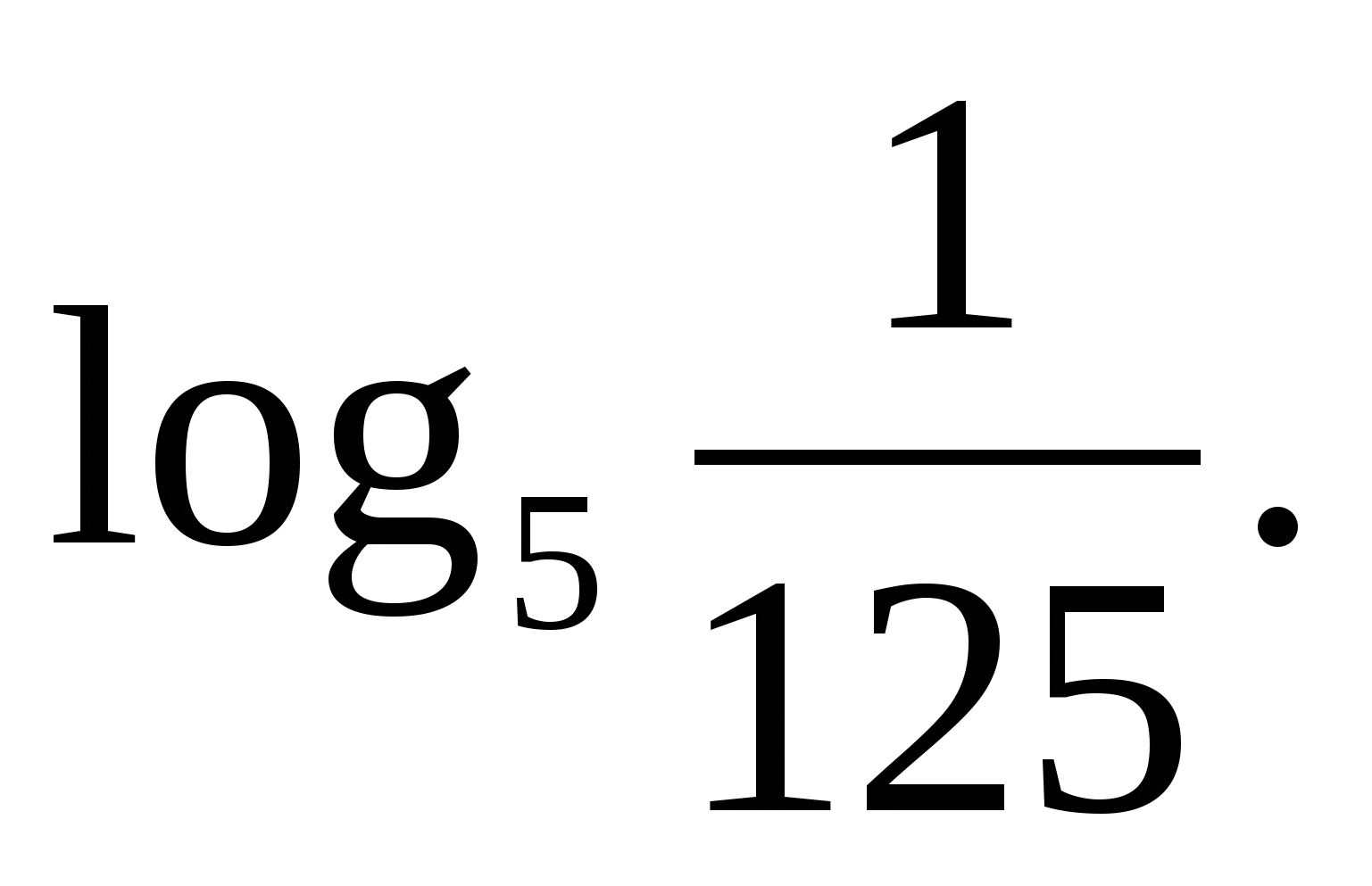
Ответы: - 4; 4; -3; - 2; 2; 0.
-
Вычислите десятичные логарифмы:
-
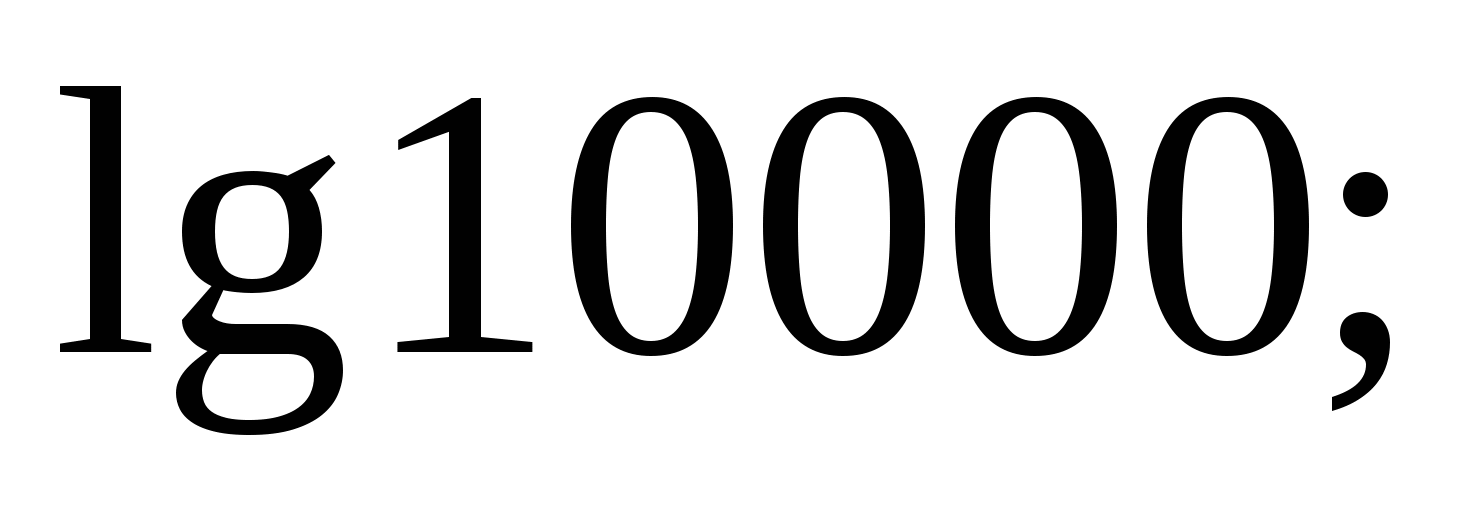 2)
2) 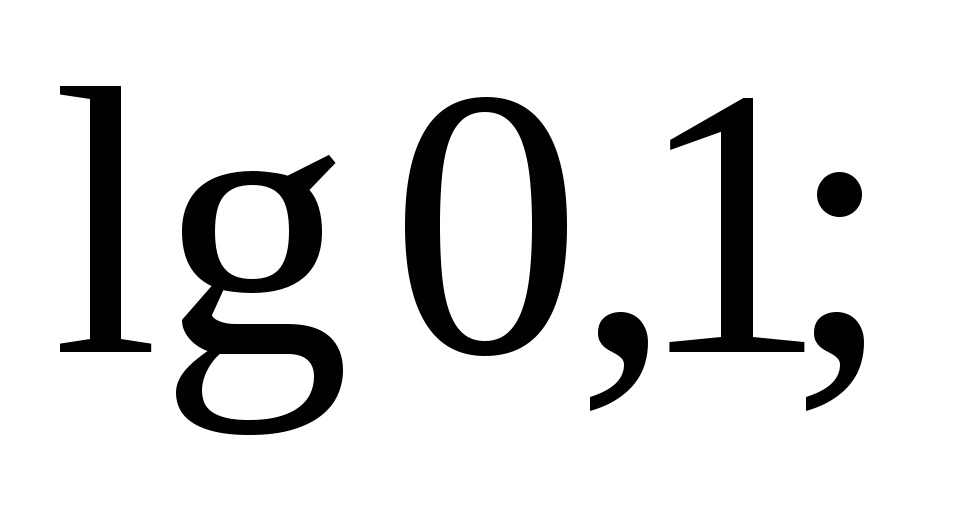 3)
3) 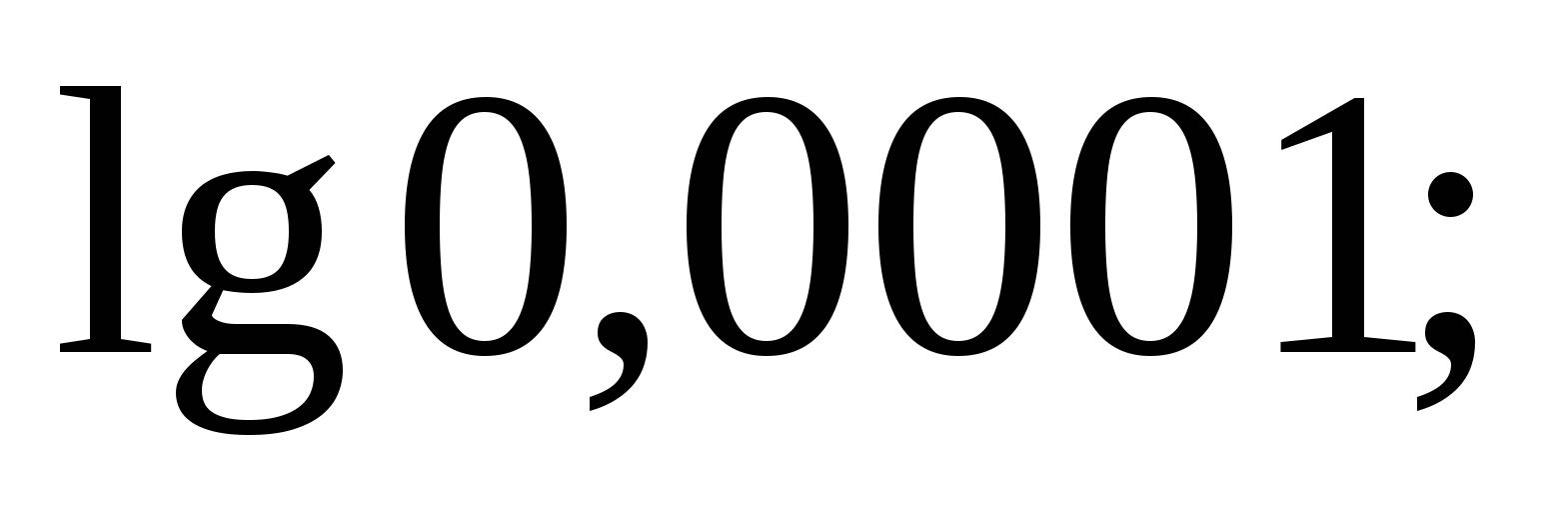 4)
4) 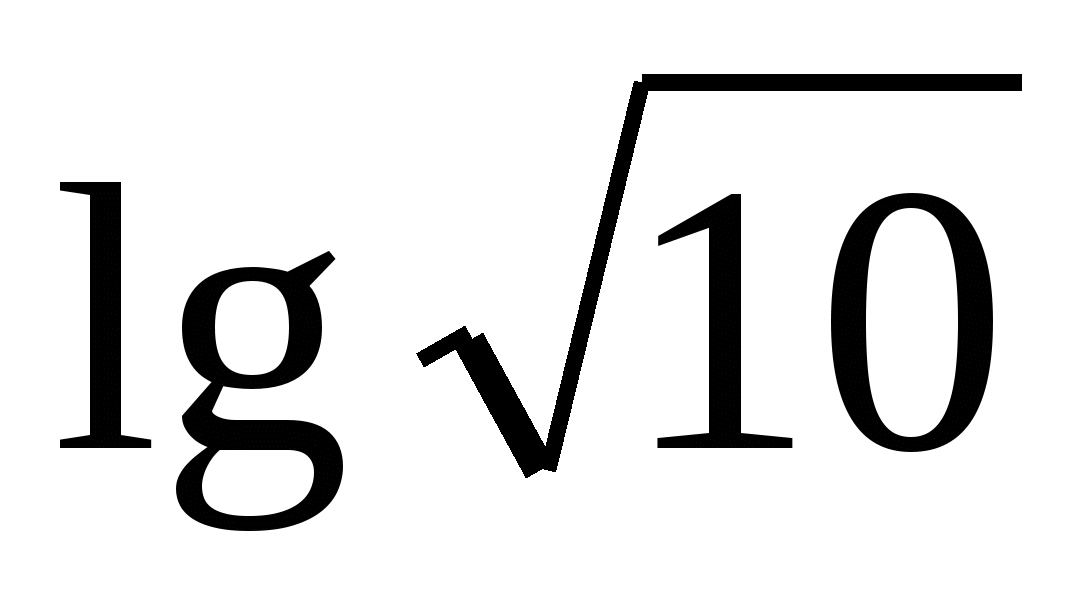 .
.
Ответы: - 4; - 1; ½; 4.
-
Вычислите натуральные логарифмы:
-
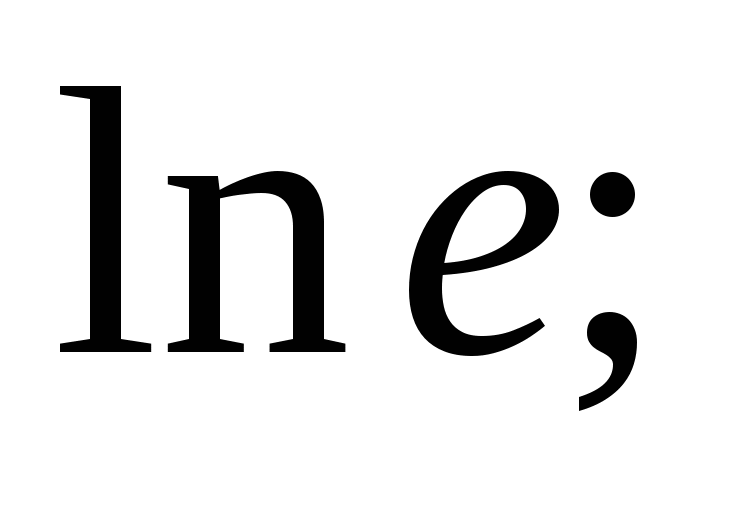 2)
2) 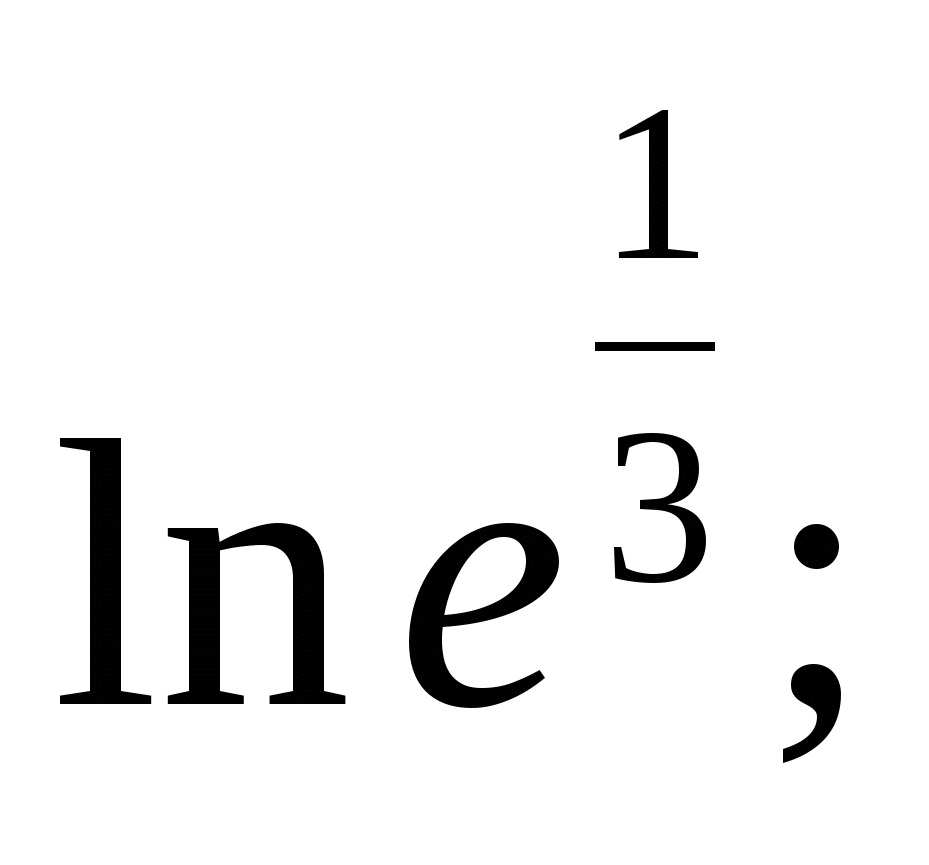 3)
3) 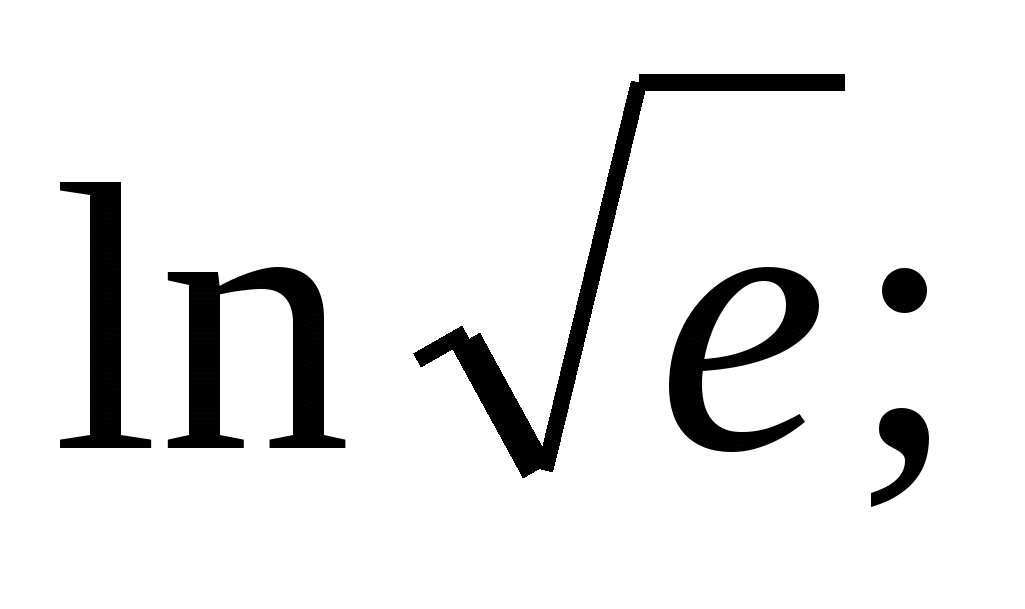 4)
4) 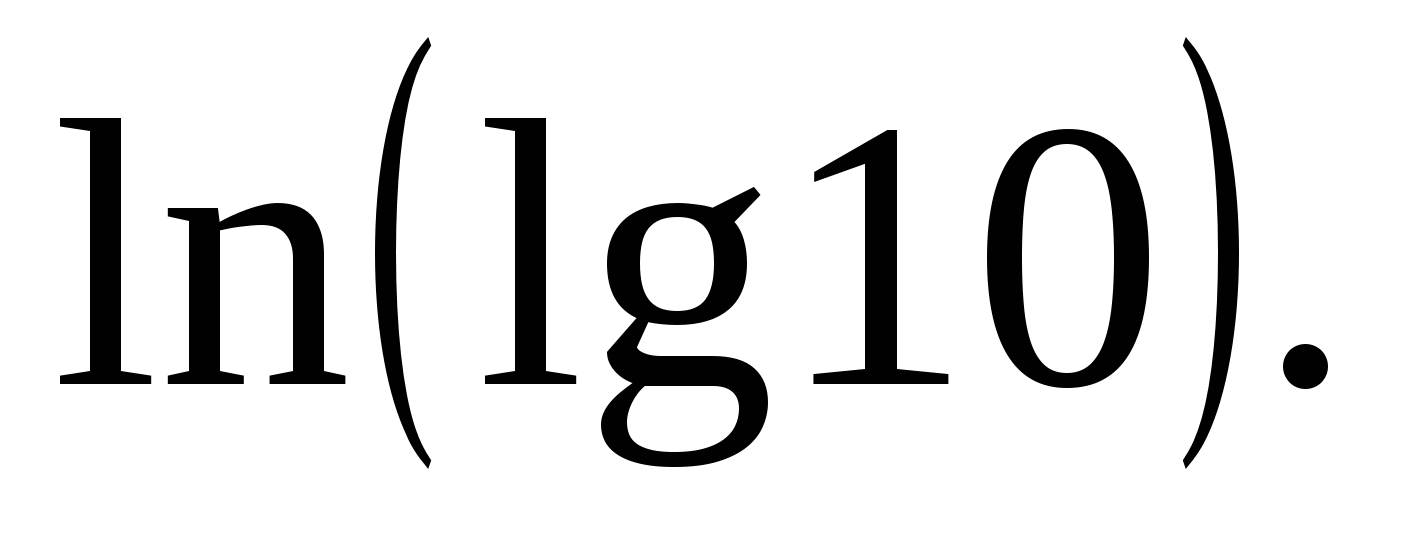
Ответы: ![]()
-
Вычислите:
-
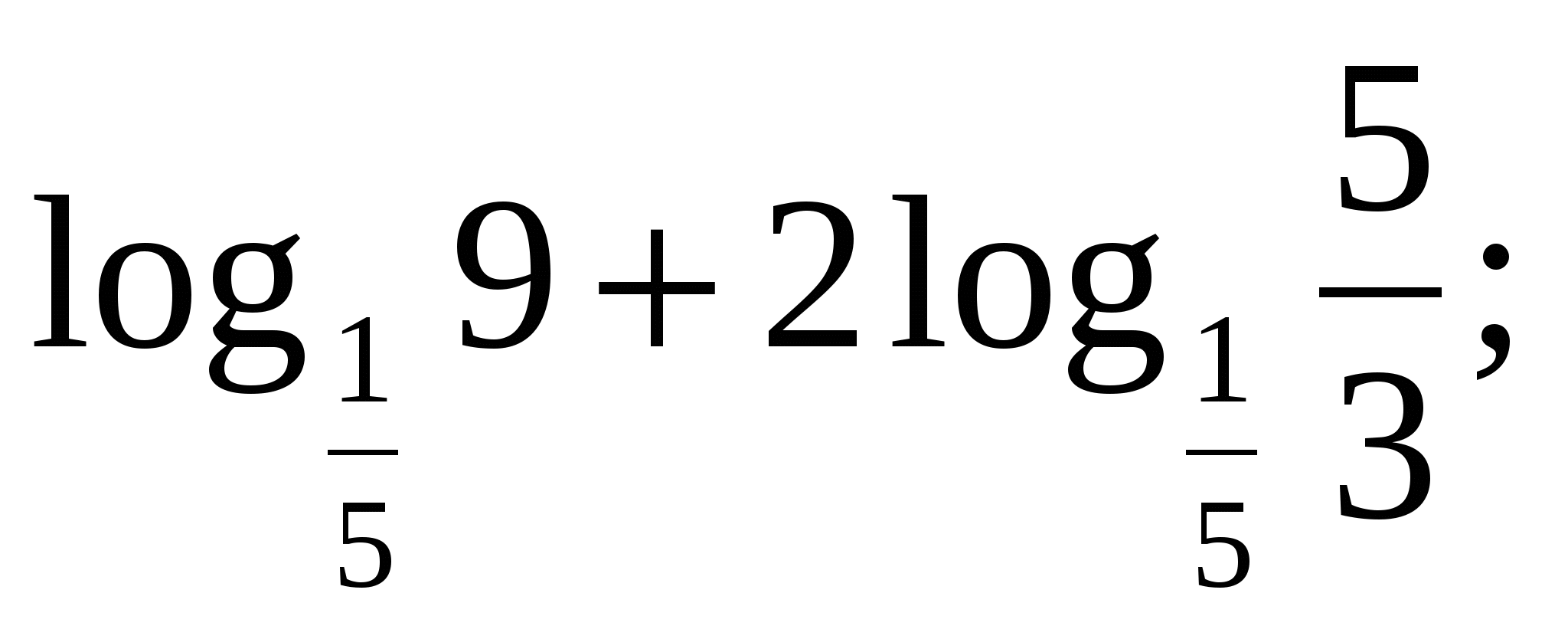 2)
2) 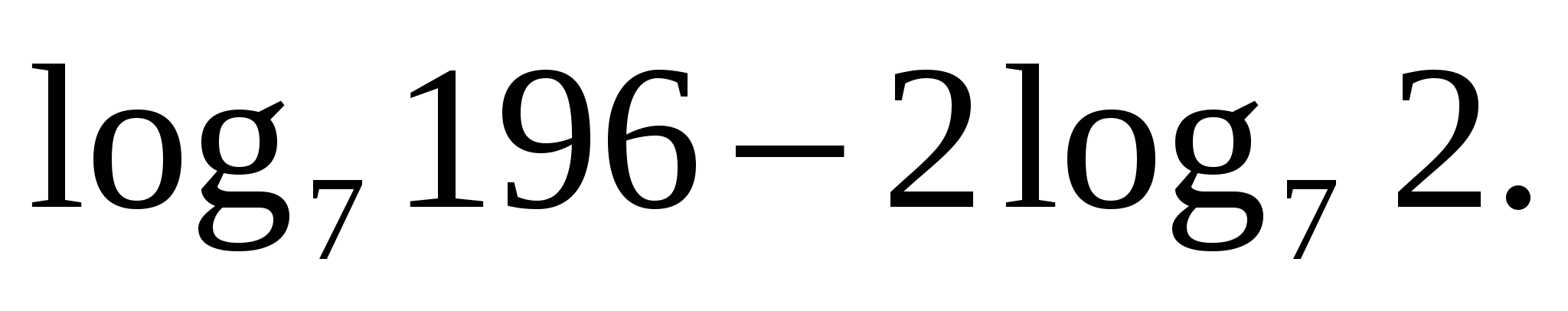
Ответы: - 2; 2.
-
Найдите значения выражений:
-
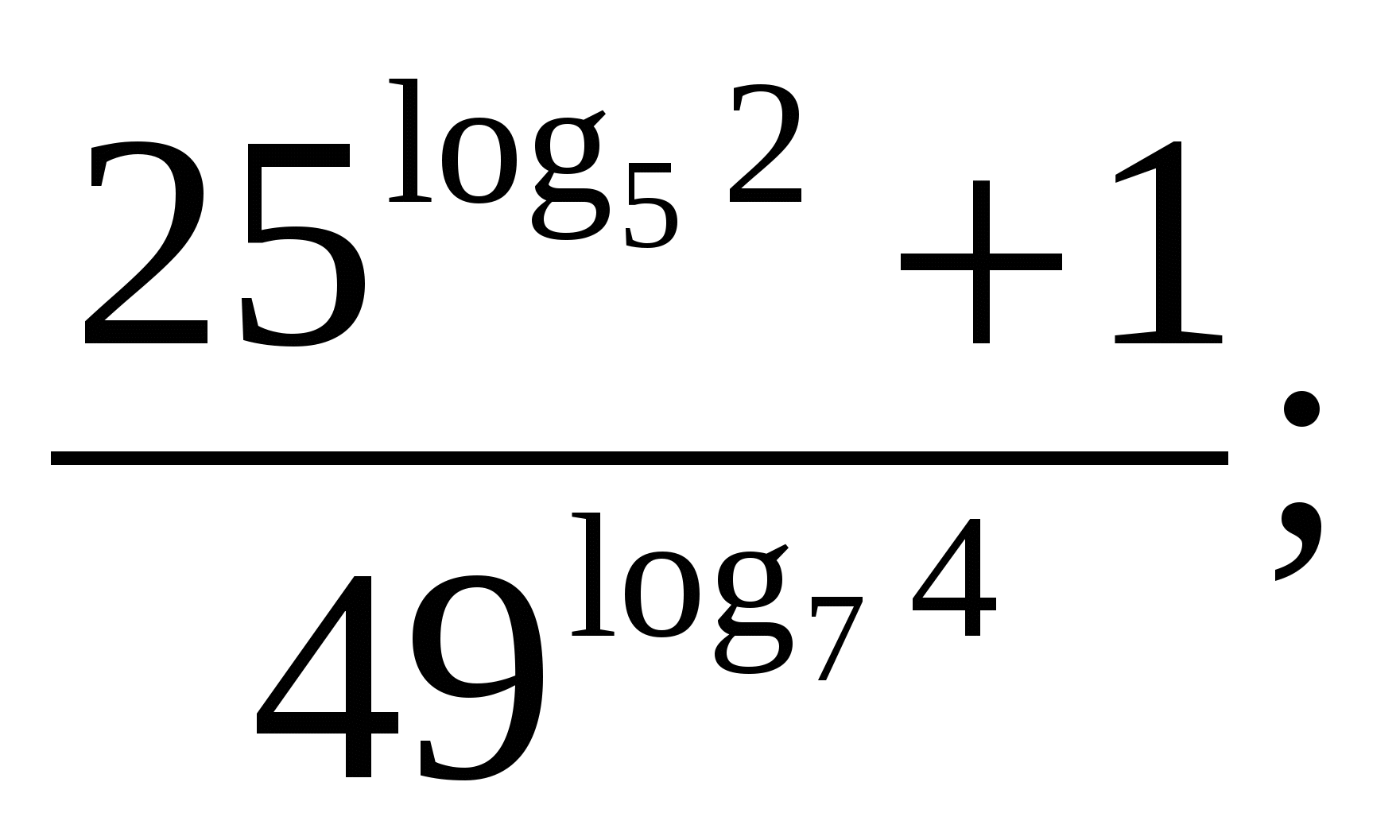 2)
2) 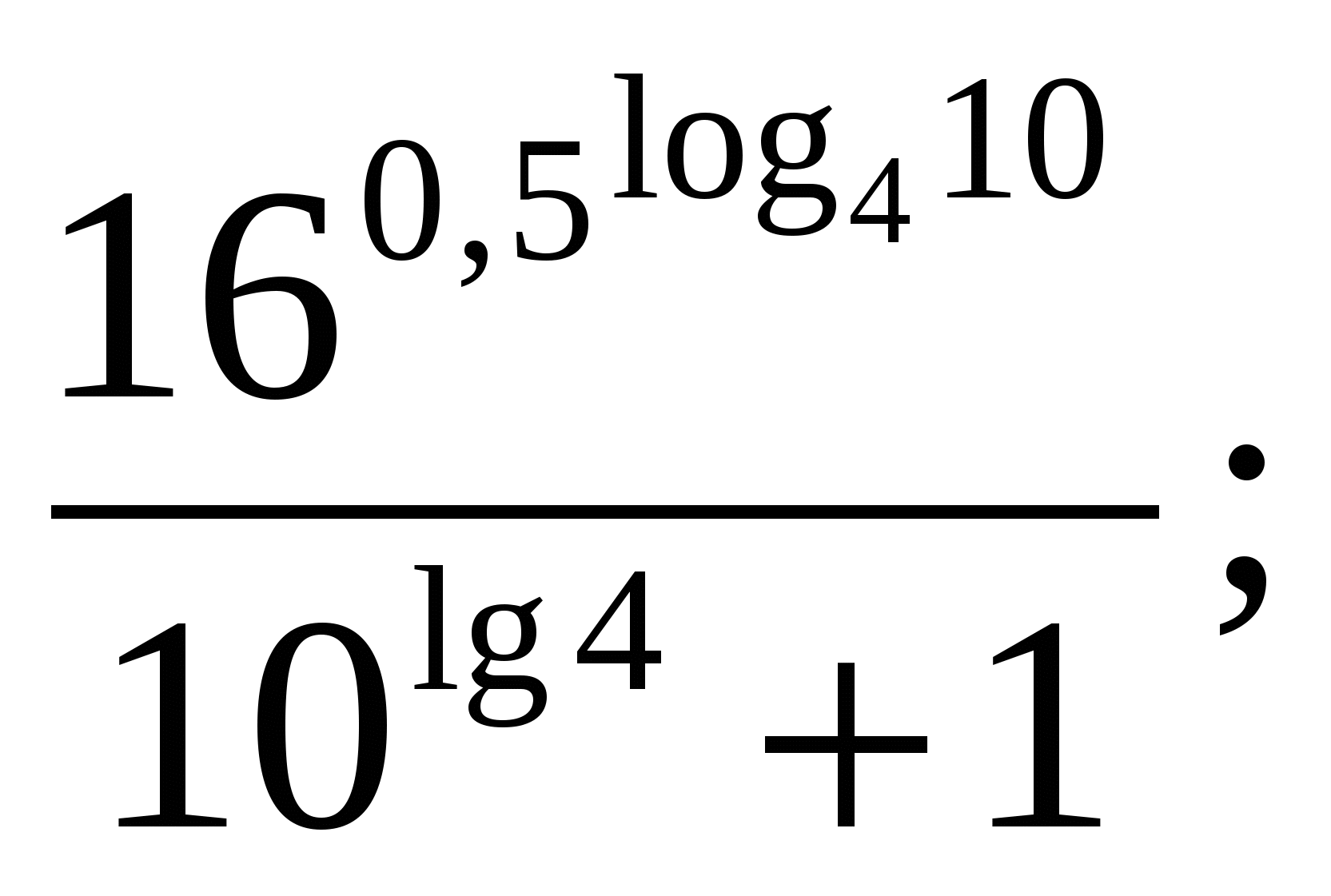
3) ![]() 4)
4) ![]()
Ответы: ![]()
Логарифмические уравнения и их системы
Справочные сведения
Определение. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение
logax = b, (1)
где a и b – данные числа, а х – переменная величина.
Если а > 0 и ![]() , то такое уравнение имеет единственный корень x = ab.
, то такое уравнение имеет единственный корень x = ab.
Решение более сложных логарифмических уравнений сводится либо к решению алгебраических уравнений, либо к решению уравнений вида (1).
Способы решения логарифмических уравнений
-
Способ непосредственного применения определения логарифма.
Пример 1. Решим уравнение logx( х3 – 5х + 10 ) = 3.
Решение. По определению логарифма можно написать: х3 – 5х + 10 = х3, откуда: х = 2.
Проверка: log2(23 - 5![]() 2 + 10) = log28 = 3. Ответ: 2.
2 + 10) = log28 = 3. Ответ: 2.
Известно, что областью определения логарифмической функции является множество положительных действительных чисел. Поэтому часто при решении логарифмических уравнений вначале определяется
область допустимых значений переменной (ОДЗ). Затем решается данное уравнение и найденные значе-ния переменной проверяются на принадлежность ОДЗ.
-
Способ приведения уравнения к виду logaf(x) = logag(x) c последующим применением потенцирования.
Пример 2. Решим уравнение: lg( x + 5) – lg( x2 – 25 ) = 0.
Решение. Найдем ОДЗ. Для этого решим систему неравенств:
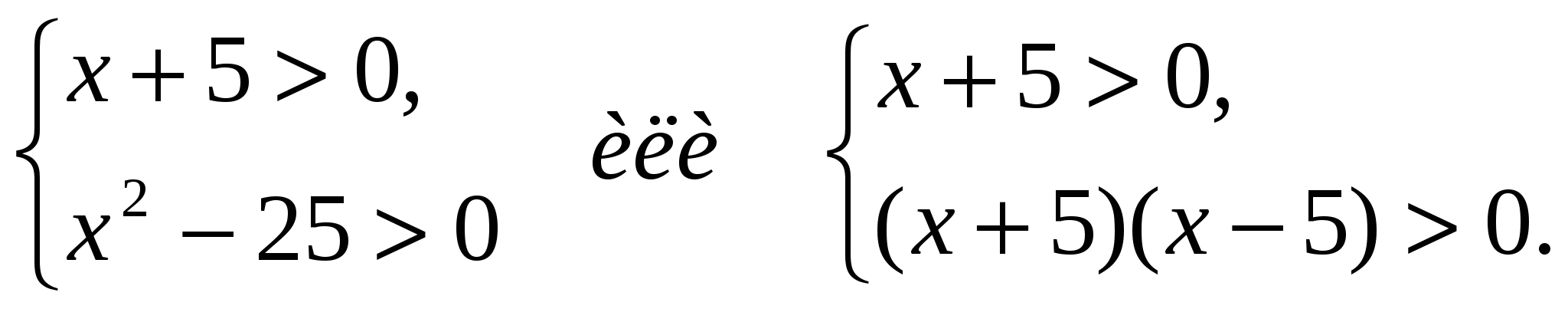 Отсюда имеем:
Отсюда имеем: ![]() .
.
Преобразуем данное уравнение: lg( x + 5) = lg( x2 – 25 ).
Потенцируя, имеем: х + 5 = х2 – 25 или х2 – х – 30 = 0, откуда х1 = 6, х2 = - 5. Но ![]() .
.
Ответ: 6.
-
Способ введения новой переменной.
Пример 3. Решим уравнение :![]()
Решение. Пусть log2 х = у, тогда вместо исходного уравнения получим: у2 – у – 2 = 0.
Решив полученное квадратное уравнение, имеем: у1 = 2, у2 = - 1.
Теперь найдем искомые значения х:
log2 х = 2, х1 = 4; log2 х = -1, х2 = ![]() .
.
ОДЗ: х > 0. Оба найденные значения х принадлежат ОДЗ. Ответ: 4; ![]() .
.
-
Способ почленного логарифмирования.
Пример 4. Решим уравнение: ![]()
Решение. Перепишем это уравнение в следующем виде: ![]() или
или ![]()
Теперь почленно прологарифмируем это уравнение по основанию 2:
![]() . Применяем свойства логарифмов:
. Применяем свойства логарифмов: ![]()
![]()
![]()
Решаем это уравнение способом введения новой переменной. Получаем:
1) log2 х = 3, х1 = 8; 2) log2 х = -1, х2 = ![]() .
.
Выполняем проверку:
-
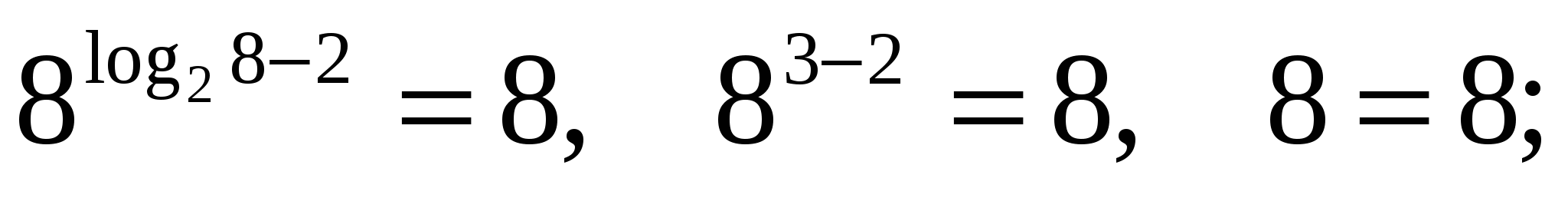
-
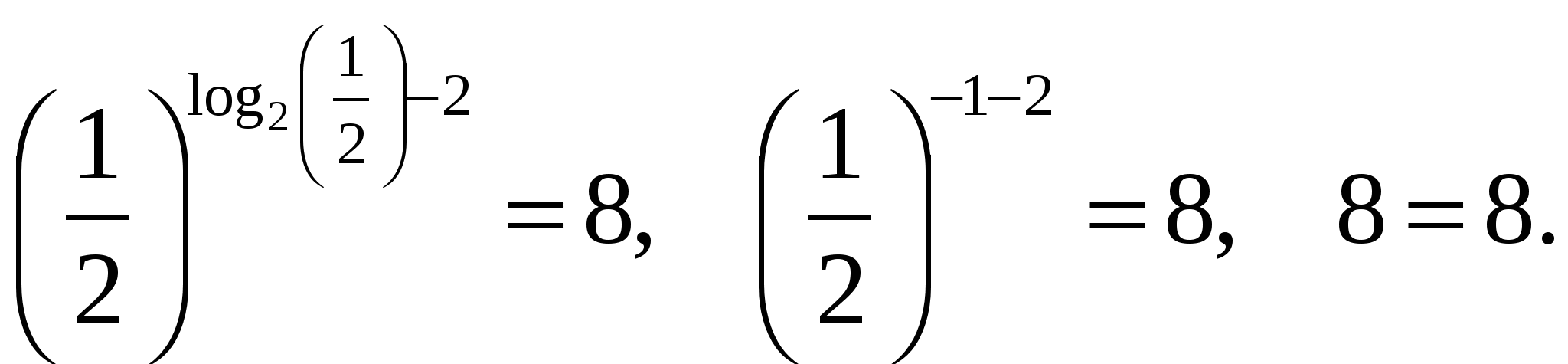 Ответ: 8;
Ответ: 8; 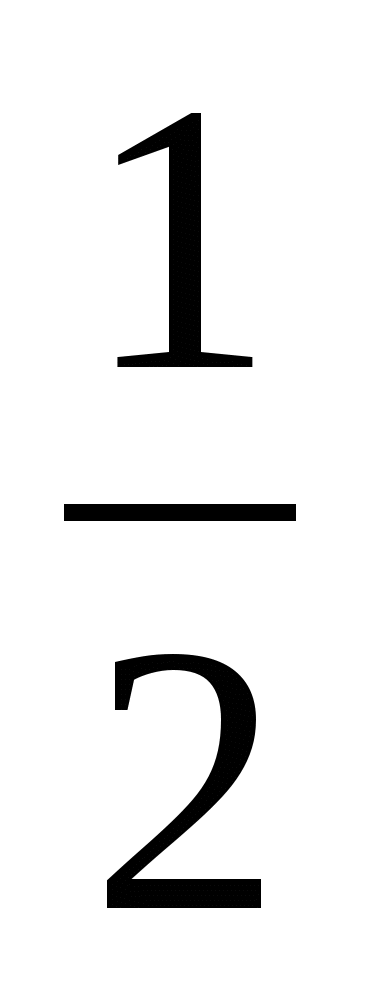 .
.
-
В практике встречаются логарифмические уравнения, содержащие логарифмы с разными
основаниями. В таких случаях применяется формула перехода к новому основанию:
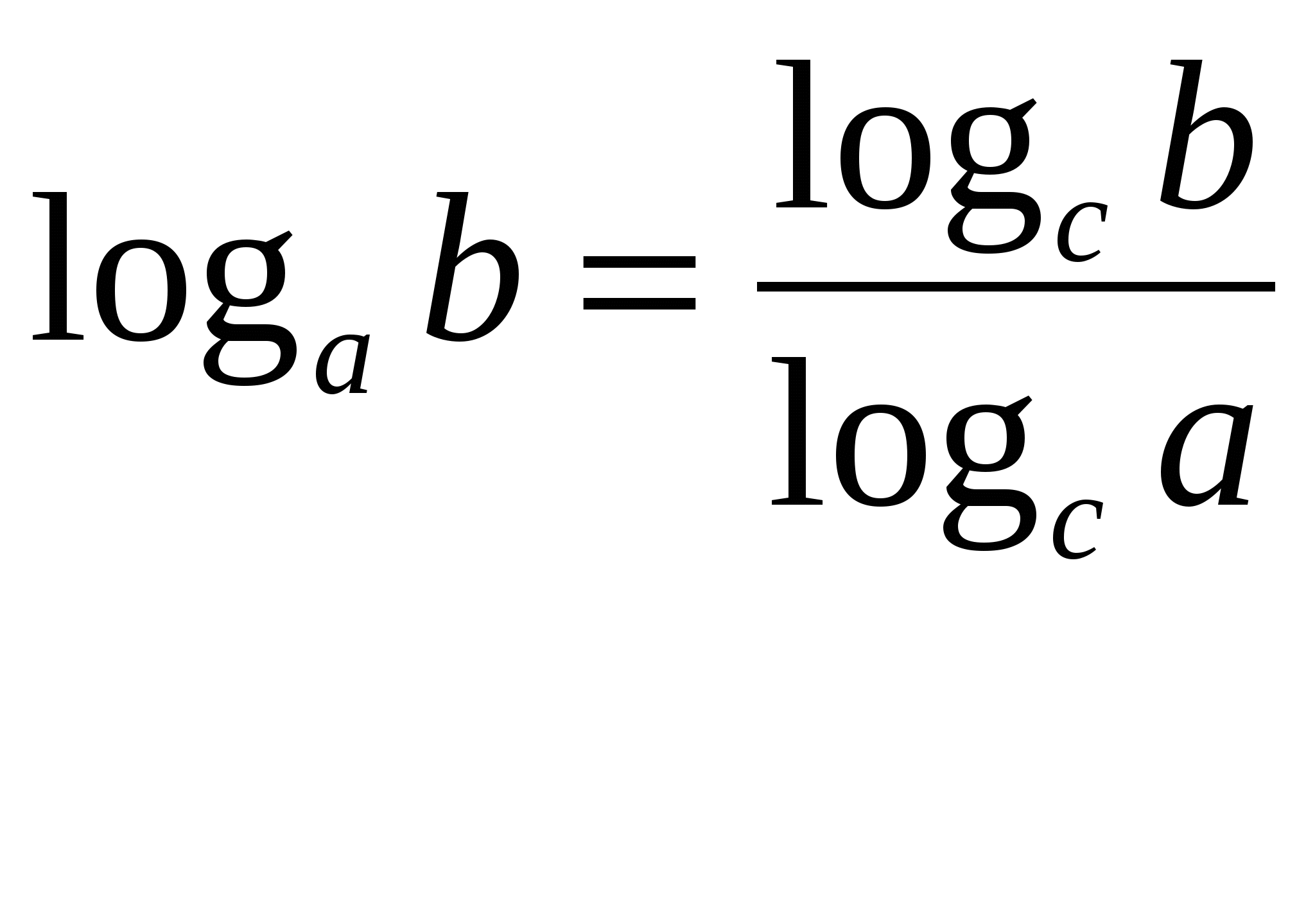
Пример 5. Решим уравнение: ![]()
Решение. ОДЗ: ![]()
Используем формулу перехода к новому основанию: ![]() тогда данное
тогда данное
уравнение имеет вид: 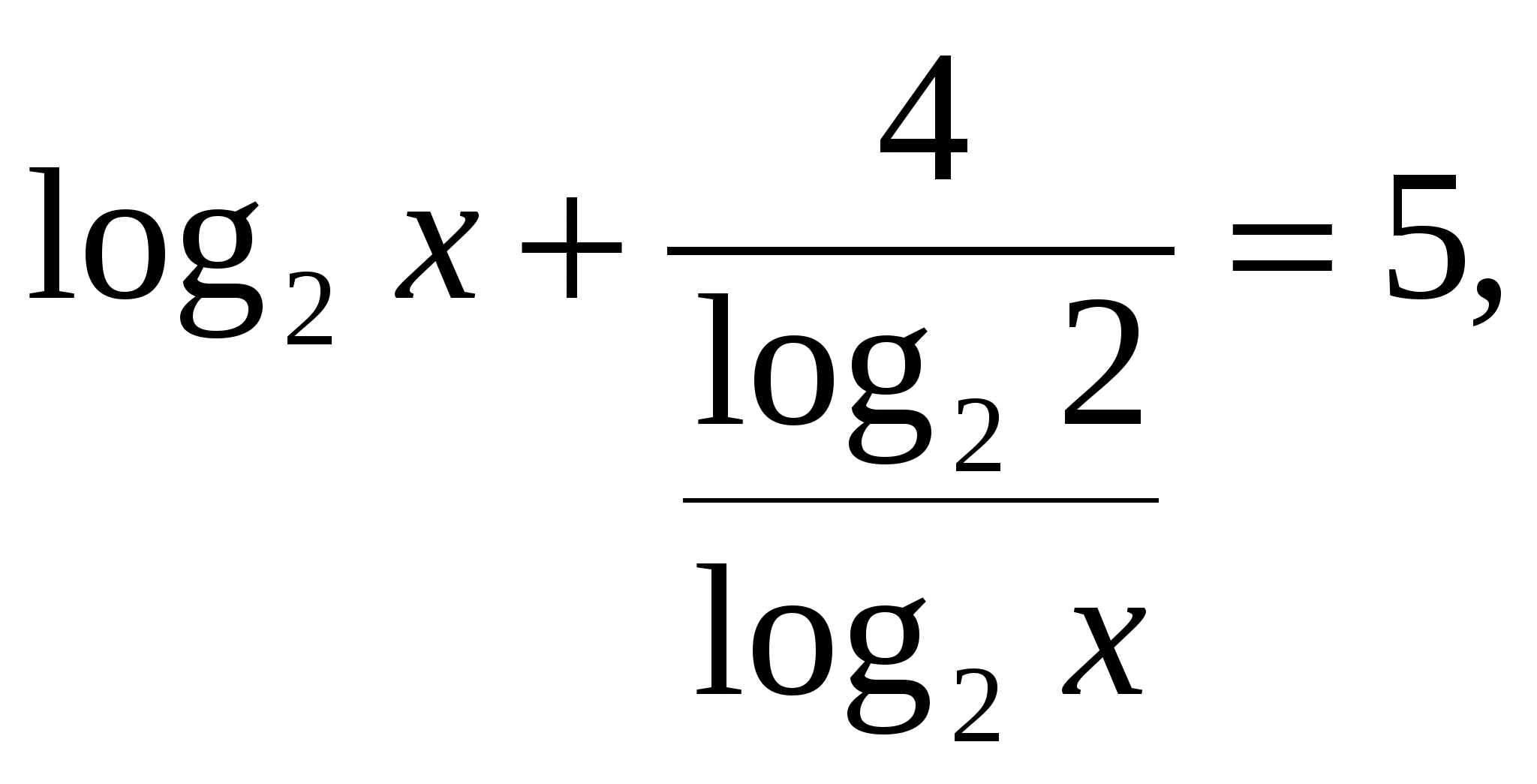 или
или ![]()
Тогда: ![]()
![]() откуда получаем, что х = 2.
откуда получаем, что х = 2.
![]() Ответ: 2.
Ответ: 2.
-
Показательно-логарифмические уравнения.
Чаще всего такие уравнения решаются способом логарифмирования обеих частей уравнения и приведением к логарифмическим уравнениям.
Пример 6. Решим уравнение: ![]()
Решение. Перепишем это уравнение в виде: ![]() Воспользуемся
Воспользуемся
основным логарифмическим тождеством ![]() , имеем:
, имеем:
![]()
![]()
![]()
Прологарифмируем обе части уравнения по основанию 3: ![]() Тогда
Тогда
![]() откуда:
откуда: ![]() и
и ![]() или х1 =
или х1 = ![]() и х2 = 9.
и х2 = 9.
Проверка:![]()
![]() Ответ:
Ответ: ![]()
При решении систем логарифмических уравнений в основном применяются те же способы, что и при решении систем алгебраических уравнений ( способы подстановки, алгебраического сложения, введения новых переменных и др.)
Пример 6. Решим систему уравнений: 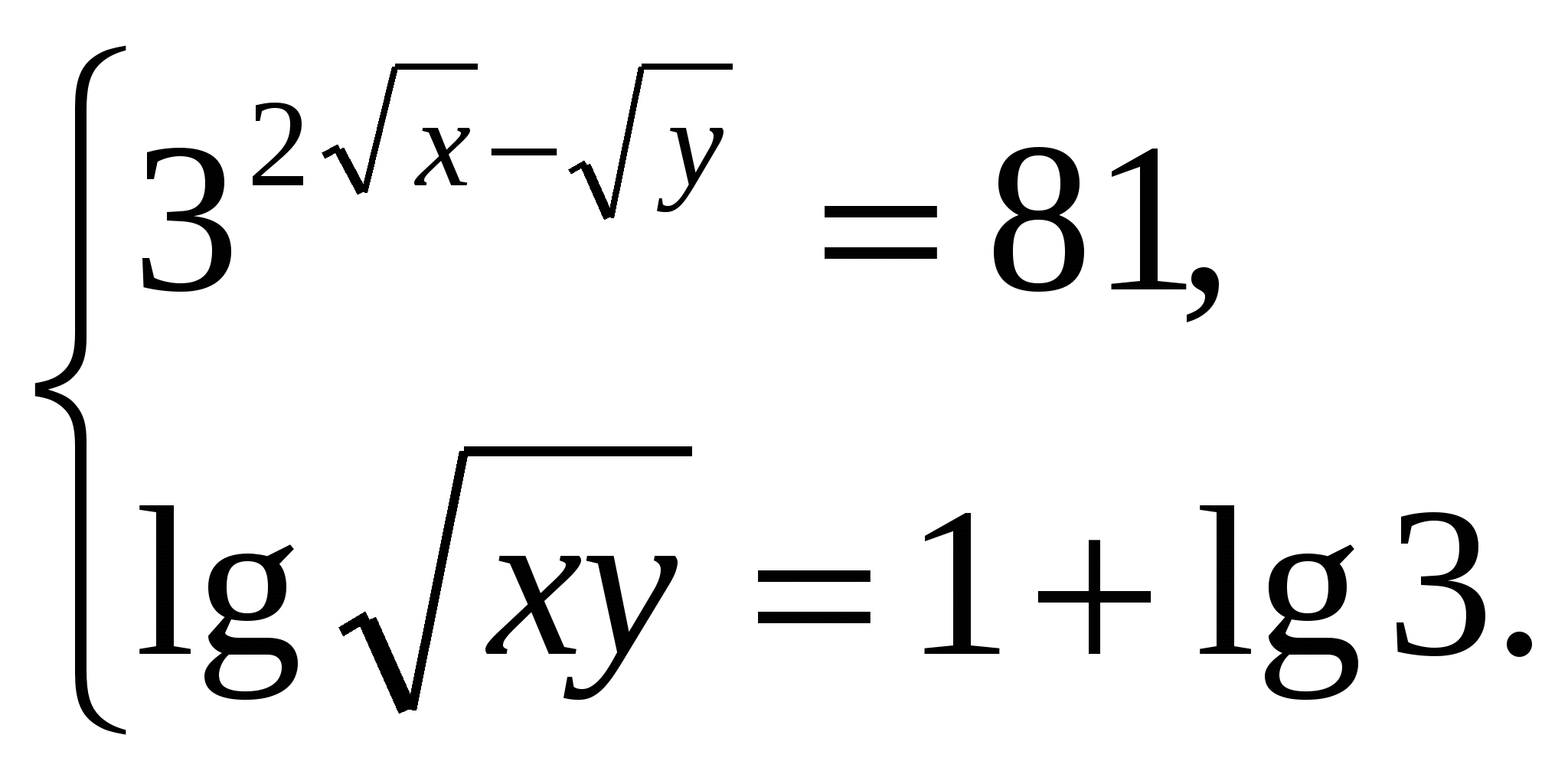
Решение. Для первого уравнения применяем свойства показательной функции, а второе
уравнение потенцируем: 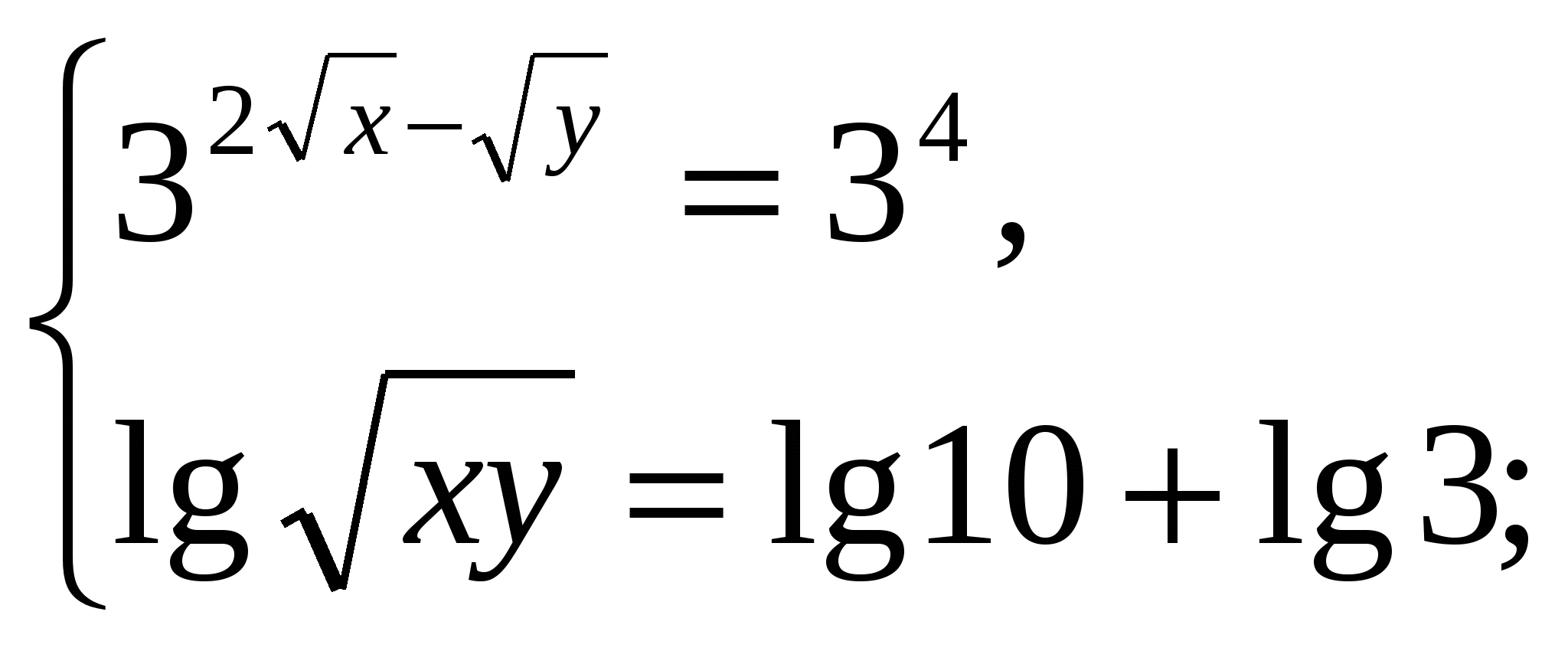
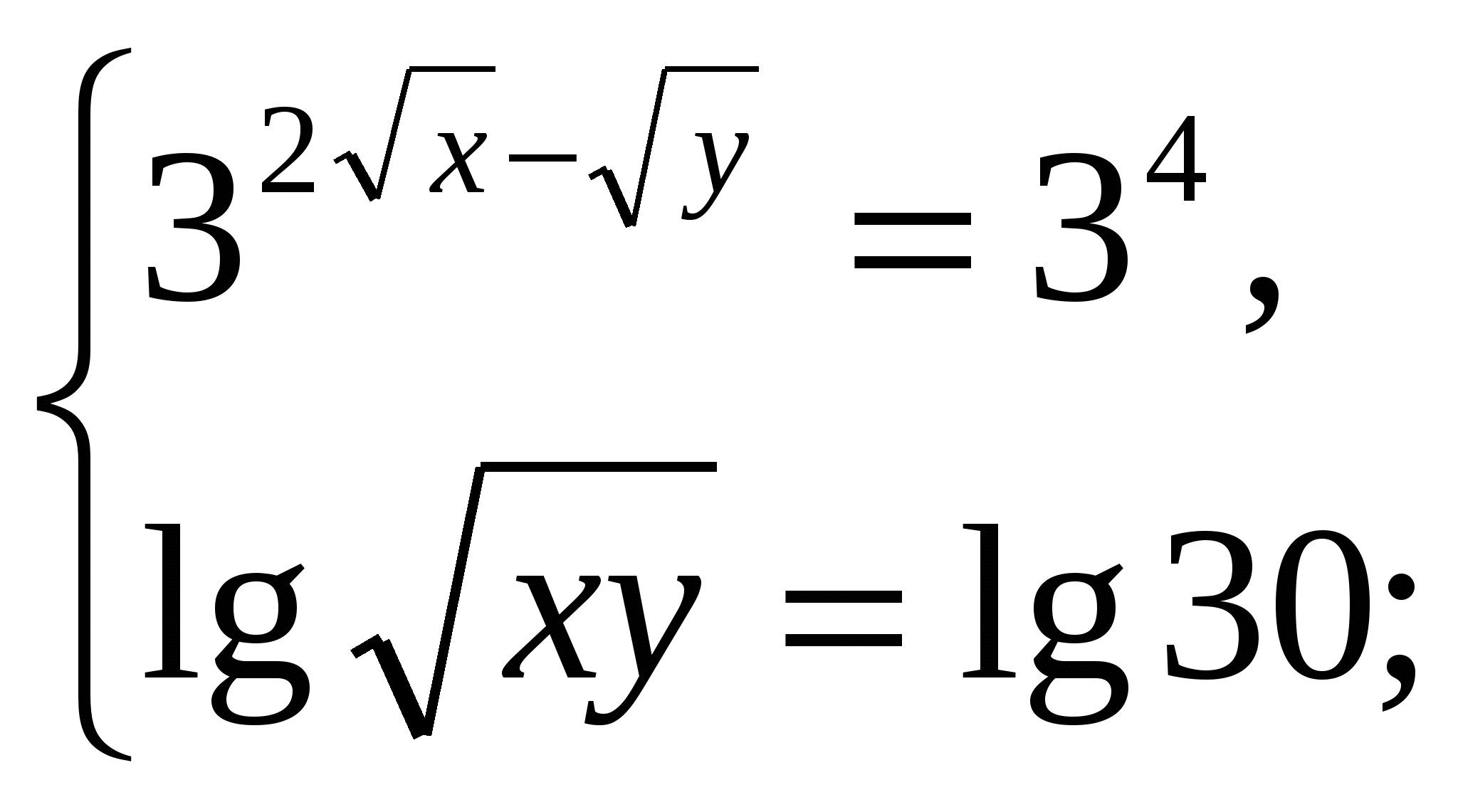
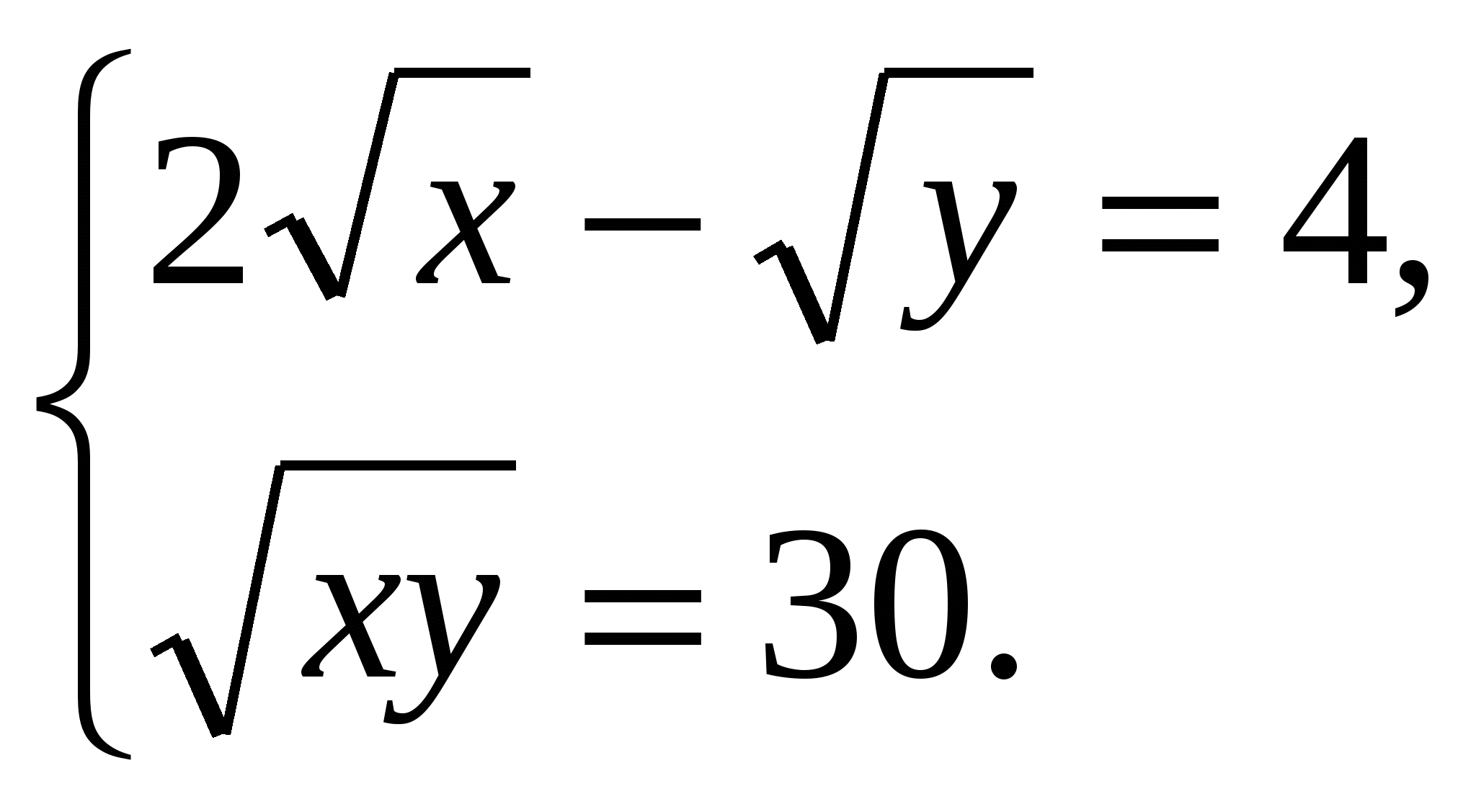
Введем новые переменные:
![]() получим систему рациональных уравнений:
получим систему рациональных уравнений: 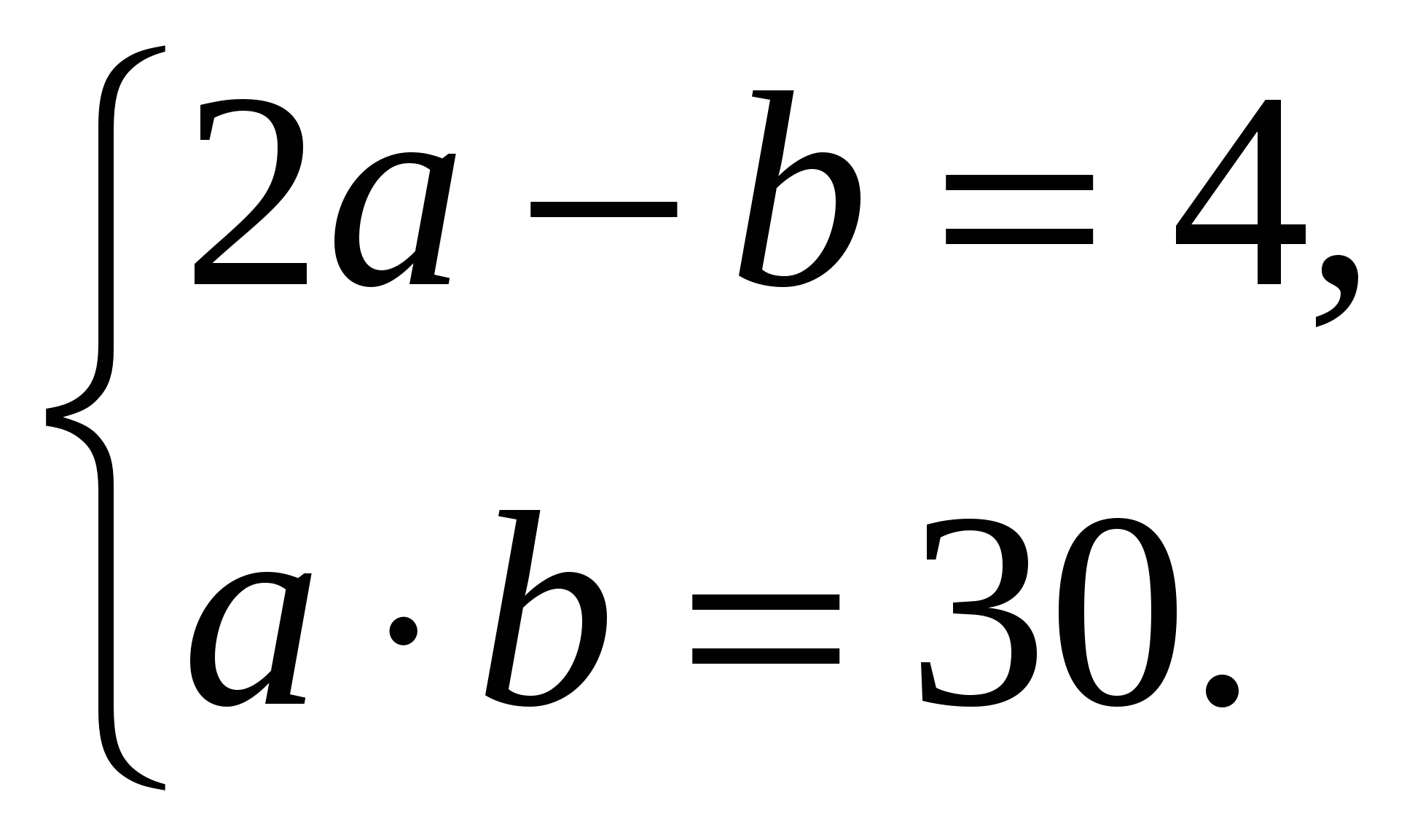
Решаем систему методом подстановки, получаем: а = 5 и b = 6. Тогда: ![]()
или х = 25 и у = 36.
Проверка: 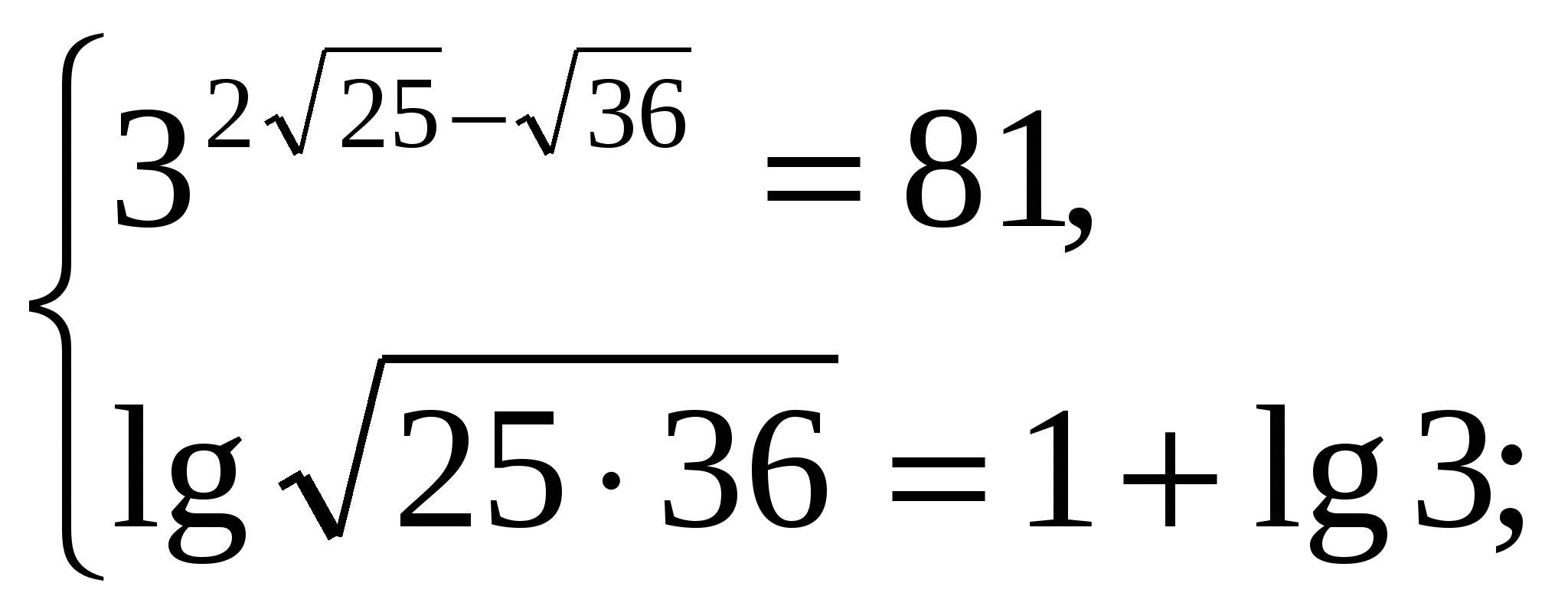
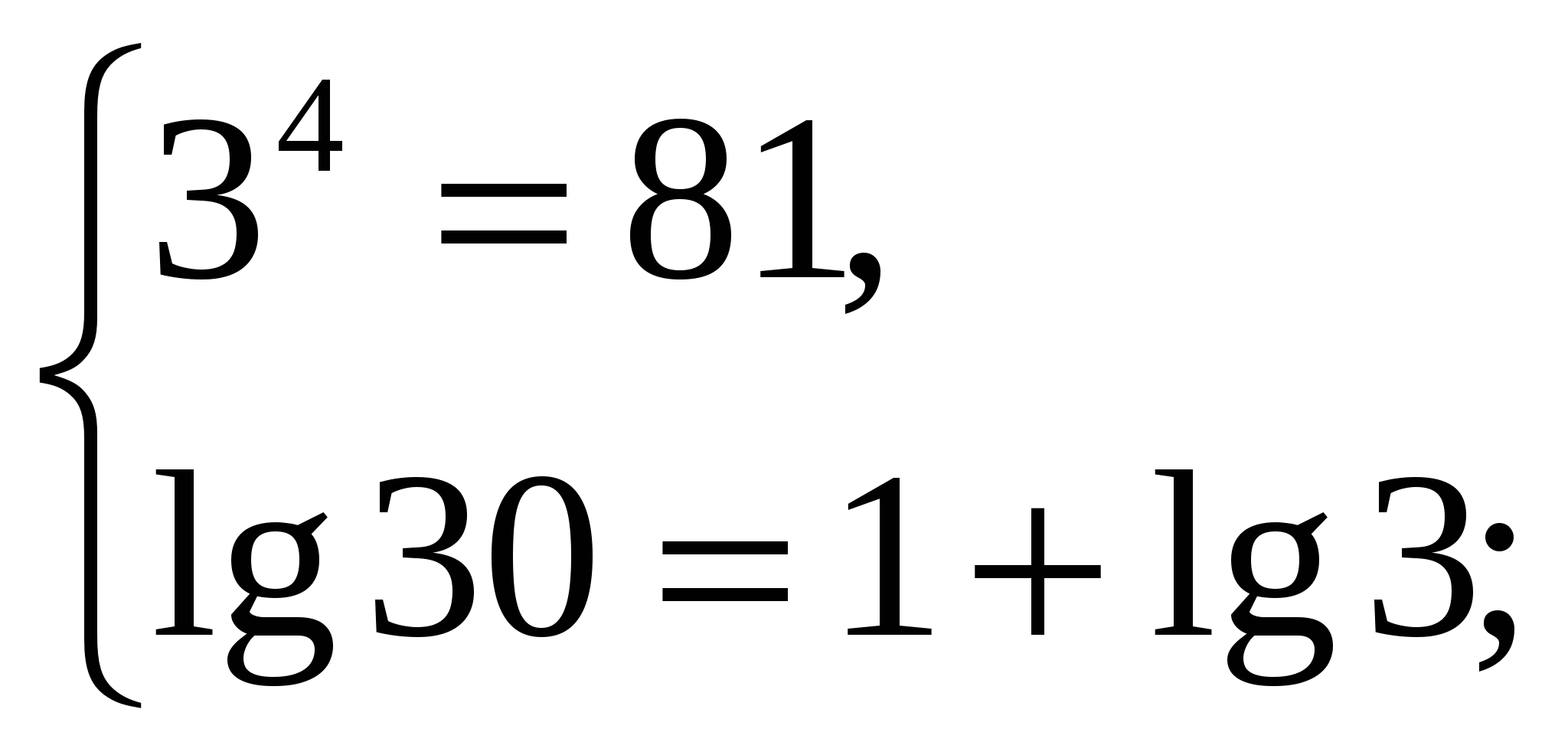
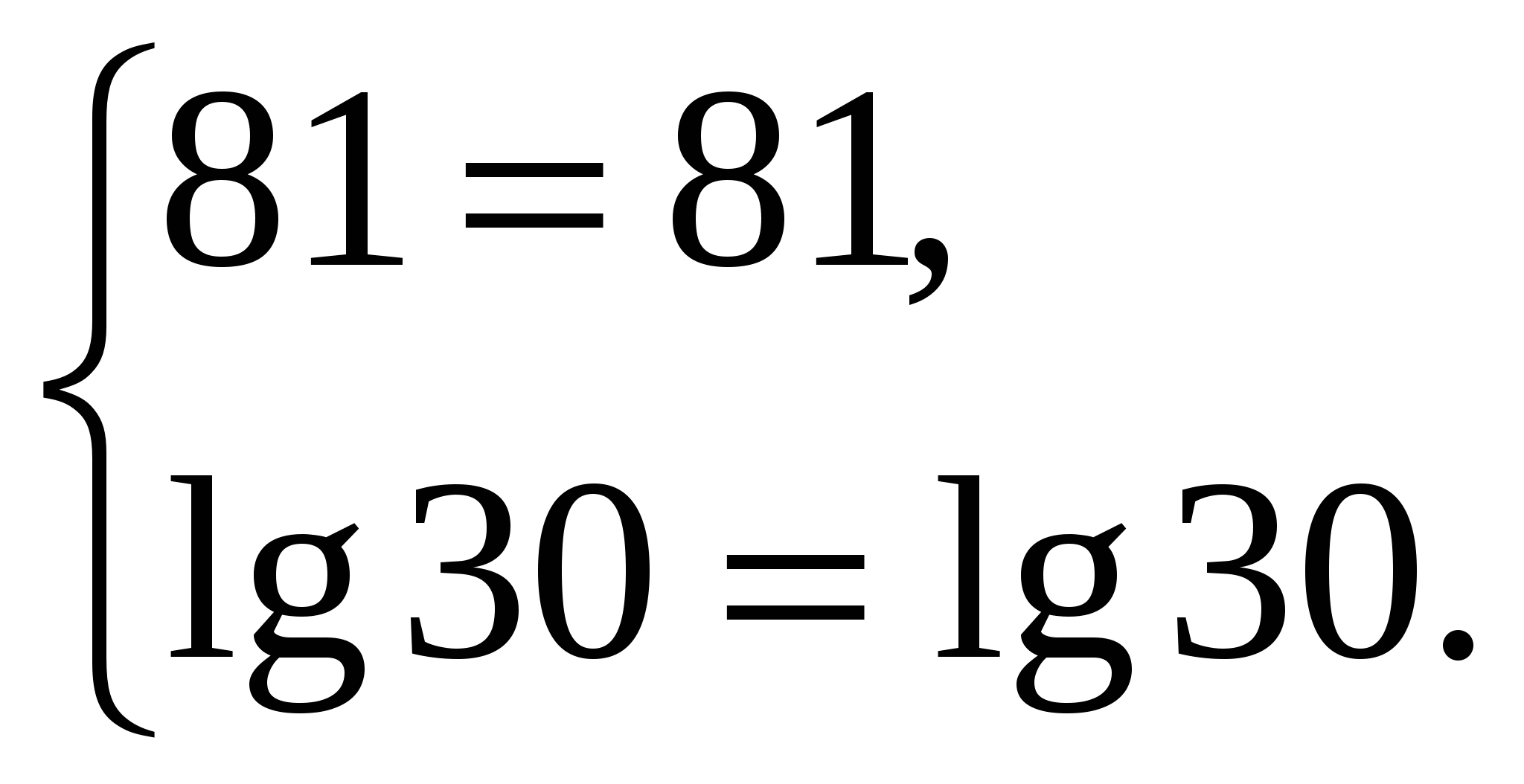
Вывод: пара чисел (25;36) действительно является решением системы.
Ответ: (25;36).
Дидактический материал
-
Решите логарифмические уравнения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Решите системы логарифмических уравнений:
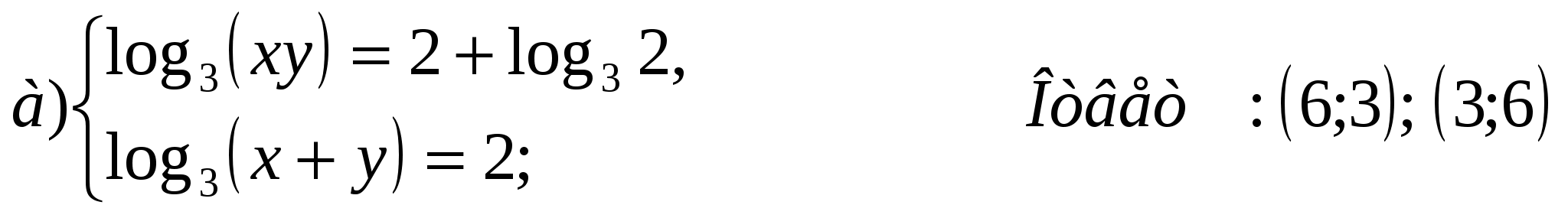
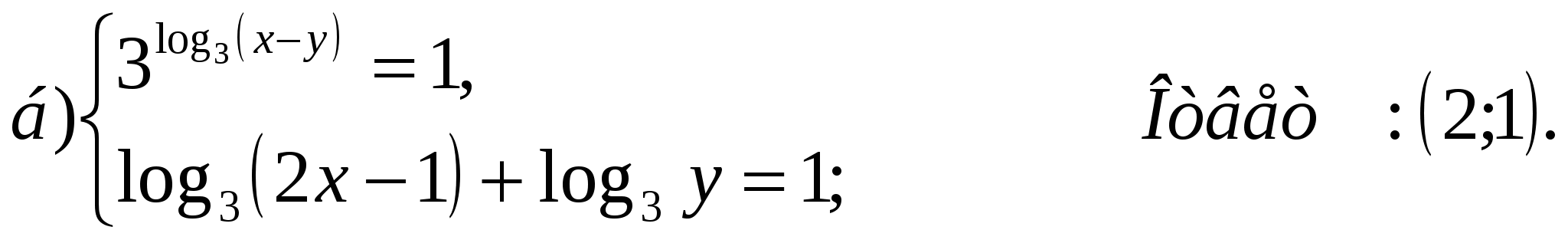

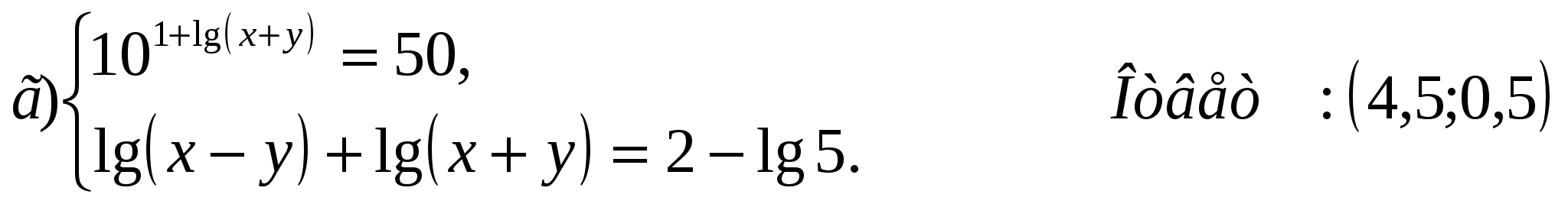
Логарифмические неравенства
Справочные сведения
Определение. Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим неравенством.
Всякое значение переменной , при котором данное логарифмическое неравенство обращается в
верное числовое неравенство, называется решением логарифмического неравенства.
Решить логарифмическое неравенство – значит найти все его решения или доказать, что их нет.
Решение логарифмических неравенств в основном сводится к решению неравенств вида
![]() или
или ![]()
Для решения таких неравенств, учитывая область определения логарифмической функции и ее свойства, применяют следующие утверждения:
-
при а > 1 неравенство
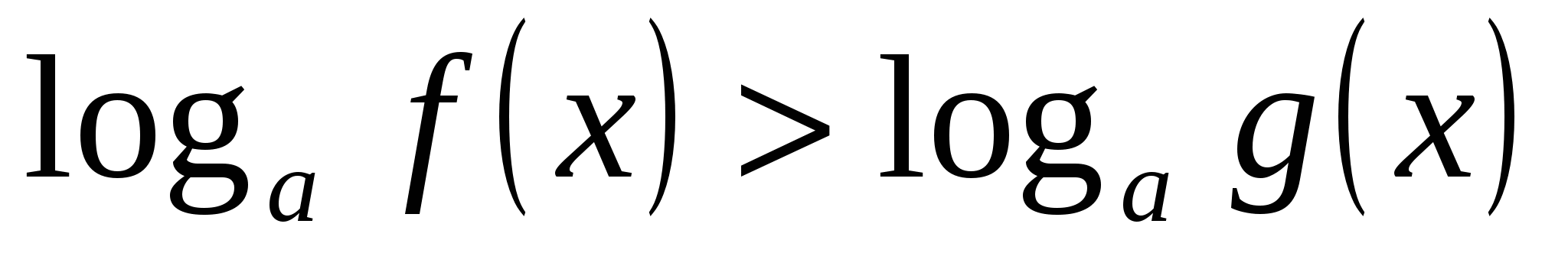 равносильно системе неравенств:
равносильно системе неравенств:
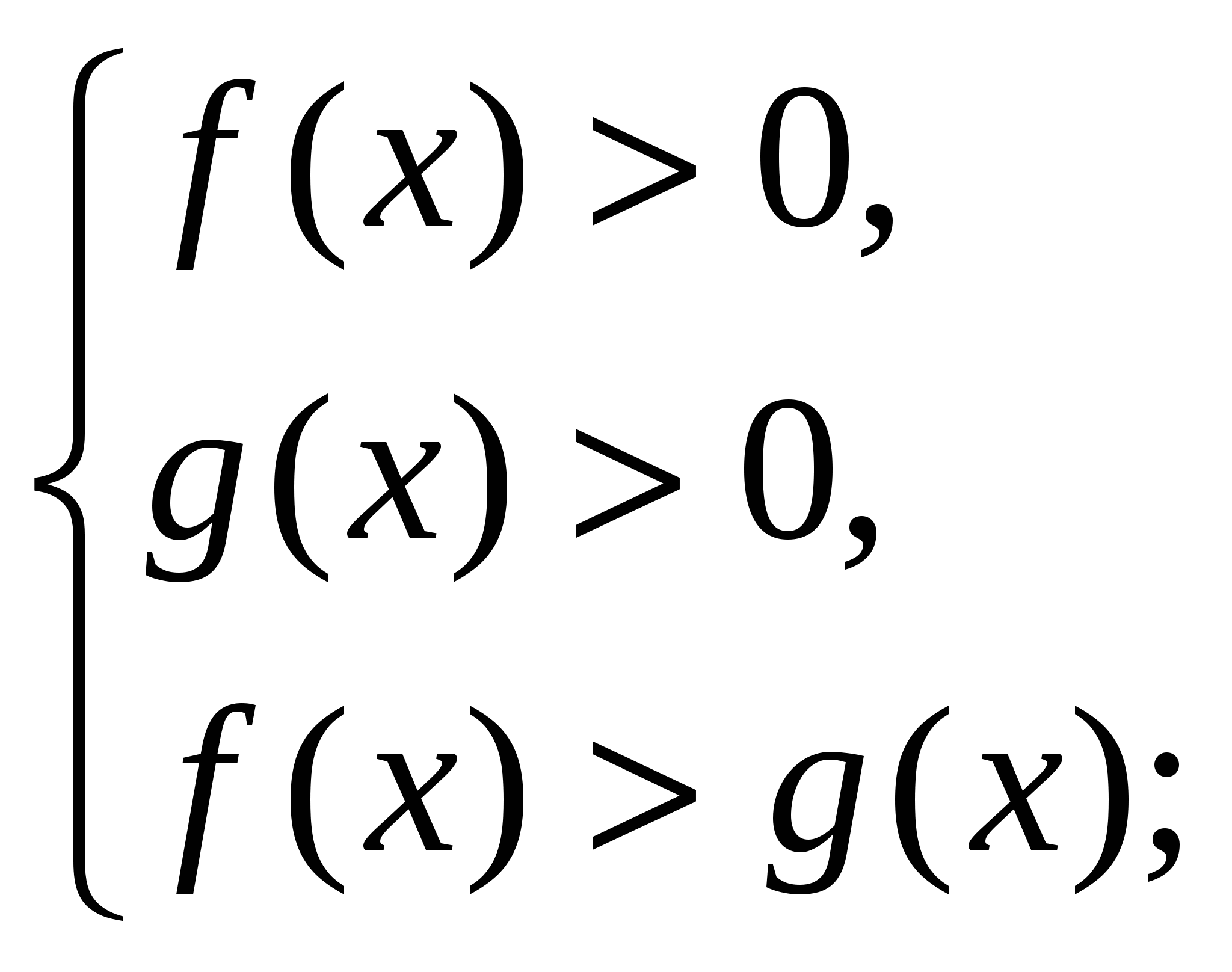 (1)
(1)
-
при 0 1 неравенство
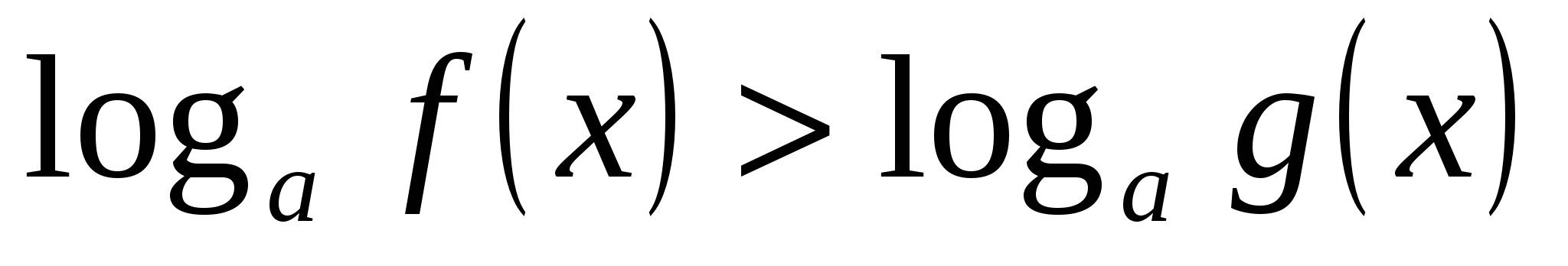 равносильно системе неравенств:
равносильно системе неравенств:
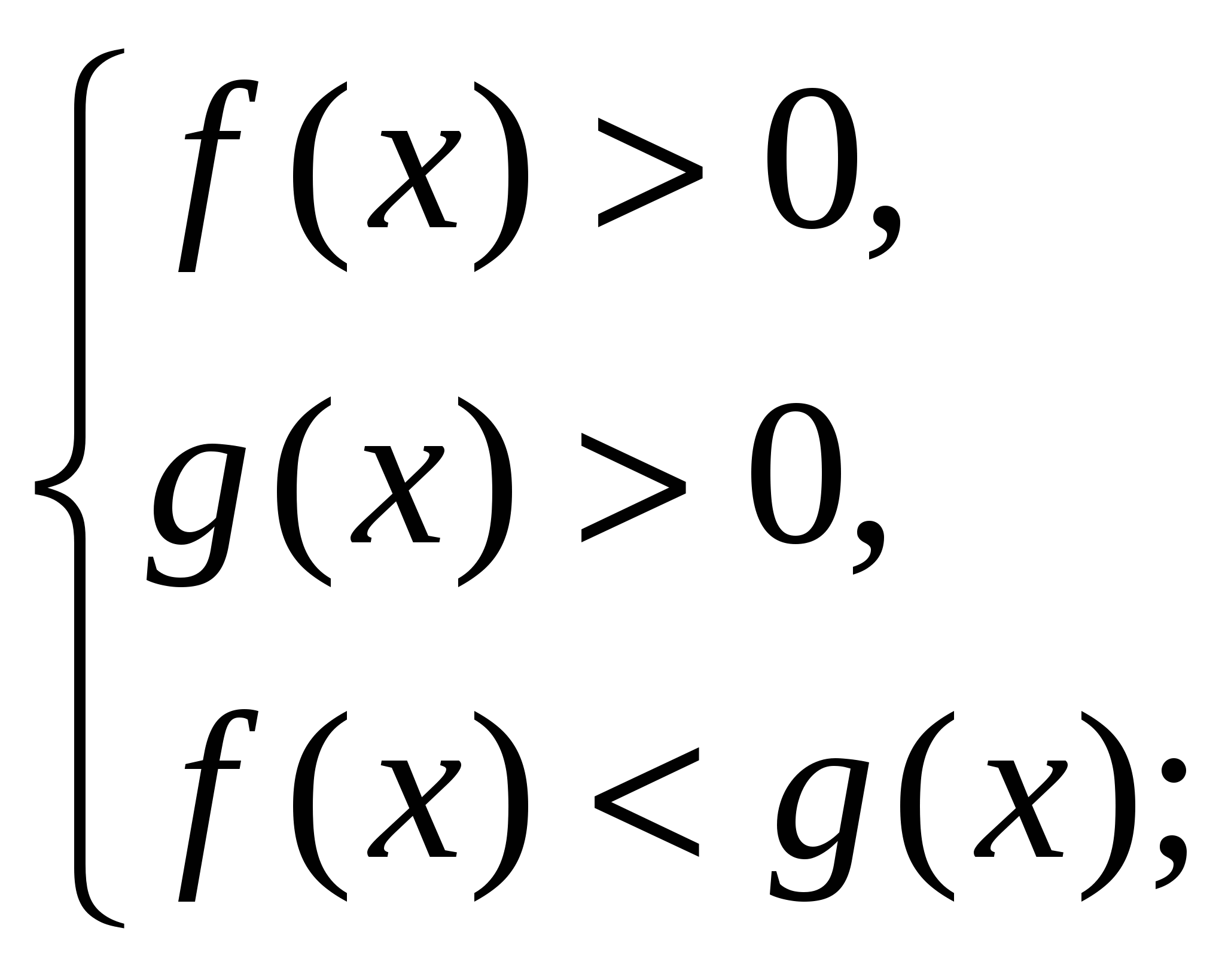 (2)
(2)
Примеры с решениями
Пример 1. Решим неравенство ![]()
Решение. Преобразуем правую часть неравенства: ![]() Здесь а =
Здесь а = ![]() , поэтому
, поэтому
используем систему неравенств вида (2): 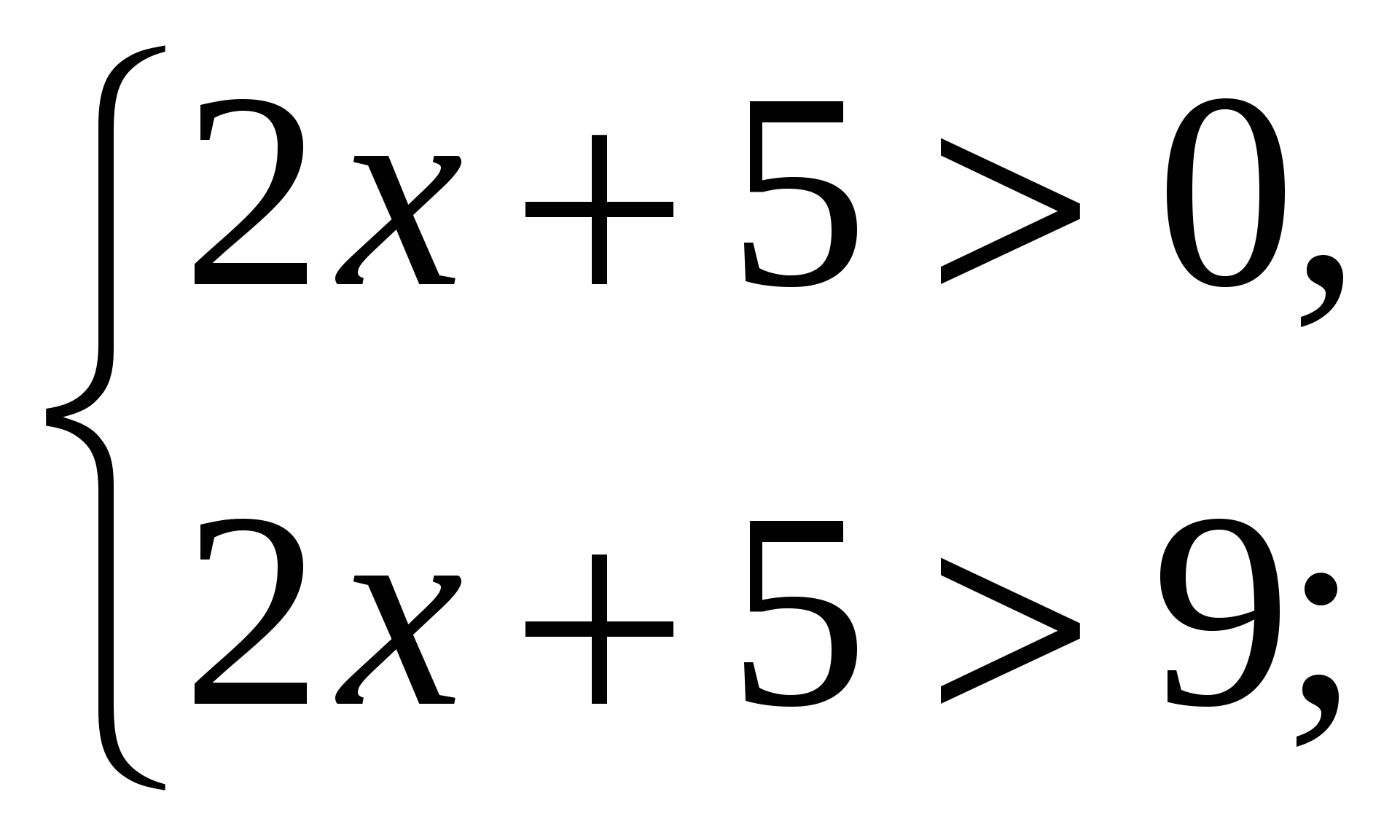 или
или 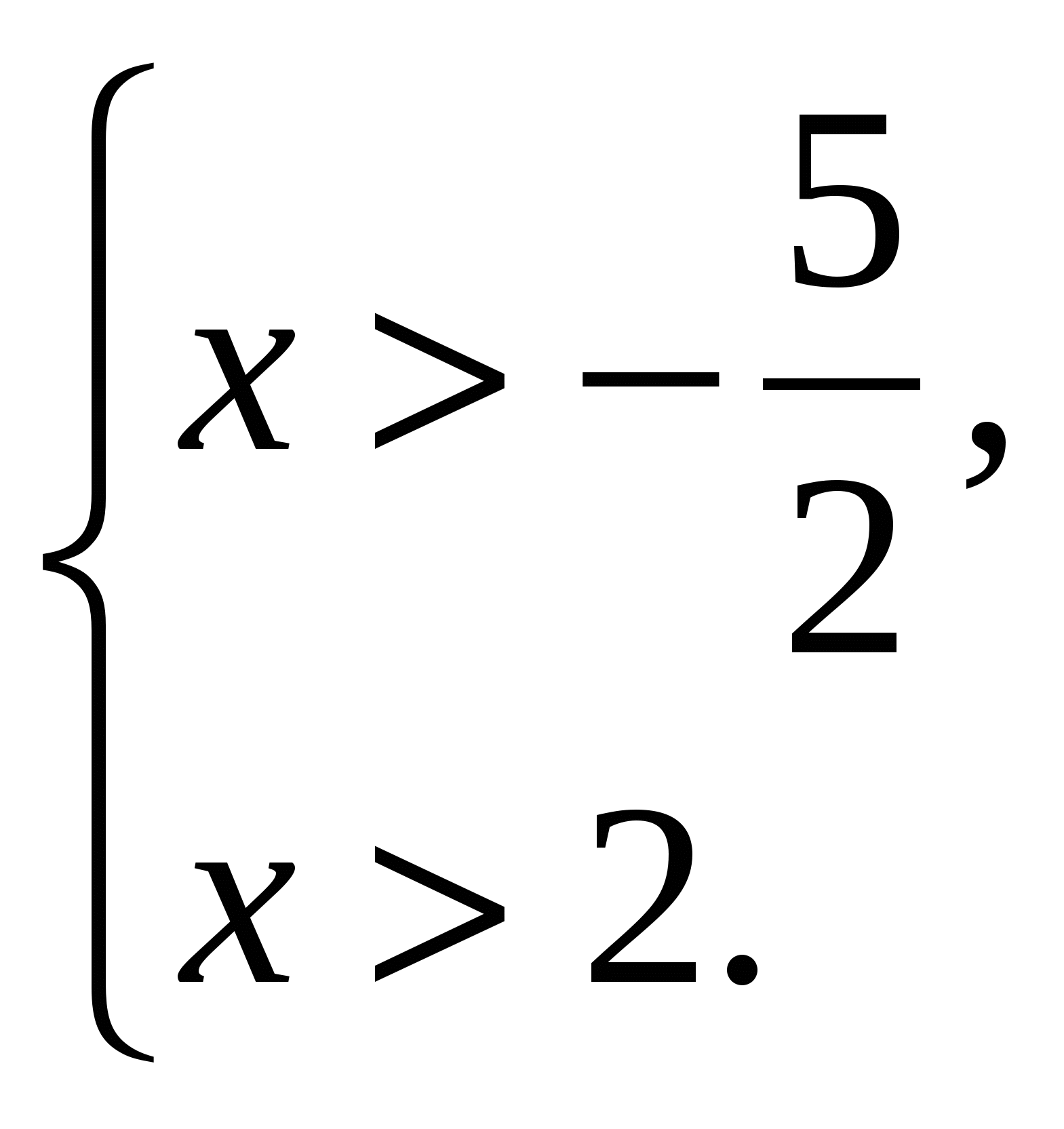
Решением последней системы будет промежуток ![]() Ответ:
Ответ: ![]()
Пример 2. Решим неравенство ![]()
Решение. Используем свойства логарифмов: ![]()
![]()
В полученном неравенстве а = 10 > 1, поэтому используем систему неравенств вида (1):
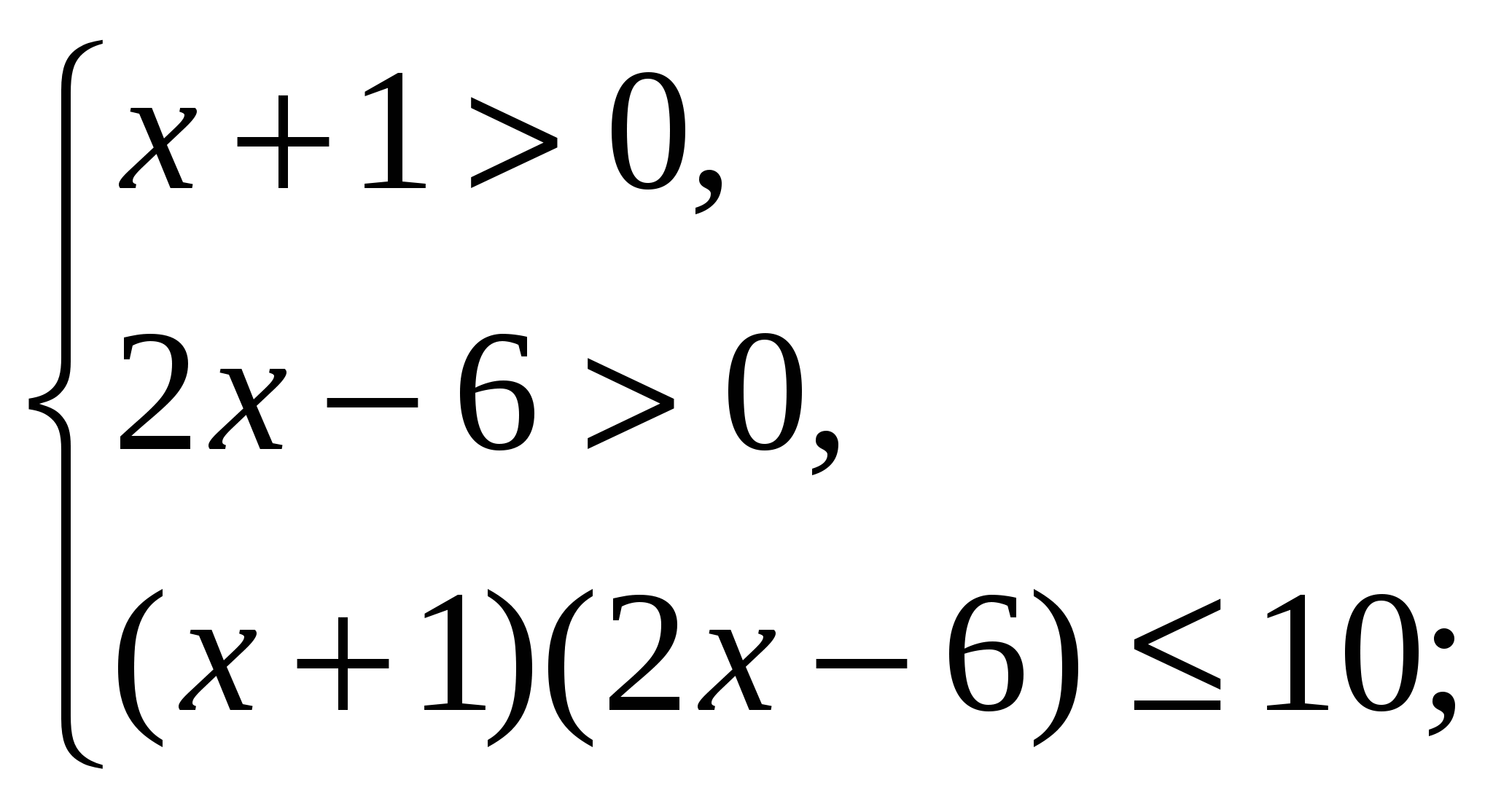 отсюда:
отсюда: 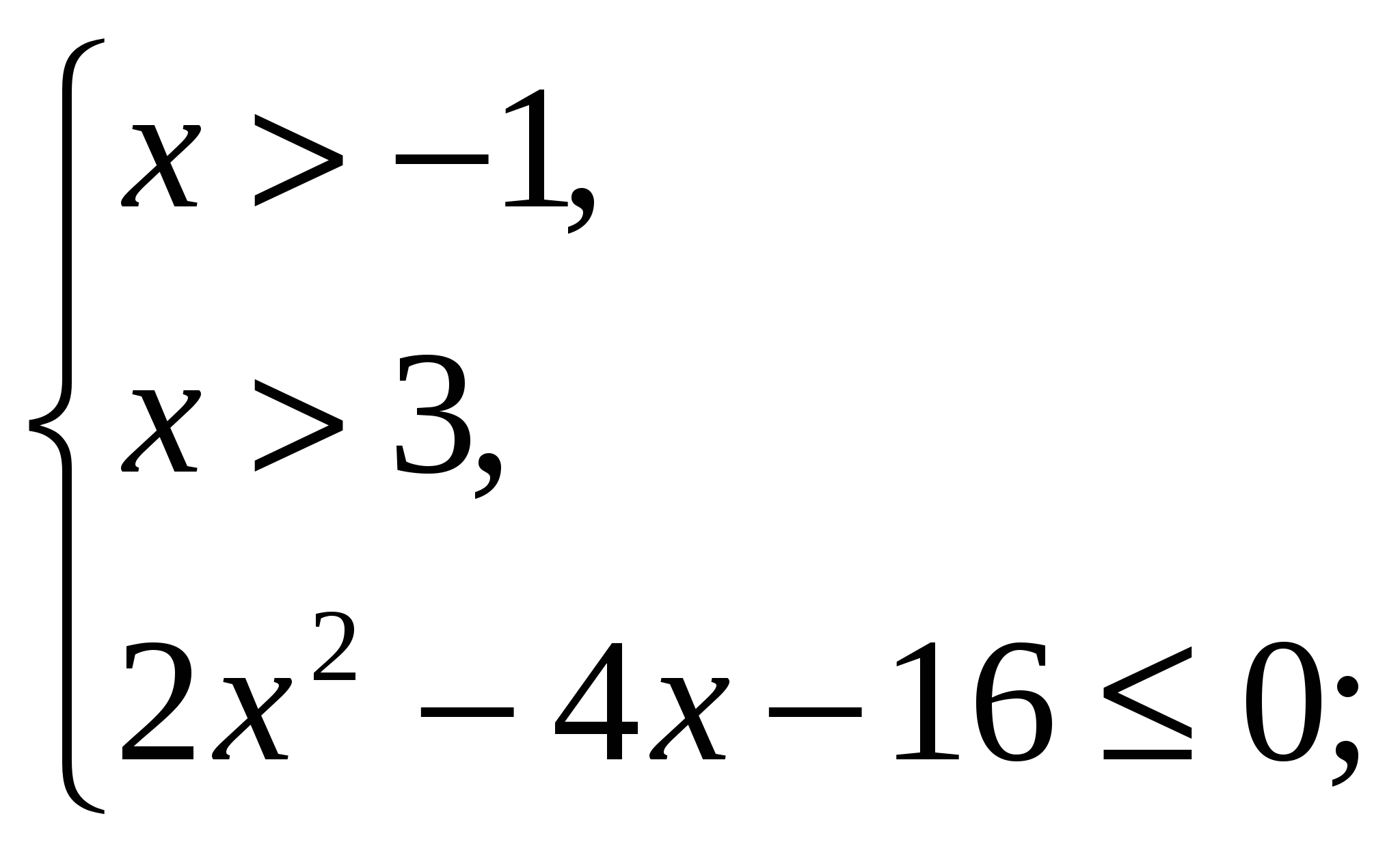
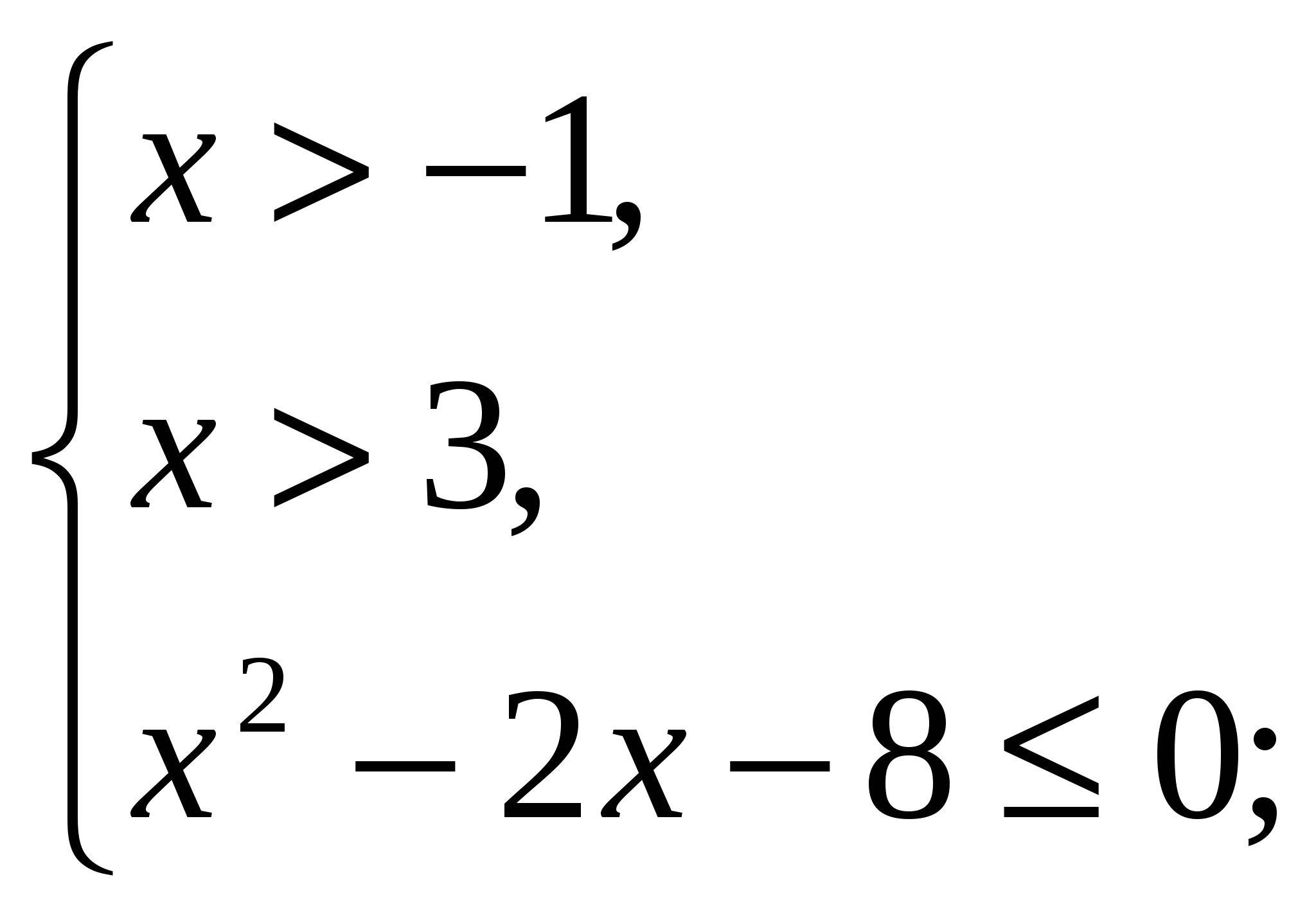
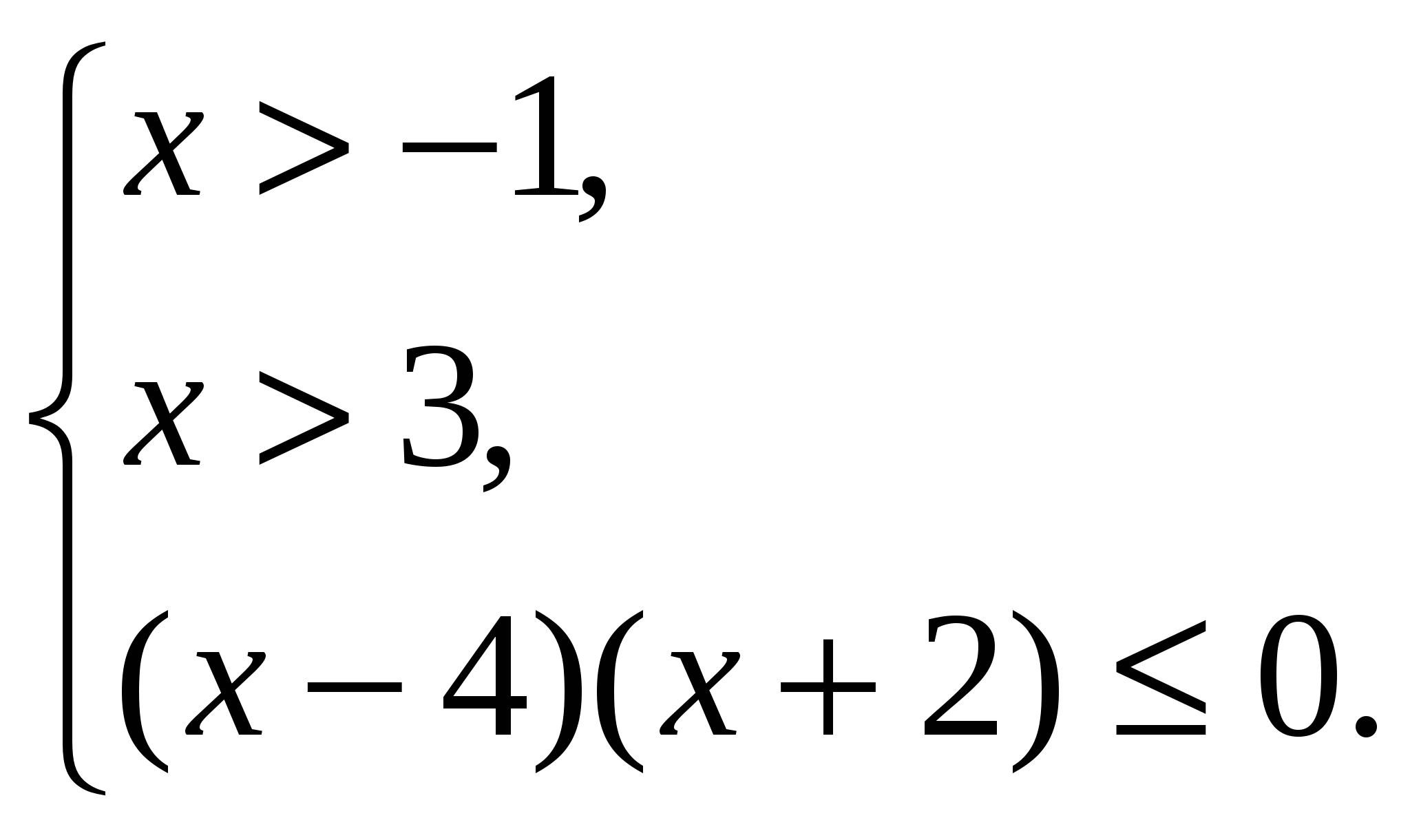
Изображая решение каждого неравенства системы по отдельности на координатной прямой, находим общую часть – промежуток ![]() Ответ:
Ответ: ![]()
Дидактический материал
-
Решите логарифмические неравенства:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тест № 1
| Вычислите: | |
| |
|
| 2. | Найти значение выражения: |
| |
|
| 3. | Решите уравнение: |
| |
|
| 4. | Решите неравенство: |
| |
|
| 5. | Решить систему уравнений |
| |
|
| 6. | Решите уравнение: |
| |
|
| 7. | Найдите произведение корней уравнения |
| |
|
| 8. | Решите неравенство: |
| |
|
| 9. | Решите неравенство: |
| |
|
| 10. | Решить систему уравнений: |
| |
|
Тест № 2
| Вычислите : | ||
| |
| |
| 2. | Используя определение и свойства логарифмов, найдите значение выражения:
| |
| |
| |
| 3. | Решите уравнение: | |
| |
| |
| 4. | Решить неравенство: | |
| |
| |
| 5. | Решить систему уравнений | |
| |
| |
| 6. | Решите уравнение: | |
| |
| |
| 7. | Найдите произведение корней уравнения: | |
| |
| |
| 8. | Решите неравенство: | |
| |
| |
| 9. | Решите неравенство: | |
| |
| |
| 10. | Решить систему уравнений | |
| |
| |
Тест № 3*
| Найти значение выражения: | |
| |
|
| 2. | Чему равно выражение: |
| |
|
| 3. | Решите уравнение: |
| |
|
| 4. | Решите уравнение: |
| |
|
| 5. | Решить систему неравенств: |
| |
|
| 6. | Найдите |
| |
|
| 7. | Вычислите: |
| |
|
| 8. | Решите уравнение: |
| |
|
| 9. | Решите неравенство: |
| |
|
| 10. | Решить систему неравенств: |
| |
|
Код правильных ответов по теме «Логарифмы»
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Тест № 1 | C | E | D | E | B | C | E | D | C | B |
| Тест № 2 | D | E | C | D | A | C | C | E | D | D |
| Тест № 3* | C | A | A | E | E | E | A | A | E | E |
Здесь представлен конспект к уроку на тему «Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.