Презентация "Свойство биссектрисы угла" (8 класс) по математике – проект, доклад
Презентацию на тему "Свойство биссектрисы угла" (8 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
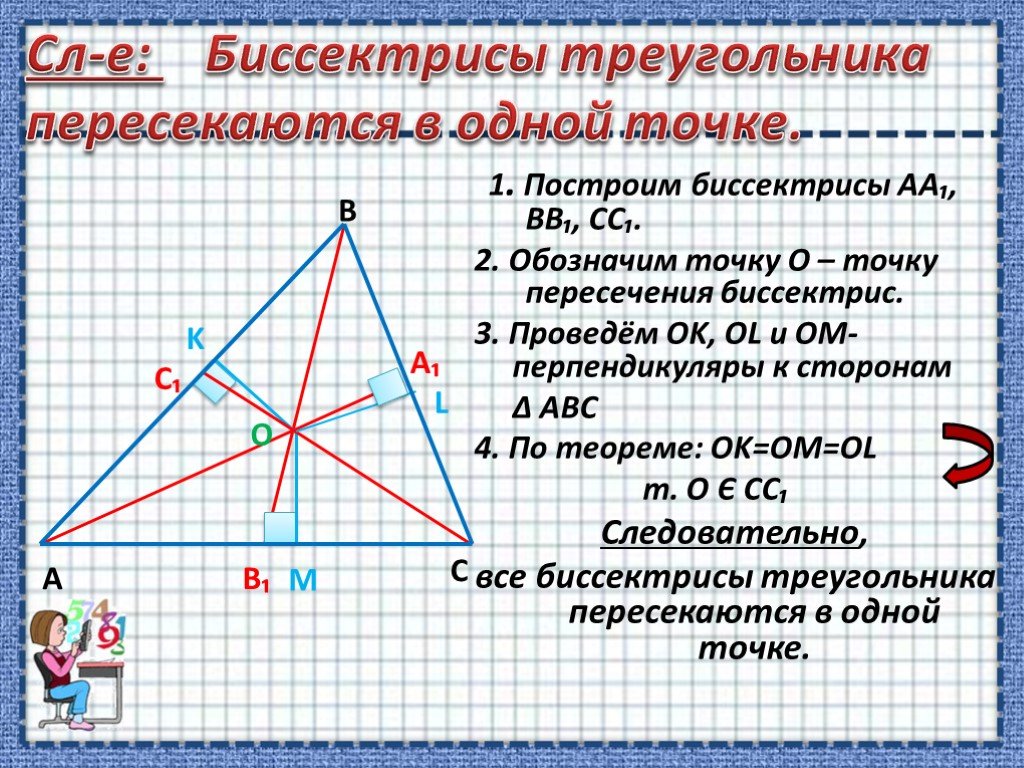
Свойство точек биссектрисы угла
Основополагающий вопрос. - Как расположены точки биссектрисы угла от его сторон? - Какой фигурой будет геометрическое место точек, равноудалённых ...Свойство биссектрисы равнобедренного треугольника
Повторение. Треугольник, у которого 2 стороны равны, называется равнобедренным треугольником. D С E B A C H M. DM – медиана треугольника АDВ. AM = ...Свойство биссектрисы
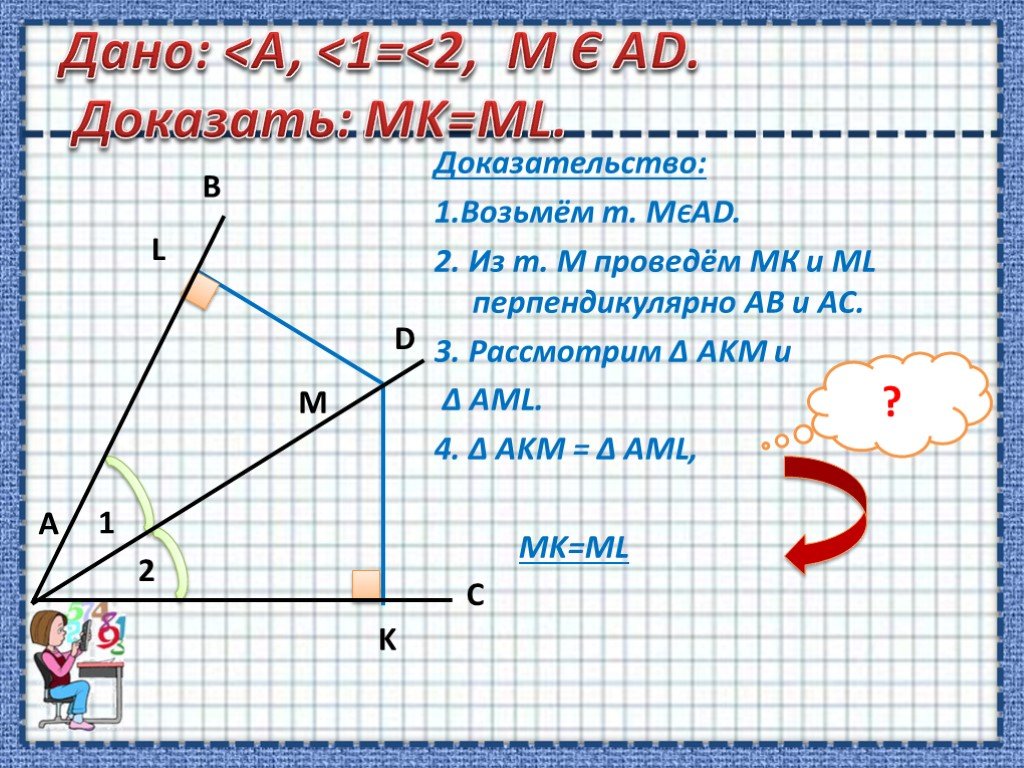
Цели урока:.Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Учить применять данные теоремы и следствие при решении задач. Исторически ...
Свойства биссектрисы угла
Тип урока: урок усвоения новых знаний Этапы урока: - организационный - этап проверки домашнего задания - актуализация знаний учащихся - объяснение ...Соотношения между сторонами угла прямоугольного треугольника
─ Ввести понятие синуса, косинуса, тангенса, котангенса, секанса, косеканса острого угла прямоугольного треугольника. ─Научиться решать прямоугольные ...Синус, косинус, тангенс угла
Найти: 1 вариант 2 вариант sin A cos B. sin 30º = cos 60º =. Единичная полуокружность. Определение. Полуокружность называется единичной, если ее ...Свойство углов треугольника
Виды треугольников. B A C E F D N M K Остроугольный Прямоугольный Тупоугольный. Верно ли, что:. - остроугольный треугольник – это треугольник у которого ...Свойство скрещивающихся рёбер правильной треугольной пирамиды
B A C D О. В правильной треугольной пирамиде DABC. №260. через боковое ребро DС и высоту DO пирамиды. проведена плоскость α. М. Докажите, что ребро ...Величина двугранного угла
?. ПОВТОРЕНИЕ ( устная работа). 1) Что называется углом на плоскости? 2) Какой угол называется углом между прямыми в пространстве? 3) Какой угол называется ...Биссектриса угла
Цели:. Повторить с учащимися определение смежных углов, вертикальных углов, теорему о смежных углах, вертикальных углах. Ввести определение биссектрисы, ...Косинус угла
О В А С D. М N C. . Треугольник АВС – прямоугольный. ∟С – прямой. ∟А – острый. АС - прилежащий катет. ВС – противолежащий катет. АВ – гипотенуза. ...Косинус острого угла прямоугольного треугольника
Историческая справка. Расположение углов и сторон. А С В b c a. АС – противолежащий катет. ВС – прилежащий катет. ВС - противолежащий катет. АС – ...Знаменитые задачи древности. Трисекция угла
Выполнил: ученик 6 класса Зеленин Никита Руководитель: учитель математики Левищенко О. П. Образовательное учреждение: МОУ «Средняя общеобразовательная ...Задача о трисекции угла
Задача о трисекции угла разрешима при некоторых частных значениях величины данного угла. A C N M B D. При помощи циркуля и линейки можно разделить ...Зависимость между синусом, косинусом и тангенсом одного и того же угла
∙. . . П р о в е р ь и о ц е н и с е б я ! Ордината Абсцисса. О с н о в н о е т р и г о н о м е т р и ч е с к о е т о ж д е с т в о :. a2-b2=(a-b) ...Геометрия в звездном небе. Свойство углов треугольника
Правила для членов клуба «ПИФАГОР»: Активно знакомиться с геометрическими терминами. 2. Радостно узнавать геометрические фигуры в повседневной жизни. ...Трисекция угла
Цели: познакомиться с историей развития решения задачи деления угла на три равные части; поиск решения задачи наиболее удобным способом; сконструировать ...Угол поворота. Радианная мера угла
Проверка домашней работы. Устный счет. Найдите градусную меру угла. π 2π 450 900 180 1800 3600. Найдите радианную меру угла. 900 1800 3600 180. 2π ...Медианы, биссектрисы и высоты треугольника
Проверка д/з. AH a A a; H a AH – перпендикуляр, проведенный из точки А к прямой а. Н – основание перпендикуляра. Теорема:. Из точки, не лежащей ...Свойство и признак описанного четырёхугольника
3 1 4 5 6 7. Теорема 9.8. В описанном четырёхугольнике суммы противолежащих сторон равны. AB + CD AD + BC ( AK + KB ) CM MD AN ND BL LC =. По свойству ...Конспекты
Черчение прямого угла по угольнику
Государственное казённое специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья. ...Соотношения между тригонометрическими функциями одного и того же угла
Учитель: Уркумбаева Г.М. Класс:9. Тема: «Соотношения между тригонометрическими функциями одного и того же угла». . «Спорт становится средством ...Тригонометрические функции острого угла
МКОУ СОШ с.п.Кара-Суу Черекского района КБР. Айшаева Фердаус Сулеймановна. . "Тригонометрические функции острого угла" Геометрия 8 класс. ...Синус, косинус и тангенс угла
Разработка урока в 9 классе «Синус, косинус, и тангенс угла». Предмет. : Геометрия. Класс. :9 класс. Авторы учебника. : Атанасян Л.С., Бутузов ...Синус, косинус и тангенс угла
Николаева Н.С. . . Тематическая разработка урока. курса «Геометрия» в 9 классе. Учитель: Николаева Наталья Сергеевна. Учебник:. «Геометрия» ...Свойство сложения чисел
Урок математики в 1 классе. ГОУ СОШ № 316 г. Санкт-Петербург. По учебнику. «Математика» 2 класс С.С. Минаева, Л.О.Рослова, О.А. Рыдзе. Тема: ...Свойство упорядоченности и бесконечности числового ряда
. Муниципальное бюджетное общеобразовательное учреждение. Средняя общеобразовательная школа № 3. . Конспект урока по математике. «Свойство ...Свойство деления числа на произведение
Муниципальное общеобразовательное учреждение. «Северная средняя общеобразовательная школа№1. Белгородского района Белгородской области". ...Свойство противоположных сторон прямоугольника
Математика, 2 класс. . тема "Свойство противоположных сторон прямоугольника". . . Вид: изучение и первичное закрепление новых знаний. Тип: ...Свойство вычитания
Технологическая карта изучения темы «. Свойство вычитания». . . Тип урока:. ОНЗ (технология деятельностного метода). Урок составлен к учебнику ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 мая 2019
Категория:Математика
Классы:
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию