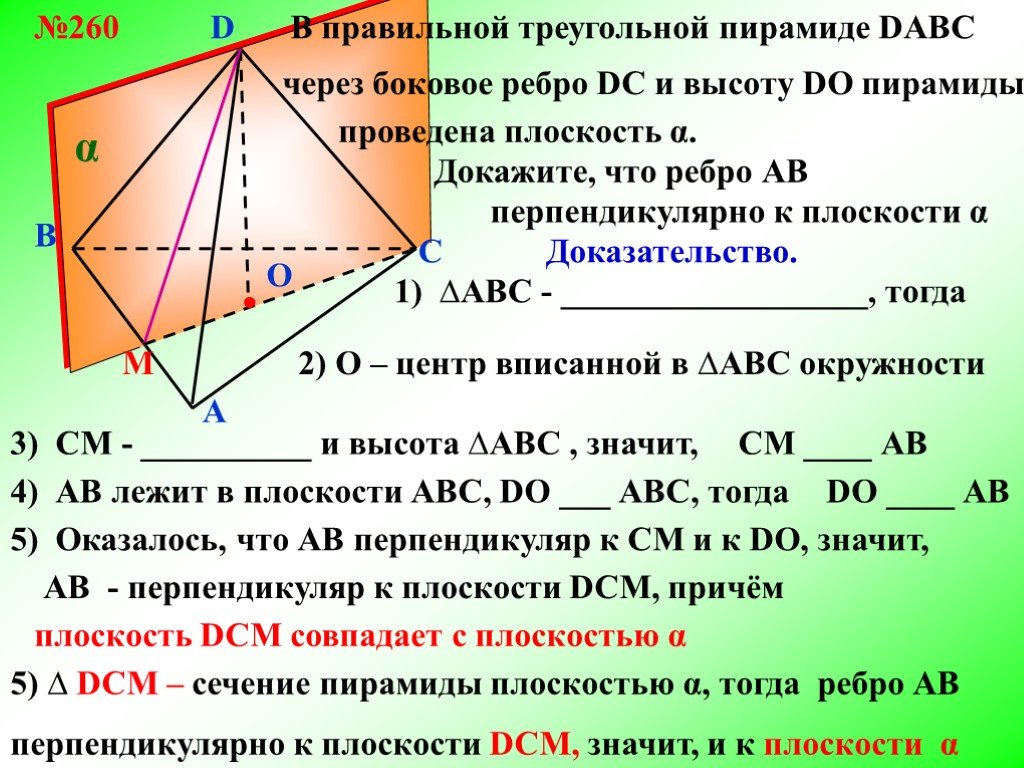
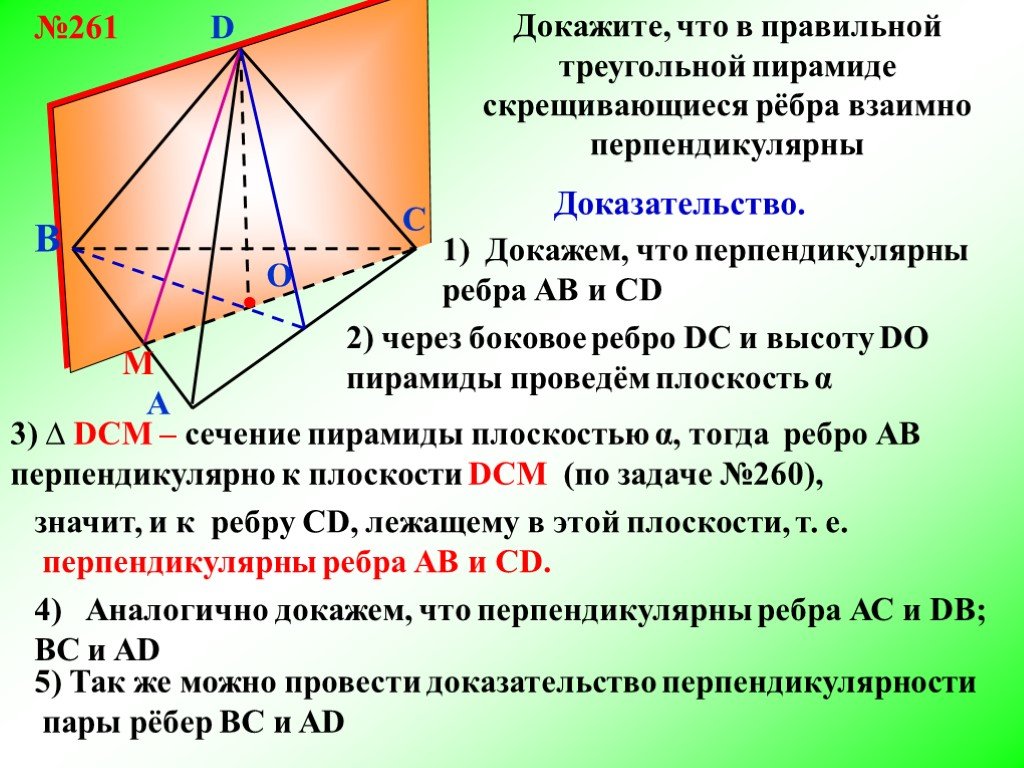
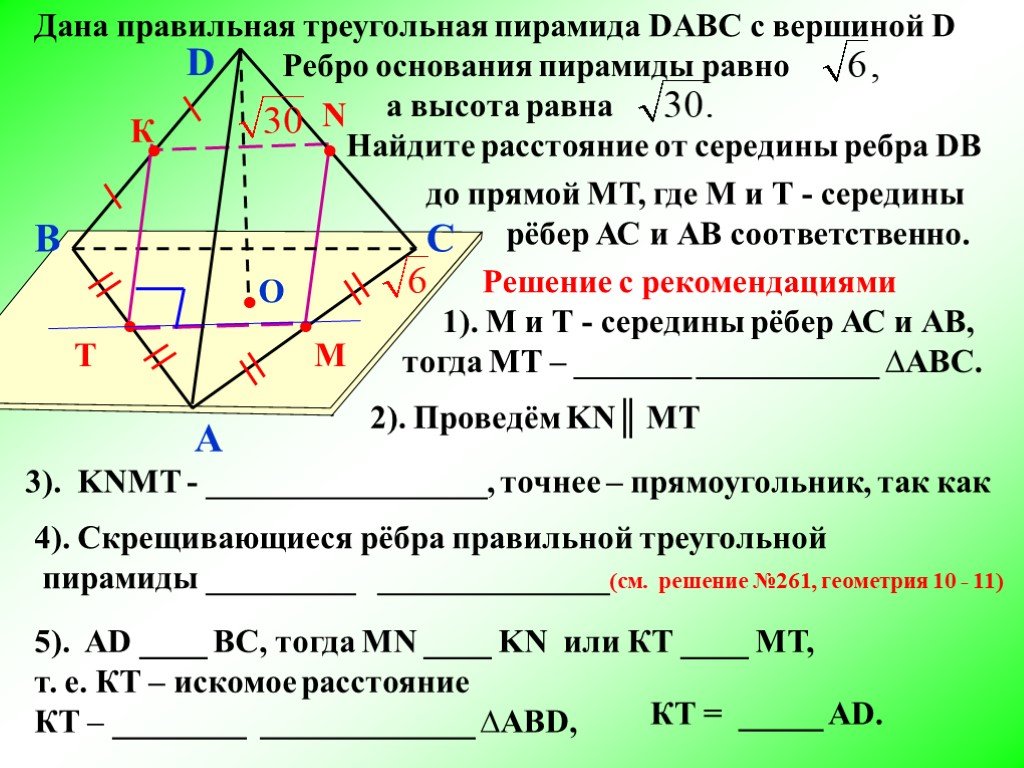
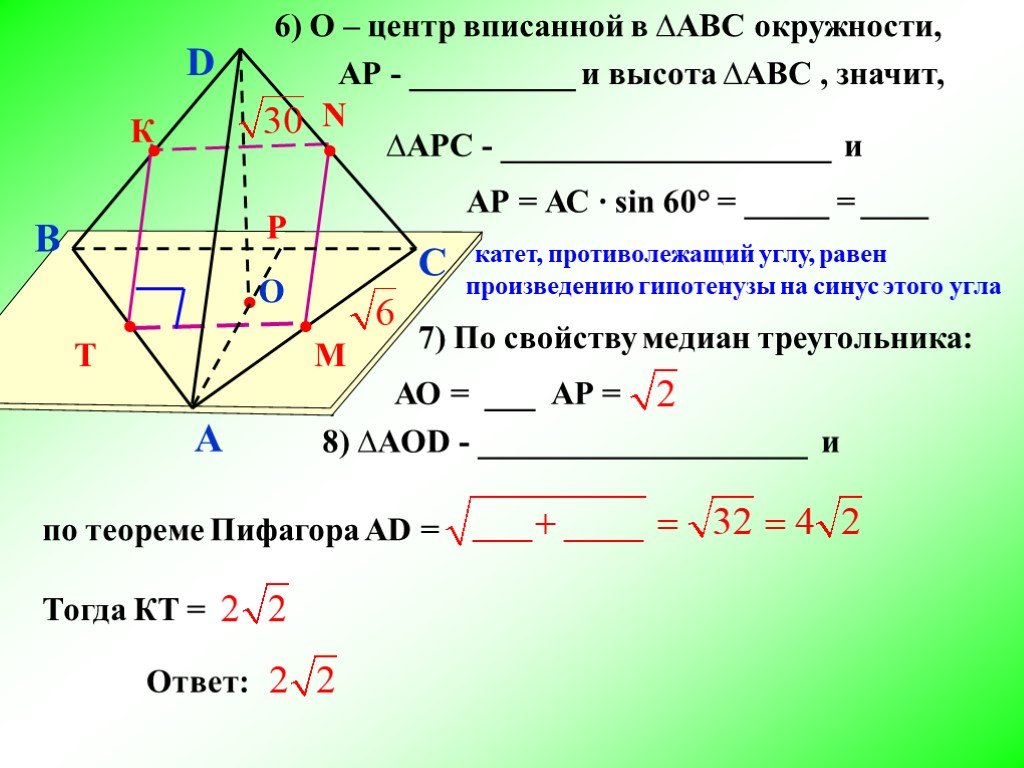
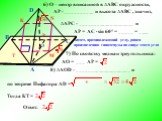
Презентация "Свойство скрещивающихся рёбер правильной треугольной пирамиды" по математике – проект, доклад
Презентацию на тему "Свойство скрещивающихся рёбер правильной треугольной пирамиды" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 7 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойство биссектрисы угла
Цели урока:.Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Учить применять данные теоремы и следствие при решении задач. Формировать ...
Свойство биссектрисы
Цели урока:.Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Учить применять данные теоремы и следствие при решении задач. Исторически ...
Свойство биссектрисы равнобедренного треугольника
Повторение. Треугольник, у которого 2 стороны равны, называется равнобедренным треугольником. D С E B A C H M. DM – медиана треугольника АDВ. AM = ...Сечения пирамиды
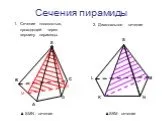
3. Сечение пирамиды плоскостью с заданным следом. A B C F P Q MNPQ - сечение. 4. Сечение пирамиды плоскостью, параллельной основанию. MNKP - сечение ...Египетские пирамиды
Почему Египетские пирамиды называют немым трактатом по геометрии? Автор: Зеленцов Роман 10а класс. МОУ СОШ с.Становое. 2008 год. Цель: научиться определять ...Свойство описанного четырехугольника
Тест. Тема «Свойство описанного четырехугольника». Теорема: В любом описанном четырехугольнике суммы противоположных сторон равны. Дано: ABCD-описанный ...Свойство точек биссектрисы угла
Основополагающий вопрос. - Как расположены точки биссектрисы угла от его сторон? - Какой фигурой будет геометрическое место точек, равноудалённых ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Пирамида. Сечения пирамиды
. Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD. Построить линейный угол двугранного угла, образованного плоскостью ...Объем пирамиды
Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Объем пирамиды
Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...Загадка пирамиды
I Вступление II. Из истории. 1. Пирамида Джосера 2. Пирамида Хеопса III. Об Александре Голоде IV. Пирамида и архитектура 1. Исследования и практическое ...Свойство и признак описанного четырёхугольника
3 1 4 5 6 7. Теорема 9.8. В описанном четырёхугольнике суммы противолежащих сторон равны. AB + CD AD + BC ( AK + KB ) CM MD AN ND BL LC =. По свойству ...Понятие пирамиды
Маршрут путешествия. Египет- страна Пирамид Пирамиды на Марсе Пирамиды в химии Пирамиды в экономике Пирамиды в геометрии. Путешествие вокруг света. ...Свойство корней в степени n
Заполните пропуски. Он есть у дерева, цветка, Он есть у уравнений. И знак особый - √ - ……. С ним связан, вне сомнений. Заданий многих он итог, И с ...Построение пирамиды в зависимости от положения высоты
Две боковые грани перпендикулярны плоскости основания. Высота пирамиды проходит через вершину основания и является минимальным боковым ребром пирамиды. ...Свойство периодичности
Периодические функции. В природе и технике часто встречаются явления, повторяющиеся по истечении некоторого промежутка времени. Например, при вращении ...Решение задач на комбинации призмы, шара и пирамиды
Шар, вписанный в пирамиду. В любую треугольную пирамиду можно вписать шар; В пирамиду, у которой в основание можно вписать окружность; центр, которой ...Конспекты
Свойство сложения чисел
Урок математики в 1 классе. ГОУ СОШ № 316 г. Санкт-Петербург. По учебнику. «Математика» 2 класс С.С. Минаева, Л.О.Рослова, О.А. Рыдзе. Тема: ...Свойство упорядоченности и бесконечности числового ряда
. Муниципальное бюджетное общеобразовательное учреждение. Средняя общеобразовательная школа № 3. . Конспект урока по математике. «Свойство ...Свойство деления числа на произведение
Муниципальное общеобразовательное учреждение. «Северная средняя общеобразовательная школа№1. Белгородского района Белгородской области". ...Свойство противоположных сторон прямоугольника
Математика, 2 класс. . тема "Свойство противоположных сторон прямоугольника". . . Вид: изучение и первичное закрепление новых знаний. Тип: ...Свойство вычитания
Технологическая карта изучения темы «. Свойство вычитания». . . Тип урока:. ОНЗ (технология деятельностного метода). Урок составлен к учебнику ...Проецирование вершин, рёбер и граней
Четверик Ольга Николаевна учитель технологии. . 1 квалификационной категориип. Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательнаяшкола ...Проекция вершины пирамиды на плоскость основания
Метод проектов. . Проекция вершины пирамиды на плоскость основания. Тип:. исследовательский. Учебный предмет:. геометрия. Участники:. 10 класс. ...Площади поверхностей призмы, пирамиды, усеченной пирамиды
Тема урока: «. Площади поверхностей призмы, пирамиды, усеченной пирамиды. ». . Цели и задачи урока. Учебная цель –. закрепить и систематизировать ...Объем пирамиды
Коспект урока по геометрии в 11 классе «Объем пирамиды». Цели занятия:. 1. . Образовательные:. • ознакомление учащихся с геометрическим телом – ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:2 октября 2019
Категория:Математика
Содержит:7 слайд(ов)
Поделись с друзьями:
Скачать презентацию