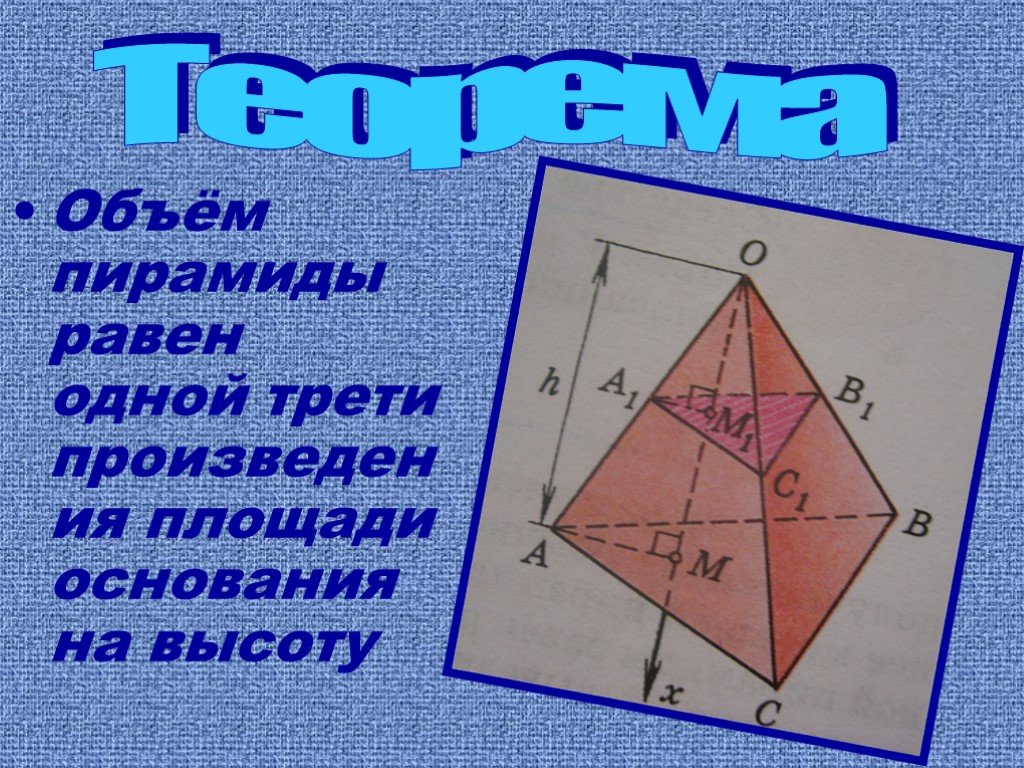
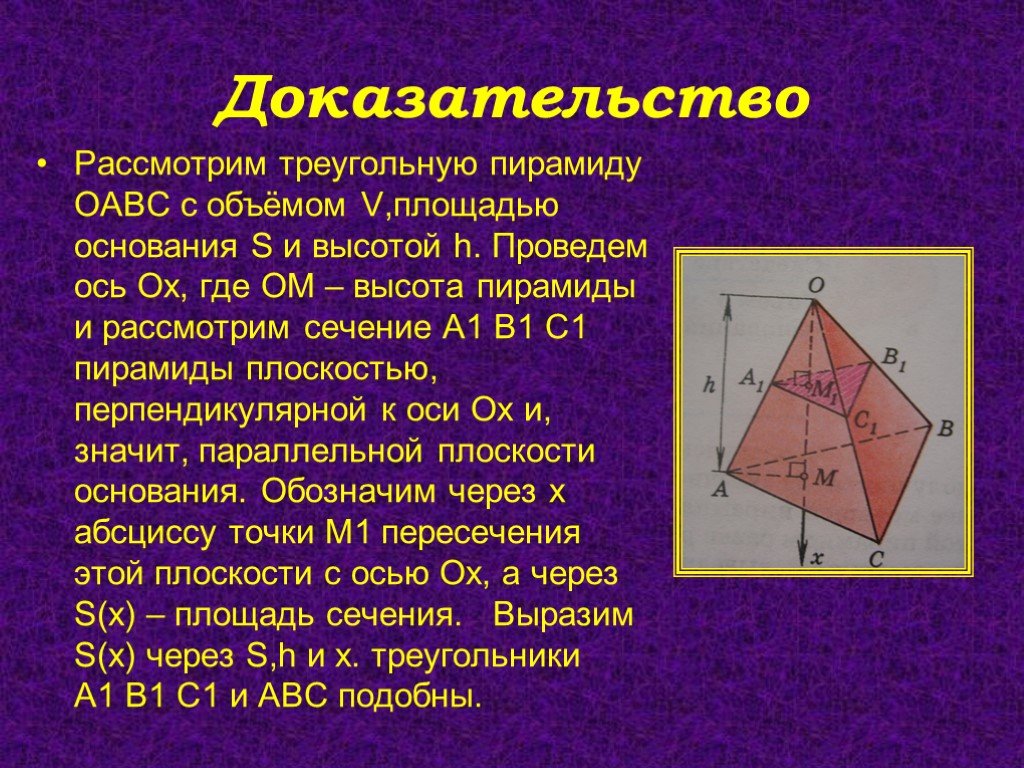
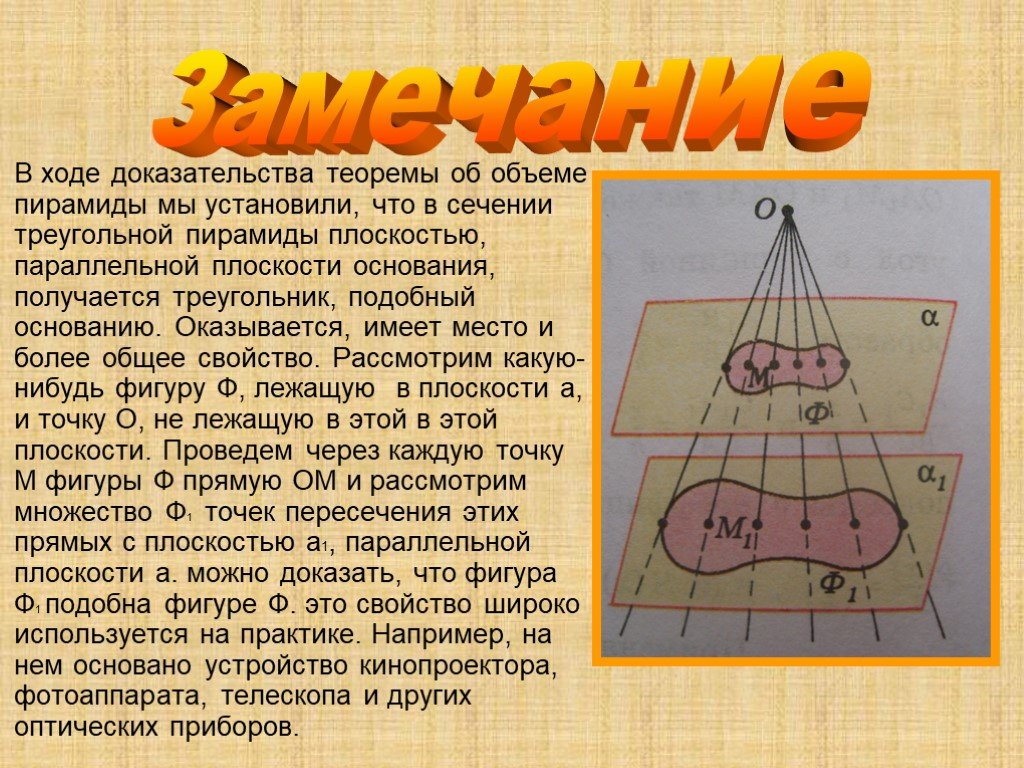
Презентация "Объём пирамиды" по математике – проект, доклад
Презентацию на тему "Объём пирамиды" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Загадка пирамиды
I Вступление II. Из истории. 1. Пирамида Джосера 2. Пирамида Хеопса III. Об Александре Голоде IV. Пирамида и архитектура 1. Исследования и практическое ...Свойства пирамиды с равными боковыми ребрами
Теорема 1.1. Дано: МАВС - треугольная пирамида, МО – высота пирамиды, боковые ребра равны АМ=ВМ=СМ. Доказать: АО = ВО = СО. Теорема 1.2. Дано: МАВС ...Сечения пирамиды
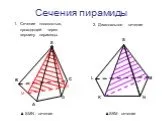
3. Сечение пирамиды плоскостью с заданным следом. A B C F P Q MNPQ - сечение. 4. Сечение пирамиды плоскостью, параллельной основанию. MNKP - сечение ...Площадь. Объём
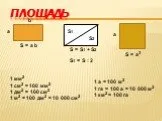
Объем. Вершины, ребра, грани. Прямоугольный параллелепипед V = a b c. Куб V = a3 c. 1 мм3 1 см3 = 1 000 мм3 1 дм3 = 1 л = 1 000 см3 1 м3 = 1 000 дм3 ...Построение пирамиды в зависимости от положения высоты
Две боковые грани перпендикулярны плоскости основания. Высота пирамиды проходит через вершину основания и является минимальным боковым ребром пирамиды. ...Объём шара и площадь сферы
План:. Понятия: Сфера Круговой сектор Шар Шаровой сегмент Шаровой слой Шаровой сектор Формула для вычисления площади сферы Формулы для вычисления ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Объем пирамиды
Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...Объём призмы
ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ: I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы. Объем каждого тела выражается положительным ...Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Объем пирамиды
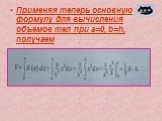
Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...Объём многогранника
Многогранник. Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, ...Объём конуса
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна ...Объём и содержание понятия
Дайте характеристику следующим объектам. Форма, цвет, размер. Охарактеризуйте объект. СОДЕРЖАНИЕ ПОНЯТИЯ. это все существенные признаки объекта или ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объём прямоугольного параллелепипеда
. «Дорогой Хагрид! Оставляю под Вашим присмотром этого дракончика, для которого срочно придётся приобрести аквариум, так как на суше его можно держать ...Объём шара и его частей
Объём шара. Объём шара радиуса R равен. Шаровой сегмент. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровой ...Объём прямоугольного параллелепипеда
Блиц-Опрос. Прямоугольный параллелепипед – это (плоская, объёмная) фигура. Стороны граней параллелепипеда называются _______________. У параллелепипеда ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Объём тел
Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем систему координат – ось ох перпендикулярна ...Конспекты
Площади поверхностей призмы, пирамиды, усеченной пирамиды
Тема урока: «. Площади поверхностей призмы, пирамиды, усеченной пирамиды. ». . Цели и задачи урока. Учебная цель –. закрепить и систематизировать ...Проекция вершины пирамиды на плоскость основания
Метод проектов. . Проекция вершины пирамиды на плоскость основания. Тип:. исследовательский. Учебный предмет:. геометрия. Участники:. 10 класс. ...Объём прямоугольного параллелепипеда
Предмет:. математика. Класс:. 5. Учитель. : Булатова Анна Васильевна. Базовый учебник:. Муравин Г. К., Муравина О. В. «Математика»,5 класс. ...Объёмы. Объём прямоугольного параллелепипеда
Урок математики в 5 классе. Подклетнева И.В.( МОБУ Гимназия №15 г. Сочи),Боклаг В.Н. (МОБУ СОШ №10 г. Сочи). . Урок математики в 5 классе. Подклетнева ...Объём прямоугольного параллелепипеда
МБОУ Белоберезковская СОШ №1 Трубчевского района Брянской области. Урок по теме «Объём прямоугольного параллелепипеда». 5-й класс. Ананченко ...Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипеда. Цель:. Обобщить, повторить и систематизировать знания по теме: «Объём. Объем прямоугольного параллелепипеда». ...Объём прямоугольного паралле-лепипеда
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2 с.Октябрьское». МО – Пригородный район РСО - Алания. ...Объем пирамиды
Коспект урока по геометрии в 11 классе «Объем пирамиды». Цели занятия:. 1. . Образовательные:. • ознакомление учащихся с геометрическим телом – ...Объём многогранников. Решение профессионально значимых задач
Авторская работа на тему:. . «Объём многогранников. Решение профессионально значимых задач». Автор работы:. . преподаватель математики выс. ...Объём куба и прямоугольного параллелепипеда. Кубический см
Ленинская средняя школа. Разработка открытого урока математики в 4 классе на тему:. « Объём куба и прямоугольного ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 июня 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию