Презентация "Объём призмы" по математике – проект, доклад
Презентацию на тему "Объём призмы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
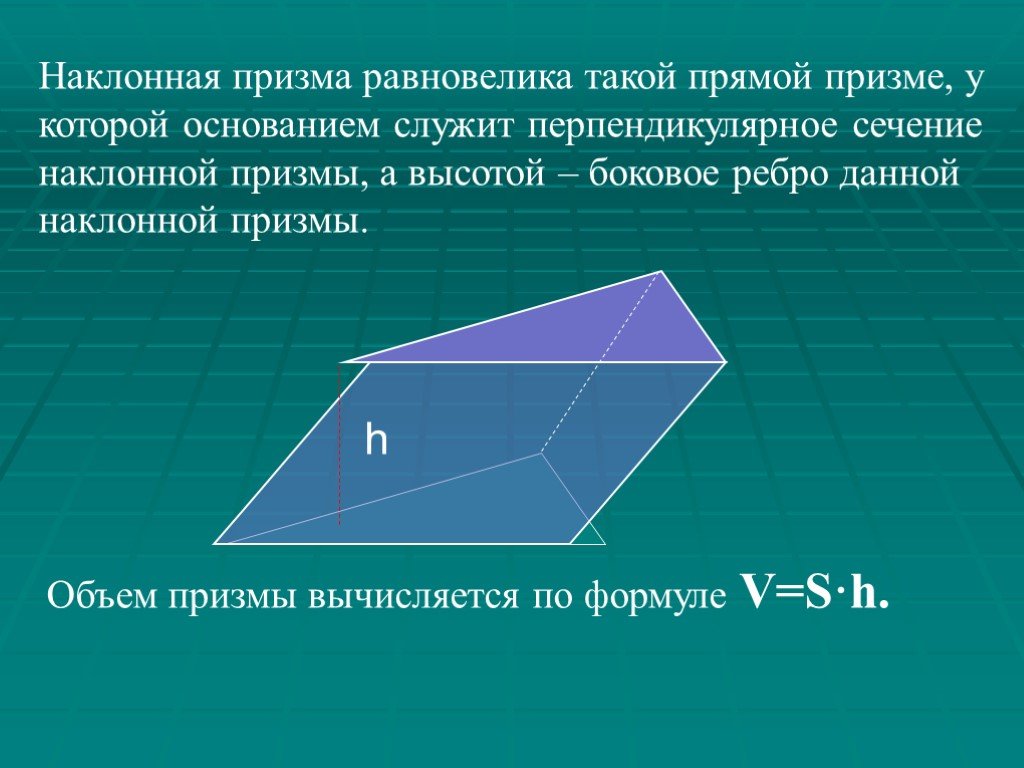
Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Объём цилиндра и конуса
«Не стыдись спросить – не знать еще стыднее!» Японская пословица. В игре участвуют 2 команды. Капитан команды выбирает номер задания, и команда приступает ...Объём конуса
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна ...Свойства призмы
Сколько ребер может иметь выпуклый многогранник? Почему не может быть 7 ребер? Рассмотрим F и не принадлежащую прямой а. XF проведем равные отрезки ...призмы
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой. ...Площадь. Объём
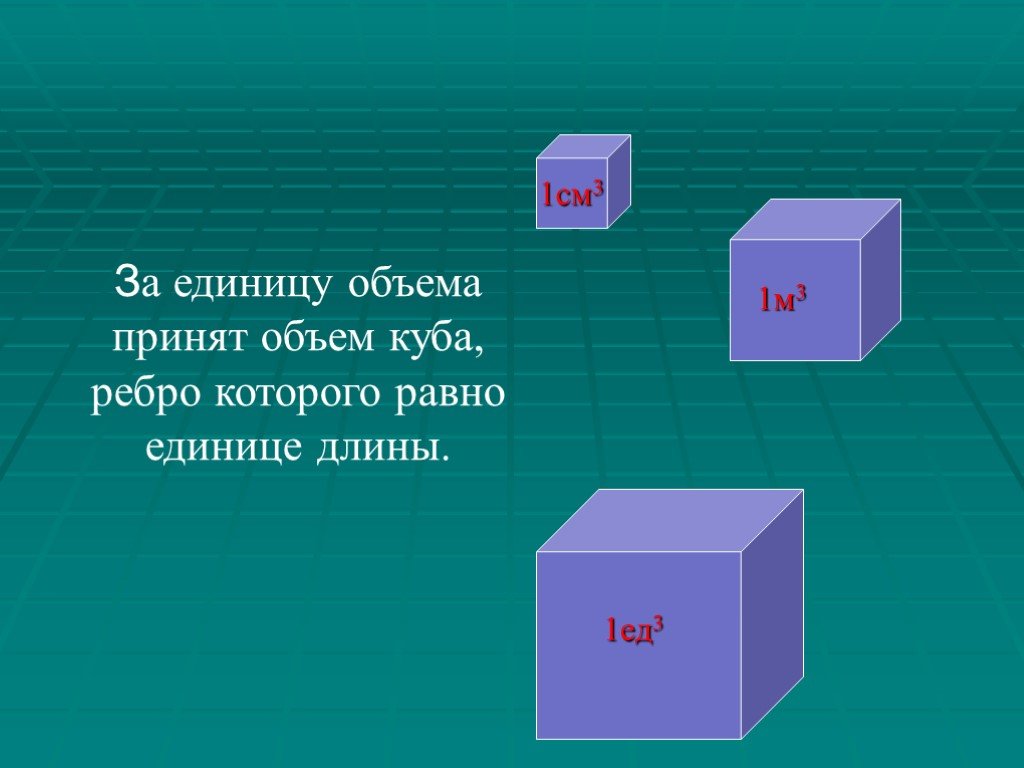
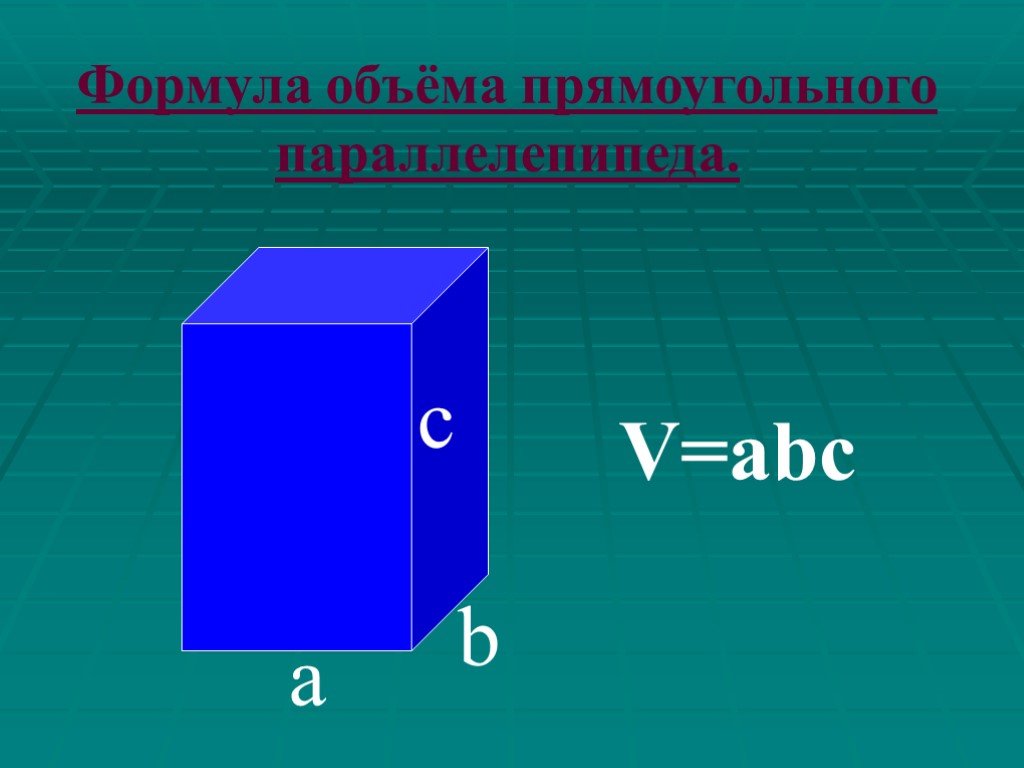
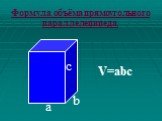
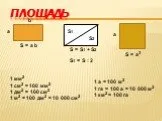
Объем. Вершины, ребра, грани. Прямоугольный параллелепипед V = a b c. Куб V = a3 c. 1 мм3 1 см3 = 1 000 мм3 1 дм3 = 1 л = 1 000 см3 1 м3 = 1 000 дм3 ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Объём шара и площадь сферы
План:. Понятия: Сфера Круговой сектор Шар Шаровой сегмент Шаровой слой Шаровой сектор Формула для вычисления площади сферы Формулы для вычисления ...Объем прямой призмы
Цели урока:. Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике. Призма ...Объем прямой призмы
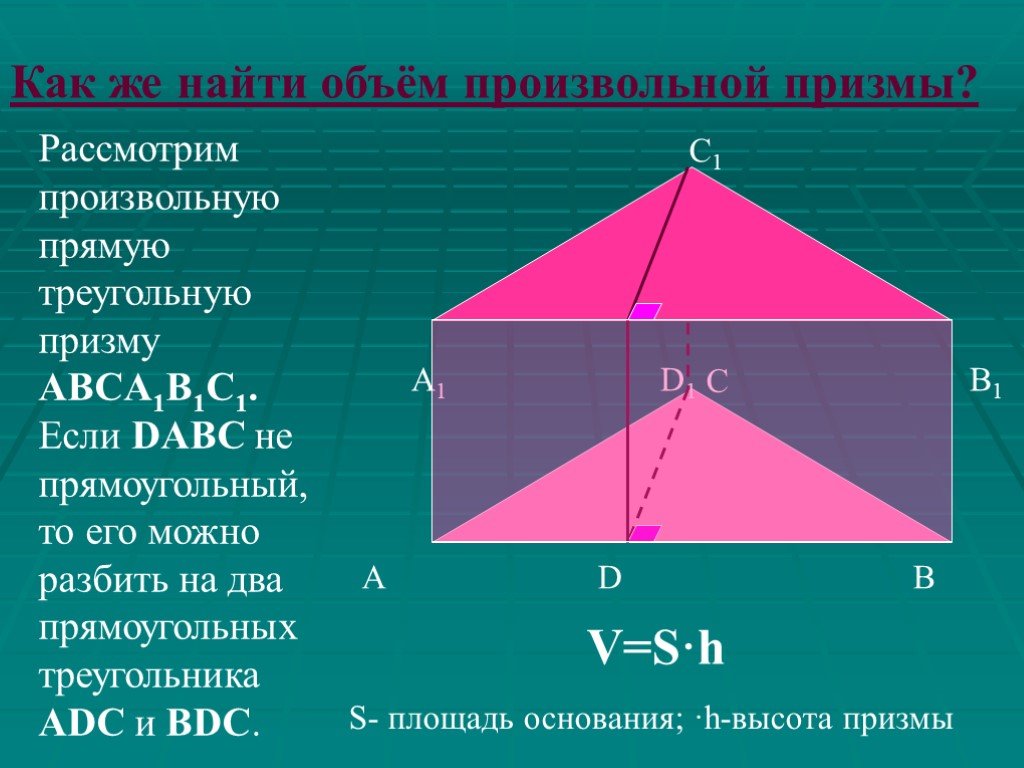
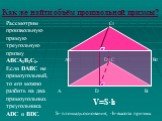
Теорема: объем прямой призмы равен произведению площади основания на высоту. Доказательство. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ ...Объем призмы
Ход урока:. Вступительное слово учителя Повторение материала проводится в форме игры «Поле чудес Правила игры: выбор троек игроков после правильного ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Объём многогранника
Многогранник. Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объём прямоугольного параллелепипеда
. «Дорогой Хагрид! Оставляю под Вашим присмотром этого дракончика, для которого срочно придётся приобрести аквариум, так как на суше его можно держать ...Объём шара и его частей
Объём шара. Объём шара радиуса R равен. Шаровой сегмент. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровой ...Объём прямоугольного параллелепипеда
Блиц-Опрос. Прямоугольный параллелепипед – это (плоская, объёмная) фигура. Стороны граней параллелепипеда называются _______________. У параллелепипеда ...Объемы параллелепипеда и призмы
Цель:. учиться применять формулы объема параллелепипеда и призмы при решении различных задач. План урока. Повторение пройденного материала. Физический ...Объём тел
Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем систему координат – ось ох перпендикулярна ...Площадь поверхности призмы
Основанием треугольной призмы является равнобедренный прямоугольный треугольник. Ровно одна ее грань — квадрат, известны длины ее ребер и высота. ...Конспекты
Площади поверхностей призмы, пирамиды, усеченной пирамиды
Тема урока: «. Площади поверхностей призмы, пирамиды, усеченной пирамиды. ». . Цели и задачи урока. Учебная цель –. закрепить и систематизировать ...Объём прямоугольного параллелепипеда
Предмет:. математика. Класс:. 5. Учитель. : Булатова Анна Васильевна. Базовый учебник:. Муравин Г. К., Муравина О. В. «Математика»,5 класс. ...Объёмы. Объём прямоугольного параллелепипеда
Урок математики в 5 классе. Подклетнева И.В.( МОБУ Гимназия №15 г. Сочи),Боклаг В.Н. (МОБУ СОШ №10 г. Сочи). . Урок математики в 5 классе. Подклетнева ...Объём прямоугольного параллелепипеда
МБОУ Белоберезковская СОШ №1 Трубчевского района Брянской области. Урок по теме «Объём прямоугольного параллелепипеда». 5-й класс. Ананченко ...Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипеда. Цель:. Обобщить, повторить и систематизировать знания по теме: «Объём. Объем прямоугольного параллелепипеда». ...Объём прямоугольного паралле-лепипеда
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2 с.Октябрьское». МО – Пригородный район РСО - Алания. ...Объем наклонного параллелепипеда. Объем призмы
Технологическая карта. Класс – 11. Предмет – геометрия. Тема - Объем наклонного параллелепипеда. Объем призмы. Проверка домашнего задания. ...Объём многогранников. Решение профессионально значимых задач
Авторская работа на тему:. . «Объём многогранников. Решение профессионально значимых задач». Автор работы:. . преподаватель математики выс. ...Объём куба и прямоугольного параллелепипеда. Кубический см
Ленинская средняя школа. Разработка открытого урока математики в 4 классе на тему:. « Объём куба и прямоугольного ...Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда
Конспект урока по математике 4 класс. Тема: «Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда». Подготовила: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 марта 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию