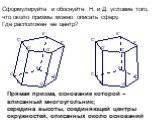
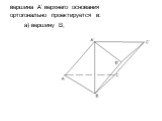
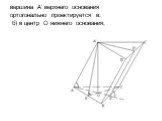
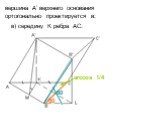
Презентация "Свойства призмы" по математике – проект, доклад
Презентацию на тему "Свойства призмы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства равнобедренного треугольника
Тема: «Свойства равнобедренного треугольника». Геометрия – это искусство хорошо рассуждать ... Нильс Г. Абель. Цели урока:. Создать условия для: введения ...Свойства четырехугольников
Параллелограмм Трапеция Прямоугольник Ромб Квадрат Четырехугольники конец. Параллелограмм -. четырехугольник, у которого противоположные стороны попарно ...Свойства прямоугольного параллелепипеда
Цели:. Определение прямоугольного параллелепипеда Измерения прямоугольного параллелепипеда Формулы для нахождения его квадрата диагонали Формула для ...Свойства функции
Область определения функции. Область определения функции –это множество значений аргумента, при которых функция определена. Область значений функции. ...Свойства функций
Схема исследования:. Область определения Множество значений Нули функции Интервалы знакопостоянства Промежутки монотонности Точки экстремума Набольшее ...Свойства степени с рациональным показателем
Вспомним теорию. Арифметическим корнем n – ой степени (n N, n 2) из неотрицательного числа a называется такое неотрицательное число, n – я степень ...Объем прямой призмы
Теорема: объем прямой призмы равен произведению площади основания на высоту. Доказательство. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ ...Объем прямой призмы
Цели урока:. Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике. Призма ...Объём призмы
ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ: I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы. Объем каждого тела выражается положительным ...Объем призмы
Ход урока:. Вступительное слово учителя Повторение материала проводится в форме игры «Поле чудес Правила игры: выбор троек игроков после правильного ...Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Логарифмы. Свойства логарифма
ЛОГАРИФМЫ. Во многих задачах требуется уметь решать уравнения вида a =b. Для этого надо найти показатель степени по данным значениям степени и её ...Свойства сложения
26 октября. Классная работа. Цель: Знакомство со свойствами сложения (переместительным и сочетательным). Совершенствовать вычислительные навыки и ...Объемы параллелепипеда и призмы
Цель:. учиться применять формулы объема параллелепипеда и призмы при решении различных задач. План урока. Повторение пройденного материала. Физический ...Свойства степеней
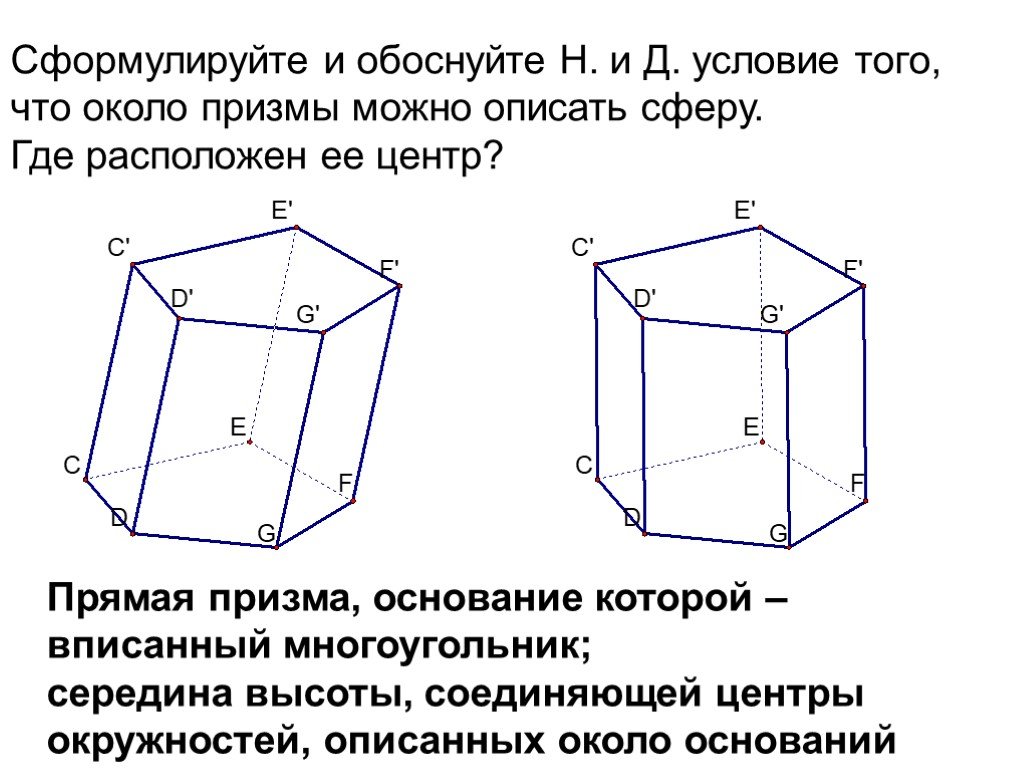
Вычислите, представьте в виде степени или упростите, если возможно. . . . Спасибо за то, что стараешься! ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Свойства степени с натуральным показателем
Квадратные уравнения. 1) х2 + 4x=0 2) х2 – 16 = 0 3) 3x2 + 10 = 0 4) 5x2 = 0 5) 2x2 – 7x = 0. Неполные квадратные уравнения. х2 + 4x=0 , х2 – 16 = ...Параллелограмм. Свойства параллелограмма
Проверка домашнего задания. Параллелограмм – это. четырехугольник равны. многоугольник. у которого противоположные стороны попарно. параллельны. Правильно! ...Конспекты
Свойства степени с целым показателем
Проект урока. Предлагаю вашему вниманию урок алгебры в 8 классе по теме: «Свойства степени с целым показателем». Материал темы расширяет знания учащихся, ...Свойства степени с натуральным показателем
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №7» г. Саянска. Тема урока: Обобщающий урок ...Свойства степени с натуральным показателем
Учитель: Быкова М.Н. Класс:. 7. Тема урока. :. Свойства степени с натуральным показателем. . . Тип урока:. Повторительно-обобщающий урок. ...Свойства сложения и вычитания
УРОК МАТЕМАТИКИ. Учитель:. Голикова А.А. Класс:. 2 «Г». Дата проведения:. 26.01.2010. Тема. Закрепление по теме «Свойства сложения и вычитания». ...Свойства степеней с целыми показателями
02.12.2013. 8-В класс. Урок № 37. Тема урока:. . Решение упражнений и задач по теме «Свойства степеней с целыми показателями». . . Цель урока:. ...Сложение натуральных чисел. Свойства сложения
Конспект. . урока. . разработала. . учитель. . математики. . . . . . Костюкова. . Ольга. . Владимировна. . . Тема урока:. . ...Число 0, цифра 0. Свойства нуля
12.12.08. Математика 1 класс. Петрова О.Н. ТЕМА: Число 0, цифра 0. Свойства нуля. ОСНОВНЫЕ ЦЕЛИ:. Сформировать представление о числе 0 ...Логарифм числа. Свойства логарифмов
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа № 2 р.п Сенной. вольского района саратовской области». . ...Логарифмы. Свойства логарифмов
Филиал боу СПО. «. ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ. ». минздравсоцразвития чувашии Г. КАНАШ чувашской республики. . «. Утверждаю. ». . зав ...Квадратные уравнения. Свойства коэффициентов
Технологическая карта урока математики. Учитель: Раковская Татьяна Ивановна. УМК: Алгебра 8 класс, авторы: Ю.Н. Мордкович, Н.Г. Мюндю, К.И. Пешков, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 сентября 2019
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию



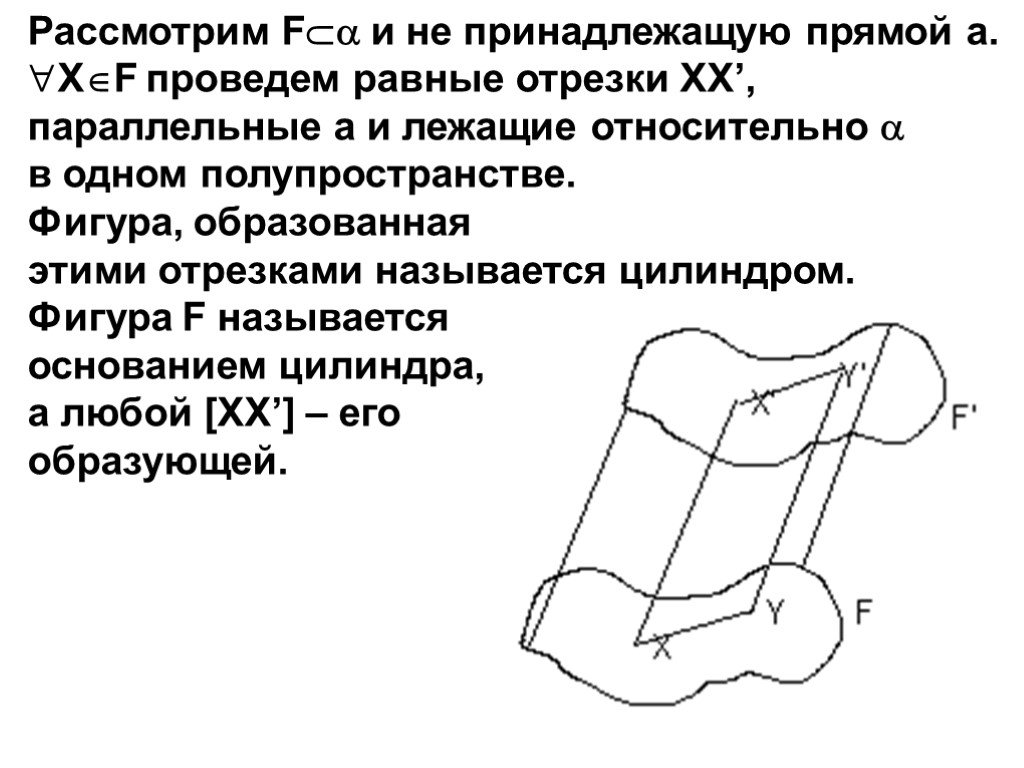
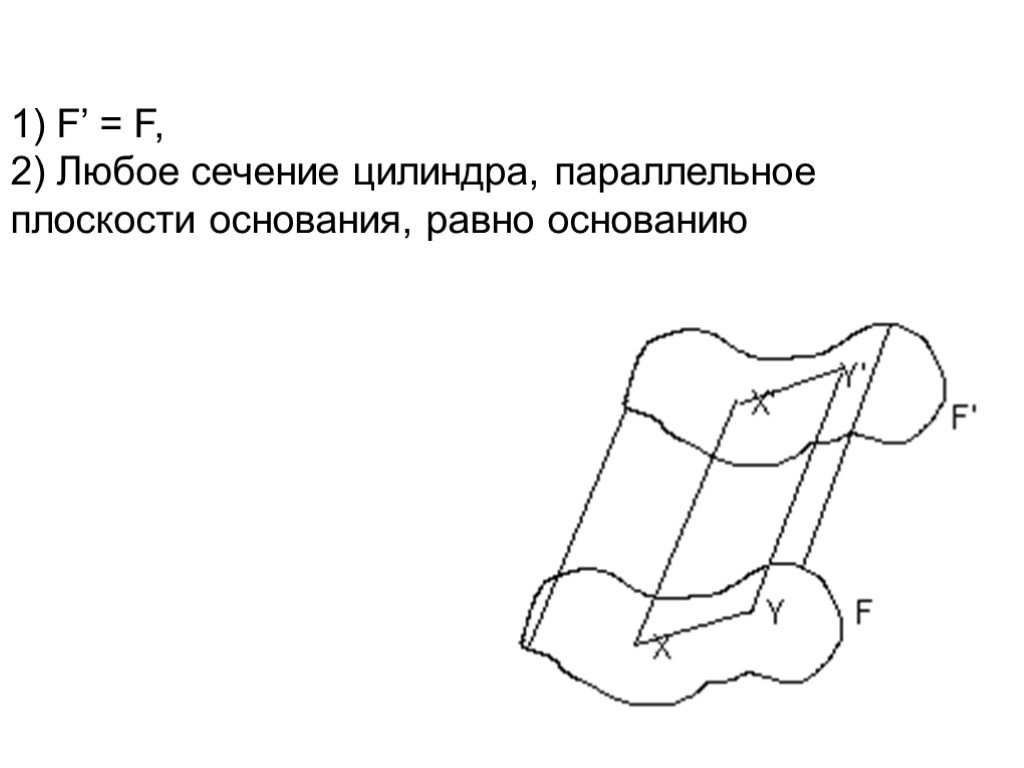





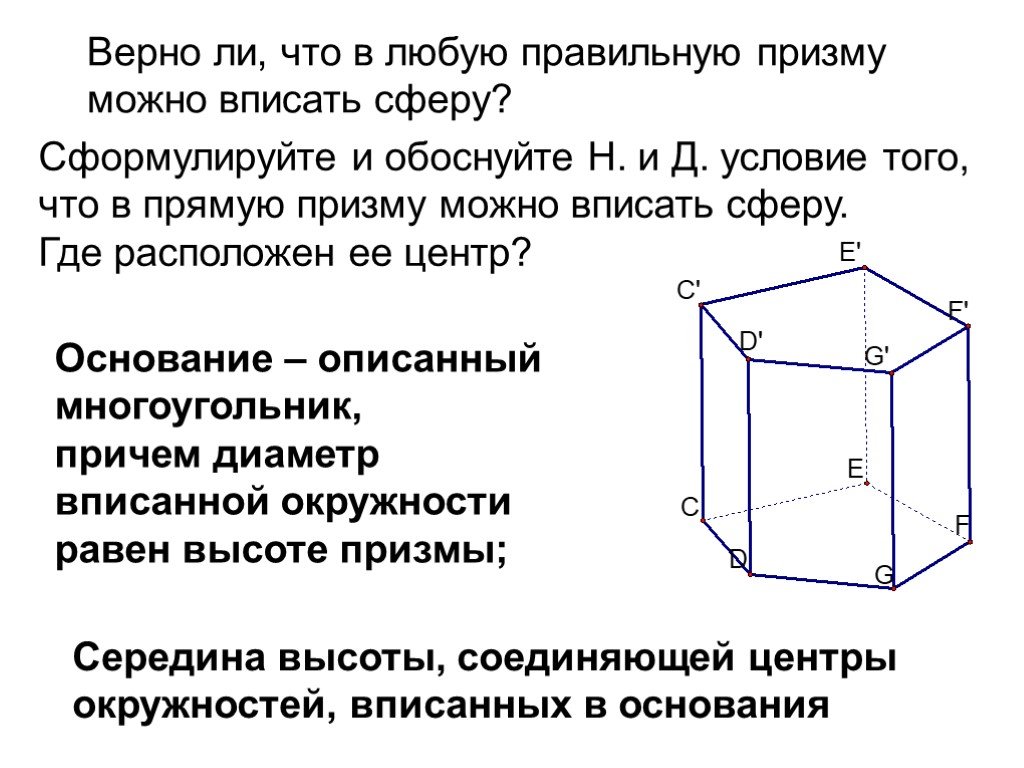

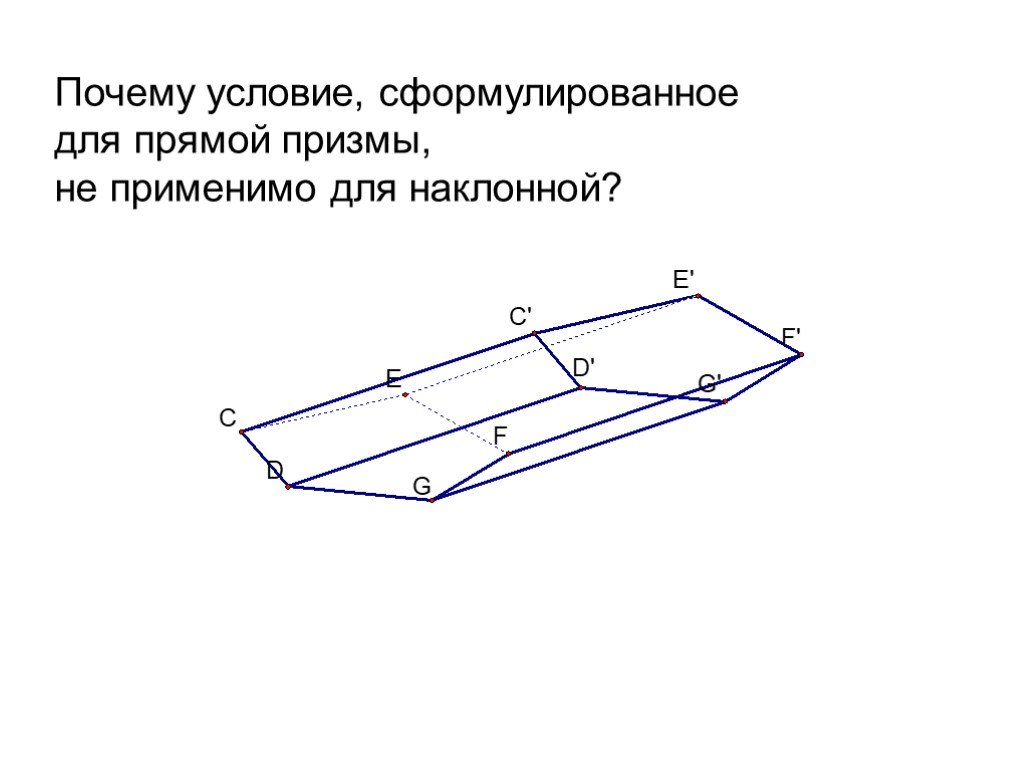


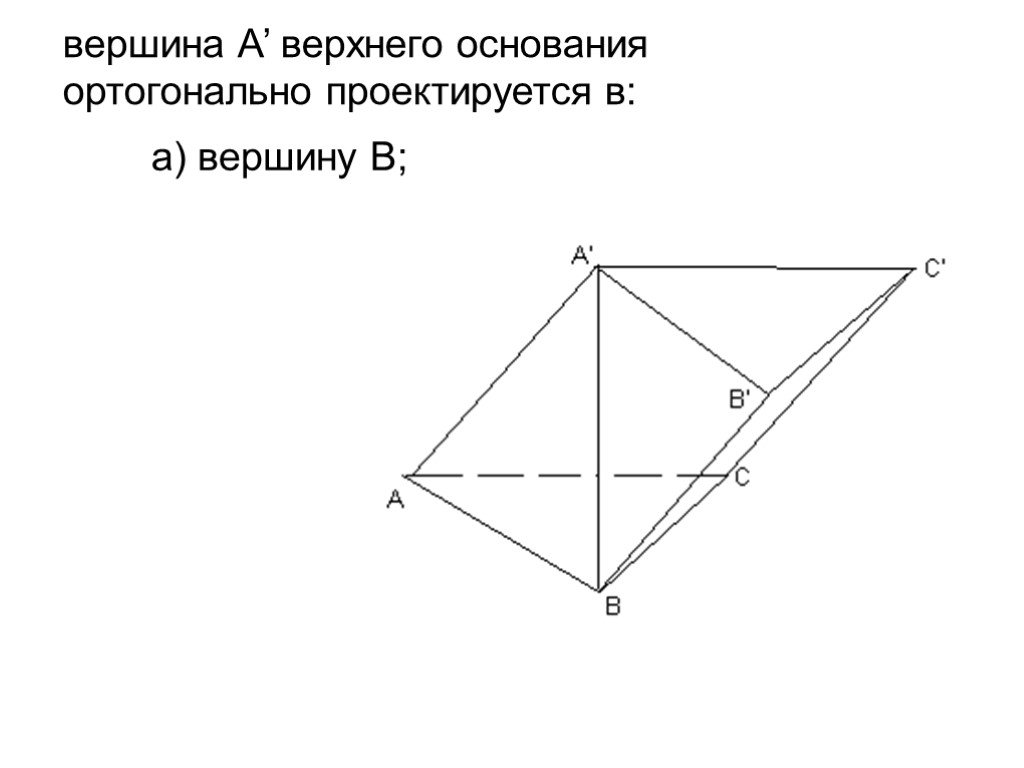
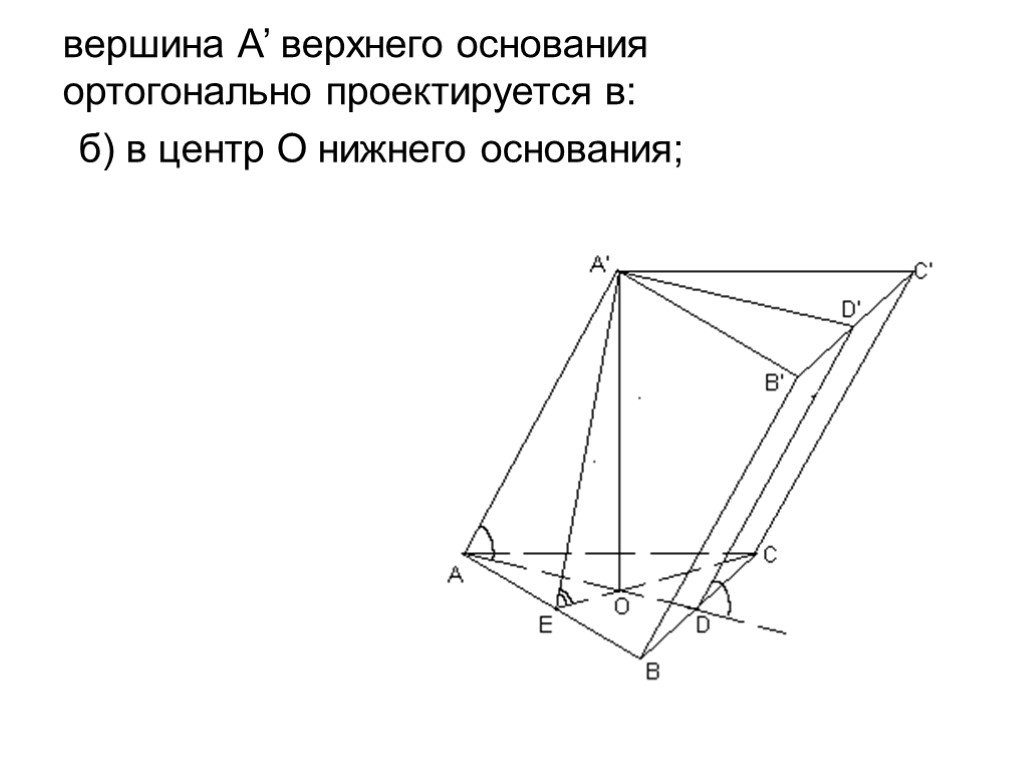
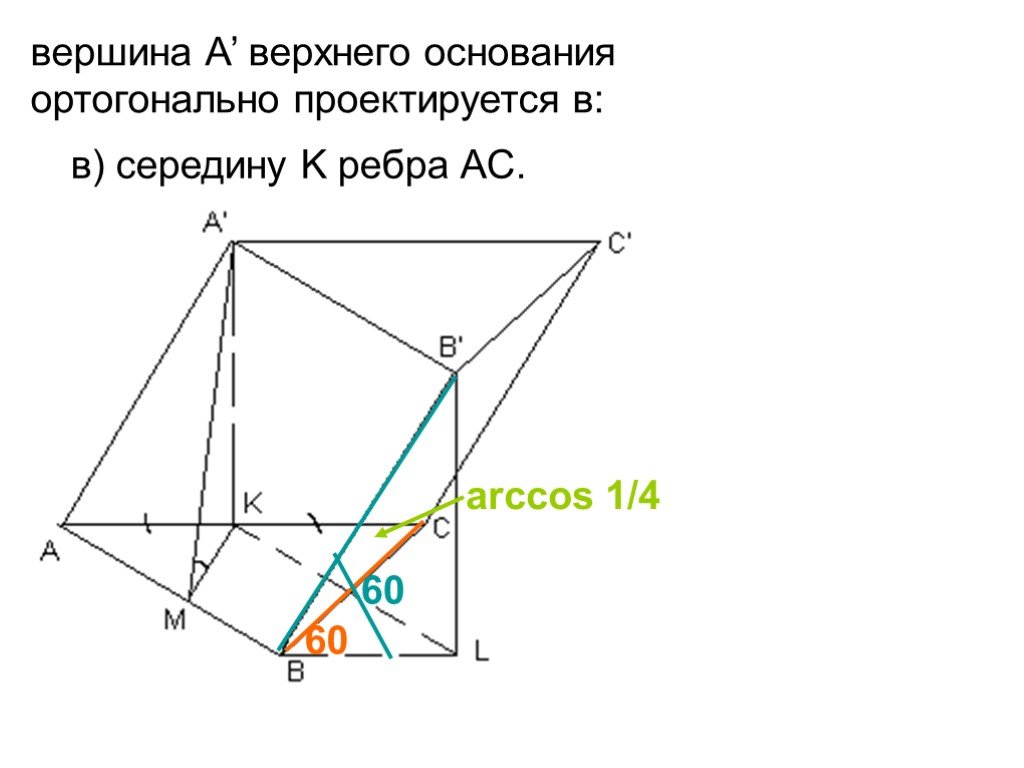
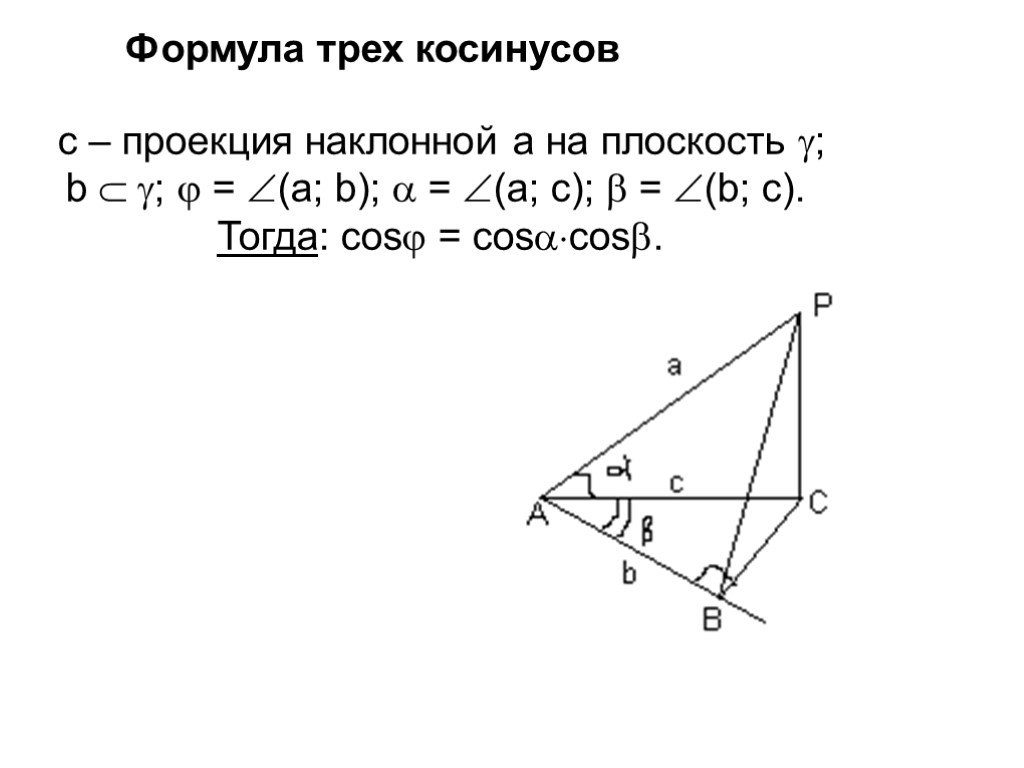
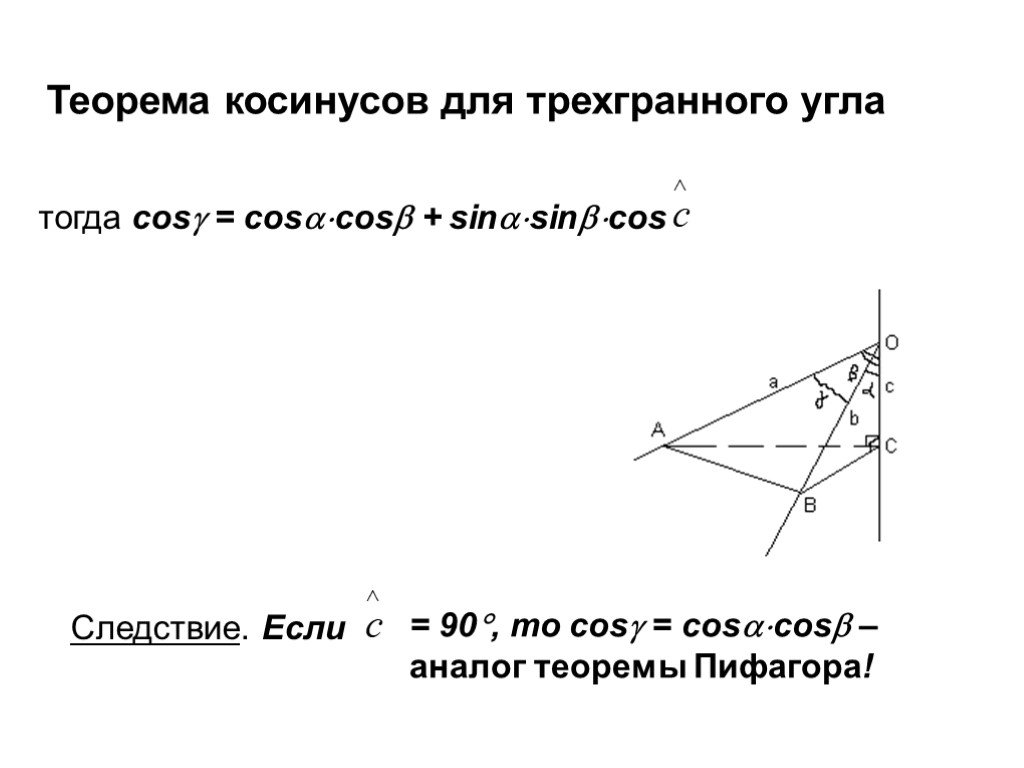



![Рассмотрим F и не принадлежащую прямой а. XF проведем равные отрезки XX’, параллельные а и лежащие относительно в одном полупространстве. Фигура, образованная этими отрезками называется цилиндром. Фигура F называется основанием цилиндра, а любой [XX’] – его образующей. Рассмотрим F и не принадлежащую прямой а. XF проведем равные отрезки XX’, параллельные а и лежащие относительно в одном полупространстве. Фигура, образованная этими отрезками называется цилиндром. Фигура F называется основанием цилиндра, а любой [XX’] – его образующей.](https://prezentacii.org/upload/cloud/19/09/159784/images/thumbs/screen3.jpg)