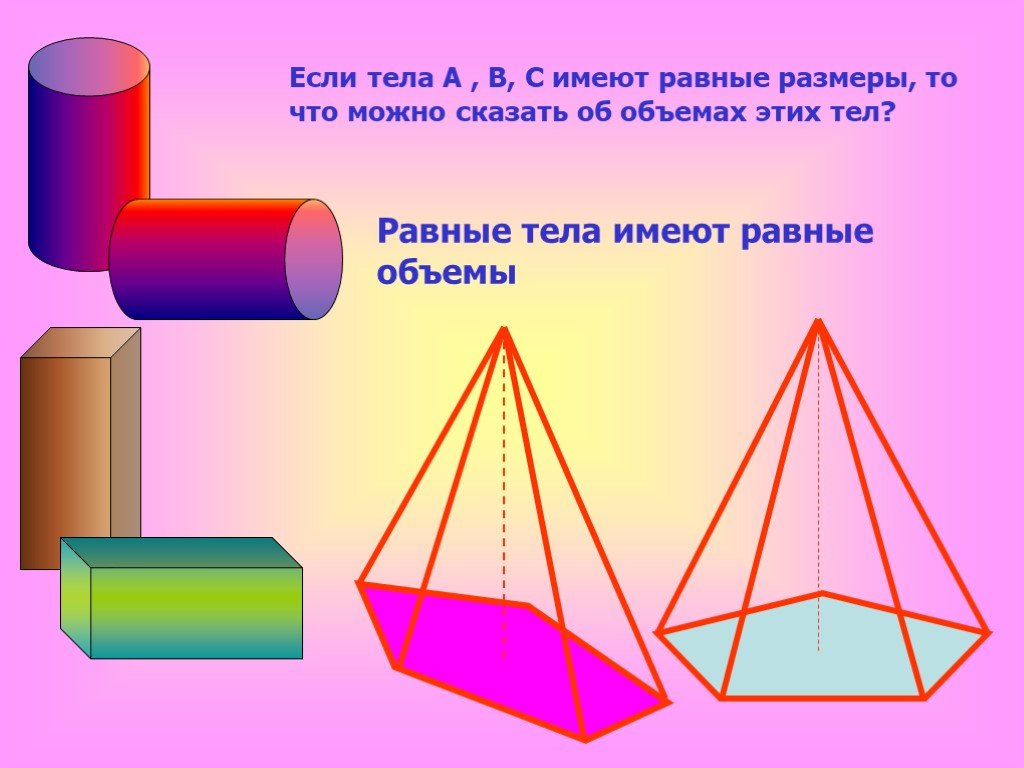
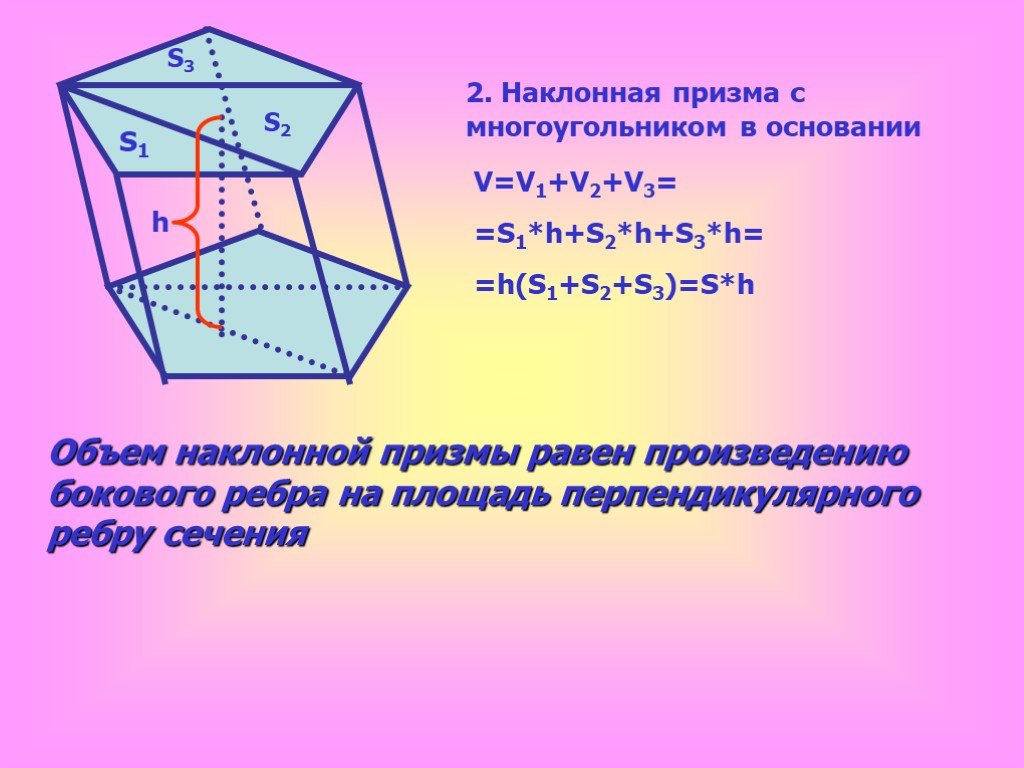
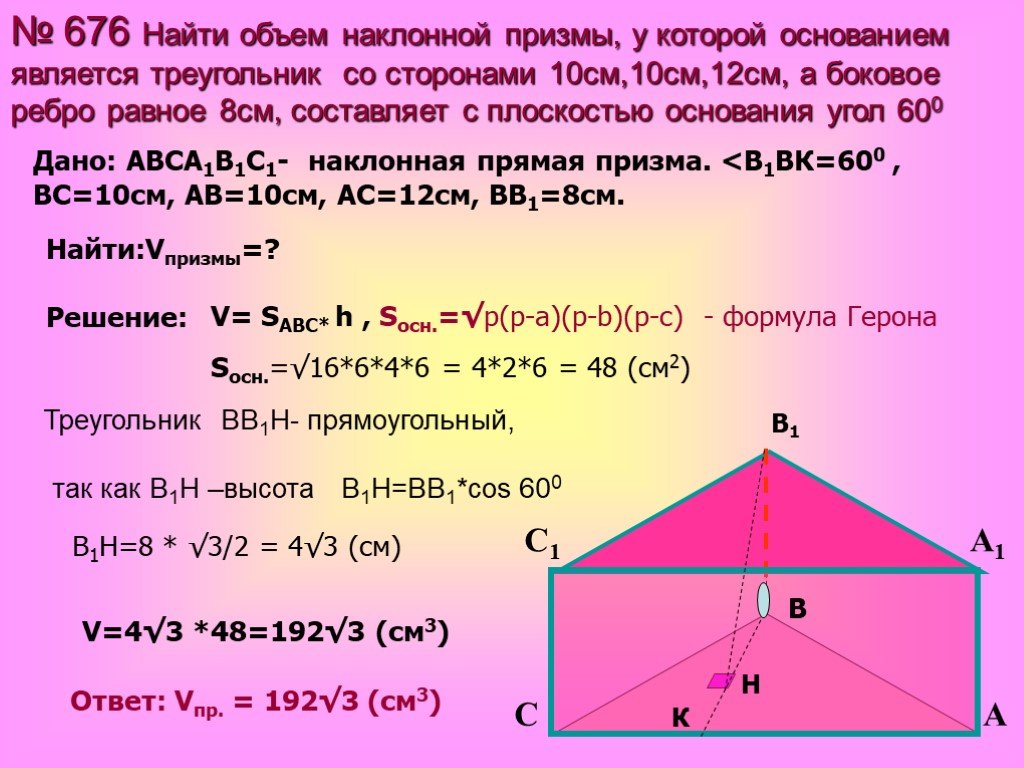
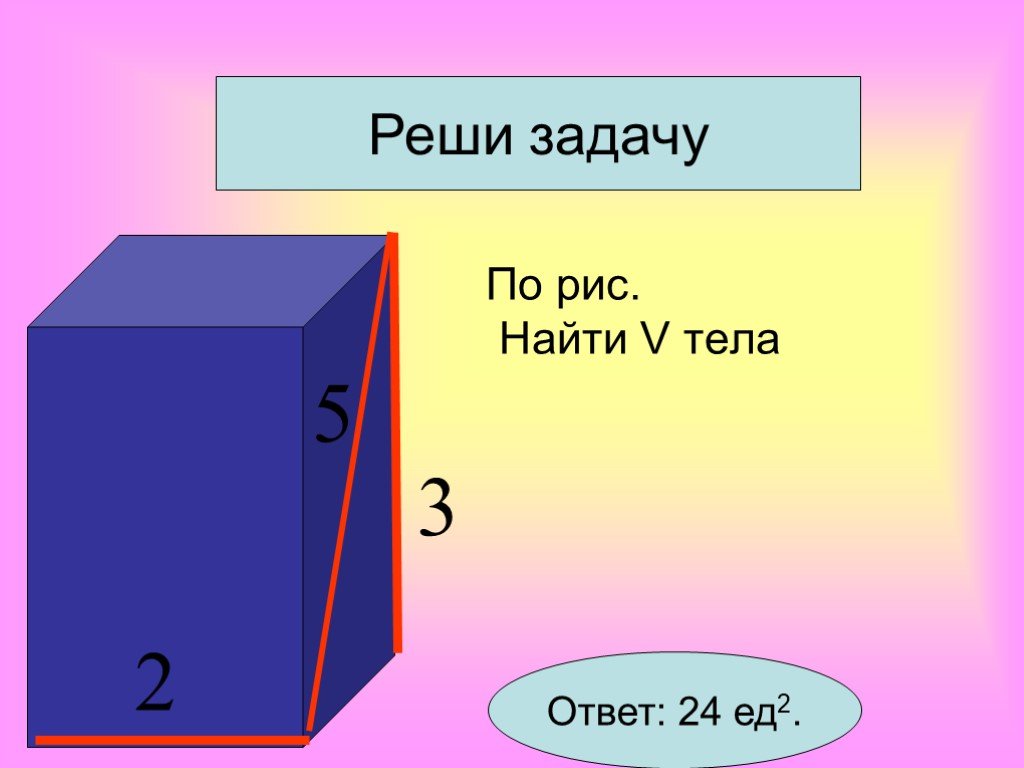
Презентация "Объём наклонной призмы" по математике – проект, доклад
Презентацию на тему "Объём наклонной призмы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Объём призмы
ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ: I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы. Объем каждого тела выражается положительным ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объём конуса
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна ...Свойства призмы
Сколько ребер может иметь выпуклый многогранник? Почему не может быть 7 ребер? Рассмотрим F и не принадлежащую прямой а. XF проведем равные отрезки ...призмы
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой. ...Площадь. Объём
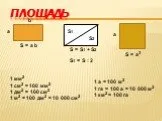
Объем. Вершины, ребра, грани. Прямоугольный параллелепипед V = a b c. Куб V = a3 c. 1 мм3 1 см3 = 1 000 мм3 1 дм3 = 1 л = 1 000 см3 1 м3 = 1 000 дм3 ...Перпендикуляр, наклонная, проекция наклонной на плоскость
отр. АВ- перпендикуляр, проведённый из т. А к плоскости ; т. В- основание перпендикуляра; АВ- расстояние от точки А до плоскости (длина перпендикуляра); ...Объемы параллелепипеда и призмы
Цель:. учиться применять формулы объема параллелепипеда и призмы при решении различных задач. План урока. Повторение пройденного материала. Физический ...Объём прямоугольного параллелепипеда
. «Дорогой Хагрид! Оставляю под Вашим присмотром этого дракончика, для которого срочно придётся приобрести аквариум, так как на суше его можно держать ...Объем прямой призмы
Цели урока:. Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике. Призма ...Объем прямой призмы
Теорема: объем прямой призмы равен произведению площади основания на высоту. Доказательство. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ ...Объем призмы
Ход урока:. Вступительное слово учителя Повторение материала проводится в форме игры «Поле чудес Правила игры: выбор троек игроков после правильного ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Объём многогранника
Многогранник. Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, ...Объём шара и его частей
Объём шара. Объём шара радиуса R равен. Шаровой сегмент. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровой ...Объём прямоугольного параллелепипеда
Блиц-Опрос. Прямоугольный параллелепипед – это (плоская, объёмная) фигура. Стороны граней параллелепипеда называются _______________. У параллелепипеда ...Объём шара и площадь сферы
План:. Понятия: Сфера Круговой сектор Шар Шаровой сегмент Шаровой слой Шаровой сектор Формула для вычисления площади сферы Формулы для вычисления ...Объём тел
Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем систему координат – ось ох перпендикулярна ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Объём тела
ρ масса плотность кг с время t m м/с путь скорость инерция v км/ч год г м мин s. . . . . . Архимед. Архиме́д (Ἀρχιμήδης; 287 до н. э.) — 212 до н. ...Конспекты
Площади поверхностей призмы, пирамиды, усеченной пирамиды
Тема урока: «. Площади поверхностей призмы, пирамиды, усеченной пирамиды. ». . Цели и задачи урока. Учебная цель –. закрепить и систематизировать ...Объём прямоугольного параллелепипеда
Предмет:. математика. Класс:. 5. Учитель. : Булатова Анна Васильевна. Базовый учебник:. Муравин Г. К., Муравина О. В. «Математика»,5 класс. ...Объёмы. Объём прямоугольного параллелепипеда
Урок математики в 5 классе. Подклетнева И.В.( МОБУ Гимназия №15 г. Сочи),Боклаг В.Н. (МОБУ СОШ №10 г. Сочи). . Урок математики в 5 классе. Подклетнева ...Объём прямоугольного параллелепипеда
МБОУ Белоберезковская СОШ №1 Трубчевского района Брянской области. Урок по теме «Объём прямоугольного параллелепипеда». 5-й класс. Ананченко ...Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипеда. Цель:. Обобщить, повторить и систематизировать знания по теме: «Объём. Объем прямоугольного параллелепипеда». ...Объём прямоугольного паралле-лепипеда
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2 с.Октябрьское». МО – Пригородный район РСО - Алания. ...Объем наклонного параллелепипеда. Объем призмы
Технологическая карта. Класс – 11. Предмет – геометрия. Тема - Объем наклонного параллелепипеда. Объем призмы. Проверка домашнего задания. ...Объём многогранников. Решение профессионально значимых задач
Авторская работа на тему:. . «Объём многогранников. Решение профессионально значимых задач». Автор работы:. . преподаватель математики выс. ...Объём куба и прямоугольного параллелепипеда. Кубический см
Ленинская средняя школа. Разработка открытого урока математики в 4 классе на тему:. « Объём куба и прямоугольного ...Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда
Конспект урока по математике 4 класс. Тема: «Вычисление периметра и площади прямоугольника. Объём прямоугольного параллелепипеда». Подготовила: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 октября 2018
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию