Конспект урока «Площади поверхностей призмы, пирамиды, усеченной пирамиды» по математике
Тема урока: «Площади поверхностей призмы, пирамиды, усеченной пирамиды»
Цели и задачи урока
Учебная цель – закрепить и систематизировать пройденный материал;
-ввести понятия площади поверхности призмы, площади поверхности пирамиды, площади поверхности усеченной пирамиды;
Воспитательная цель -прививать любовь к знаниям;
- воспитывать ответственность и активность;
Развивающая цель – сформировать навыки использования знаний при решении задач.
Тип урока -комбинированный.
Оформление – плакаты, геометрические фигуры, цветные фишки, линейка, таблица, раздаточный материал.
Ход урока
Организационный момент - Приветствие с учениками группы, проверка готовности аудитории к уроку, росписи в бегунке.
 I. Устная работа
I. Устная работа
1.Среди изображенных тел выберите те, которые являются призмами.
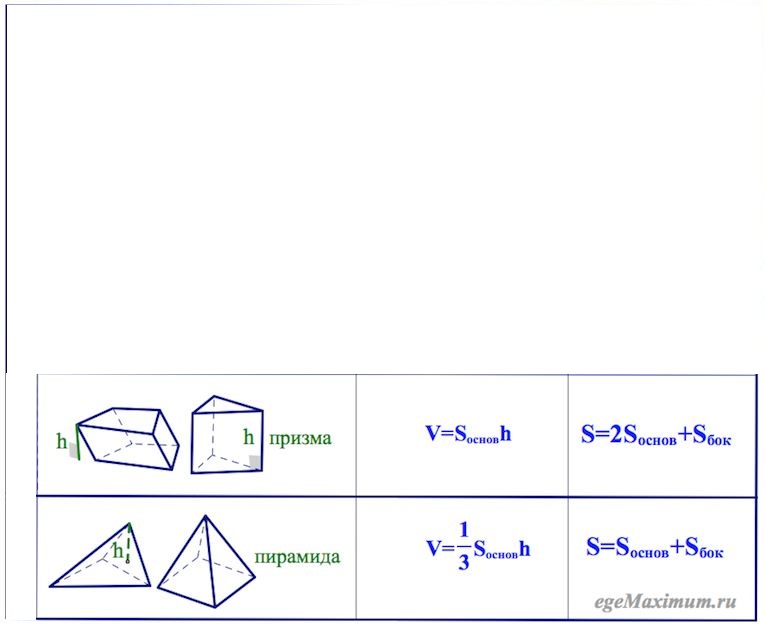
2. Назовите для призмы: вершины
основания
боковые ребра
боковые грани
противоположные грани
диагонали призмы
диагональные сечения
3.Среди изображенных тел выберите те, которые являются пирамидами.
4. Назовите для пирамиды: основание пирамиды
высоту
апофему
диагональные сечения
| Наименование многогранника | В | Р | Г | Эйлерова характеристика ( В-Р+Г) | |
| 1 | 4-хугольная призма | | | | |
| 2 | 4-хугольная пирамида | | | | |
| 3 | 3-угольная пирамида | | | | |
| 4 | | | | | |
| 5 | n-угольная призма | | | | |
| 6 | n-угольная пирамида | | | | |
| | | | | | |
В- число вершин многогранника,
Р- число ребер многогранника,
Г- число граней многогранника.
Нами изучаются многогранники, Эйлерова характеристика которых равна 2.
Это равенство верно для произвольного выпуклого многогранника
(доказано Л.Эйлером в 1752 г.)
Вопросы для проверки знаний формул :
-
Напишите формулу для вычисления объема призмы.
-
По какой формуле вычисляется объем пирамиды?
-
По какой формуле вычисляется объем цилиндра?
-
По какой формуле вычисляется объем конуса?
-
Напишите формулу для вычисления объема усеченной пирамиды.
II. Проверка знаний пройденного материала (путем решения задач с многогранниками и телами вращения).
1.Образующая конуса равна 6см и наклонена к плоскости основания под углом в 300 . Найдите объем конуса. (Ответ: V=9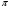 см3 )
см3 )
2. Прямоугольный параллелепипед имеет три измерения a=5см, в=8см, с=10см.
Найдите диагональ параллелепипеда. (Ответ: d=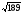 cм)
cм)
3.Площадь основания правильной четырехугольной пирамиды равна 144см2 . Все боковые ребра равны 9см. Найдите объем пирамиды. (Ответ: V=144cм3)
. Все боковые ребра равны 9см. Найдите объем пирамиды. (Ответ: V=144cм3)
4. Шар радиус которого 5дм, пересечен плоскостью на расстоянии 3дм от центра.
Найдите площадь сечения. (Ответ: Sсеч. = 16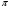 дм2)
дм2)
III. Объяснение нового материала.
«Площади поверхностей призмы, пирамиды, усеченной прамиды»
Площадь полной поверхности призмы равна сумме площадей ее боковой поверхности и площадей ее оснований, т.е. S.п.п=Sб.п +2Sосн
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту, т.е. на длину бокового ребра.
S.б.п=PH
где Р- периметр основания, H – высота призмы.
Доказательство:
Теорема. Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра .
S.б.п=PсечH
Площадь полной поверхности пирамиды равна сумме площадей ее боковой поверхности и площади основания. S.п.п=Sб.п +Sосн
Теорема. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему, т.е.
S.б.п=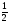 P
P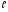 ,
,
где Р – периметр основания, а 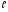 - апофема пирамиды.
- апофема пирамиды.
Доказательство:
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему, т.е.
S.б.п=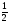 (аn+bn)
(аn+bn)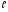 ,
,
где an, bn – периметры основания, а 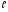 - апофема.
- апофема.
IV.Закрепление нового материала.
Выберите правильный ответ из числа предложенных.
1.Чему равна площадь полной поверхности куба с ребром 6см?
А)36см2 ;б)144см2; в)216см2; г) 144см2.
2.Чему равна площадь боковой поверхности правильной четырехугольной призмы, если ее высота h, сторона основания 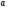 ?
?
А) hа; б) 4аh; в) 42h; г) 4(а+h).
3.Прямоугольный параллелепипед имеет три измерения, равные а=5см; в=8см; h=10cм.
Какова площадь его полной поверхности?
А) 400см2; б) 160см2; в) 280см2; г) 340см2.
4.Чему равна апофема правильной четырехугольной пирамиды со стороной основания 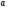 и высотой h?
и высотой h?
А) 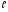 =
=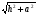 ; б)
; б) 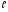 =
=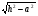 ; в)
; в) 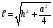 .
.
5.Чему равна высота правильной шестиугольной пирамиды со стороной основания 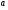 и боковым ребром
и боковым ребром 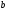 ?
?
А) h=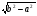 ; б) h=
; б) h=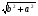 ; в) h=
; в) h=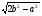 .
.
Задача1.Образующая конуса равна 6см и наклонена к плоскости основания под углом в 300 . Найдите объем конуса.
Задача2. Прямоугольный параллелепипед имеет три измерения a=5см, в=8см, с=10см.
Найдите диагональ параллелепипеда.
Задача3. Площадь основания правильной четырехугольной пирамиды равна 144см2 . Все боковые ребра равны 9см. Найдите объем пирамиды.
. Все боковые ребра равны 9см. Найдите объем пирамиды.
Задач4. Шар радиус которого 5дм, пересечен плоскостью на расстоянии 3дм от центра.Найдите площадь сечения.
V. Домашнее задание:Доказать теорему. Решить задачи:
Дано:SABCD-пирамида, Дано: SABCD-пирамида,
АВСD-ромб, ABCD-ромб,
АВ=BD, PABCD=16, АС=6, BD=8,
SO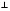 (ABC), SO=1. SO
(ABC), SO=1. SO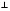 (ABC), SO=1.
(ABC), SO=1.
Найти: Sб.п.-? Найти: Sп.п-?
VI. Подведение итогов урока.
Здесь представлен конспект к уроку на тему «Площади поверхностей призмы, пирамиды, усеченной пирамиды», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

