Конспект урока «Площади многоугольников. Решение задач» по математике для 8 класса

8 класс

Тема:Площади многоугольников. Решение задач.

Цель урока:

1. Обобщить знания о площадях многоугольников.

2. Рассмотреть различные способы нахождения площадей многоугольников на клетчатой бумаге.

3. Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать самостоятельно, в группе, осуществлять самоконтроль.

Задачи урока

1. Повторим все известные нам формулы площадей многоугольников

2. Решитьзадачи на нахождение площадей используя только формулы

3. Научиться решать задачи нового типа

Ход урока.

I. Организационный момент.

Здравствуйте, рада приветствовать всех собравшихся в этой аудитории. Сегодня я проведу у вас урок геометрии. Я пожелаю вам и себе учебной плодотворной работы. Эпиграфом к нашему занятию я взяла слова великого итальянского физика и астронома Галилео Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Как вы думаете, почему он так говорил о геометрии? Молодцы!

Но прежде чем мы начнем урок, я хочу предложить вам одну цитату из анализа работ ЕГЭ по математике: «Традиционно на экзамене наибольшую трудность у выпускников вызывают геометрические задачи» (из анализа результатов ЕГЭ по математике)

Поднимите руки те, у кого не возникают затруднения при решении геометрических задач. Молодцы, я рада за вас.

Поэтому сегодня я приготовила для вас задания, встречающиеся в ЕГЭ. А теперь давайте вспомним, какую тему вы изучали на последних уроках?

На предыдущих уроках вы изучали тему «Площади многоугольников. Решение задач».

Ребята, давайте сформулируем цель нашего урока.

Актуализация опорных знаний

А что вы уже знаете по данной теме?

Какие сведения ассоциируются у вас с этой темой?

Возможные ответы учащихся:

1. Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.

2. Площади измеряются в квадратных единицах измерения.

3. Свойства площадей:

• Равные многоугольники имеют равные площади.

• Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

• Площадь квадрата равна квадрату его стороны.

4. Площадь прямоугольника равна произведению его смежных сторон.

5. Площадь параллелограмма равна произведению его основания на высоту.

6. Площадь треугольника равна половине произведения его основания на высоту.

7. Площадь прямоугольного треугольника равна половине произведения его катетов.

8. Если высоты треугольников равны, то их площади относятся как основания.

9. Теорема об отношении площадей треугольников, имеющих по равному углу: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

10. Площадь трапеции равна произведению полу суммы её оснований на высоту.

2. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Хорошо. А теперь я вам предлагаю ваши знания по данной теме представить в виде небольшой памятки, которую можно будет использовать в дальнейшем. Для этого у вас лежит на столе шаблон, который необходимо заполнить.

Сравнение и корректировка шаблонов. Оцените свою работу на данном этапе урока в листах оценивания.

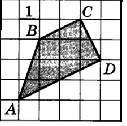
Итак, мы с вами повторили необходимые нам теоретические сведения и можем перейти к решению задач. У вас на столах лежат листы с заданиями из открытого банка заданий ЕГЭ по математике. Вы должны вычислить площади заданных многоугольников.

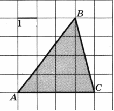
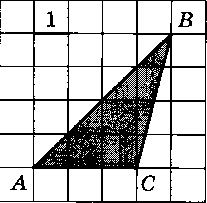
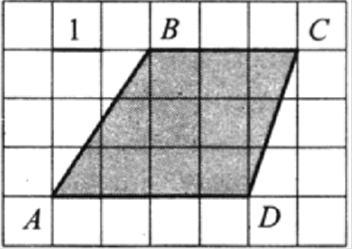
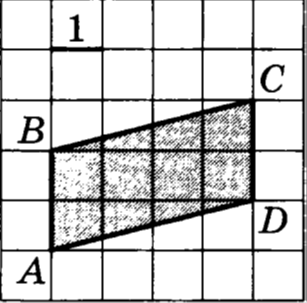
Внимательно прочтите задание. С помощью единичной клетки найти длины отрезков, необходимые для вычисления площади и вычислить площадь многоугольника. Каждой команде дается лист с заданиями.

Обсуждение.

Давайте посмотрим, что у вас получилось? Кто готов назвать площади фигур? Ребята, кто может объяснить, как найти площадь первой фигуры? Исследовательская часть.

1.Постановка проблемы. Чему равна площадь трапеции (мы не смогли вычислить) Почему? Вы не знаете формулы площади трапеции? Тогда почему мы не можем вычислить площадь трапеции с помощью формулы? Можно ли воспользоваться тем же способом вычисления площади трапеции, что и для остальных фигур? (Вывод: У всех этих многоугольников необходимые элементы для вычисления площади явно измеряются и выражаются натуральным числом.) Итак, ребята, с какой проблемой вы столкнулись?

Как вы считаете, эта задача решаема? А существует ли какой-то способ решения таких задач? А давайте попробуем найти эти способы.

Я предлагаю вам провести свое исследование по нахождению площади заданного треугольника. Время на исследование 5 минут.

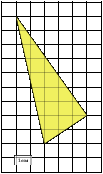
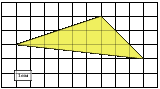
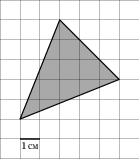
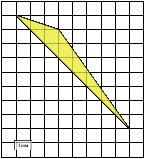
У вас на столах лежит листок заданием: Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Попробуйте провести свое исследование и найти способ вычисления площади данного треугольника.

Идет работа в группах.

А теперь я предлагаю группам представить способ, которым они решили свою задачу. Ребята объясняют способы, с помощью которых они нашли площади треугольников.

Оцените свою работу на данном этапе урока в листах оценивания.

А теперь давайте вернемся к нашей трапеции. Как вы думаете, теперь мы сможем найти площадь данной трапеции? А давайте проверим. (Учащиеся вычисляют площадь трапеции).

А теперь давайте сравним полученные результаты. Каким способом находила площадь 1 группа?.......

Заключение.

Вывод: итак, давайте обобщим, каким же способом можно вычислить площадь многоугольника на клетчатой бумаге? Вы – молодцы, ведь вы успешно справились с выполнением типа задач, который был вам неизвестен. А дома я предлагаю вам выполнить творческое задание: подготовить подобные задания и решить их.

Рефлексия:

Учитель: Наш урок подходит к концу ребята, давайте вспомним, какова была цель нашего занятия().

Как вы думаете, мы достигли этой цели?

Какие способы решения заданий вы запомнили? В чем их суть?

Какой способ вам наиболее понравился? Почему?

В листах самооценки оцените себя.

Поднимите руки, у кого сегодня все получилось? Молодцы я рада за вас. А у кого возникли затруднения? Можете объяснить их причину? Ребята, вы сегодня все были молодцы, вы очень хорошо поработали, спасибо вам огромное за урок.