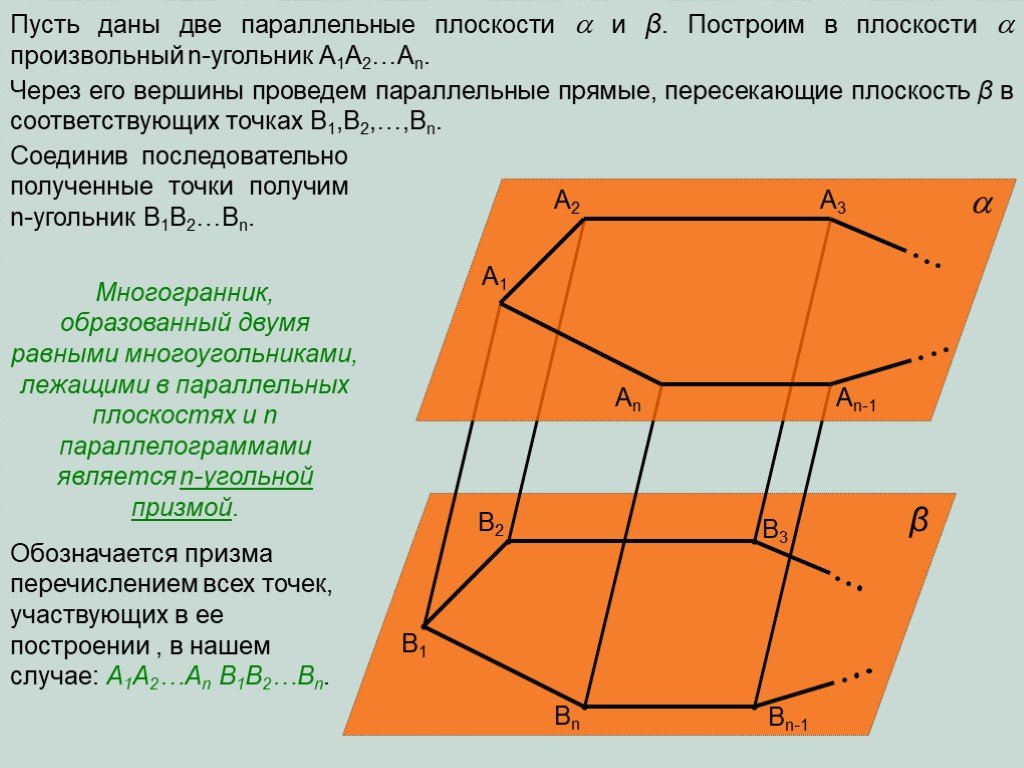
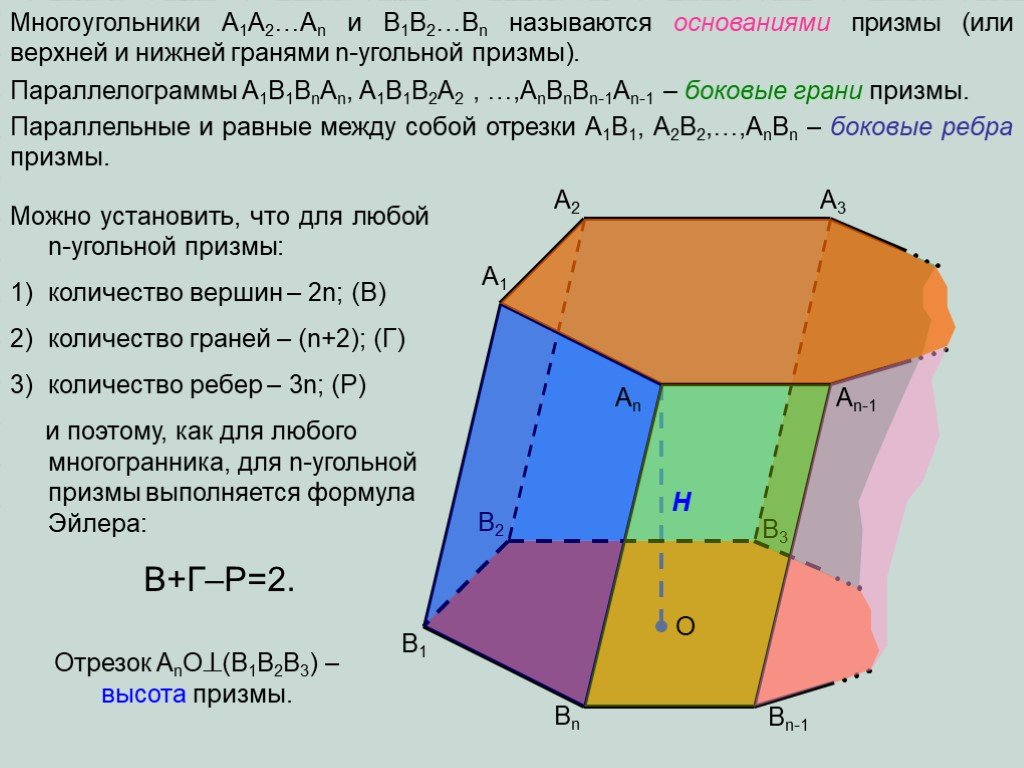
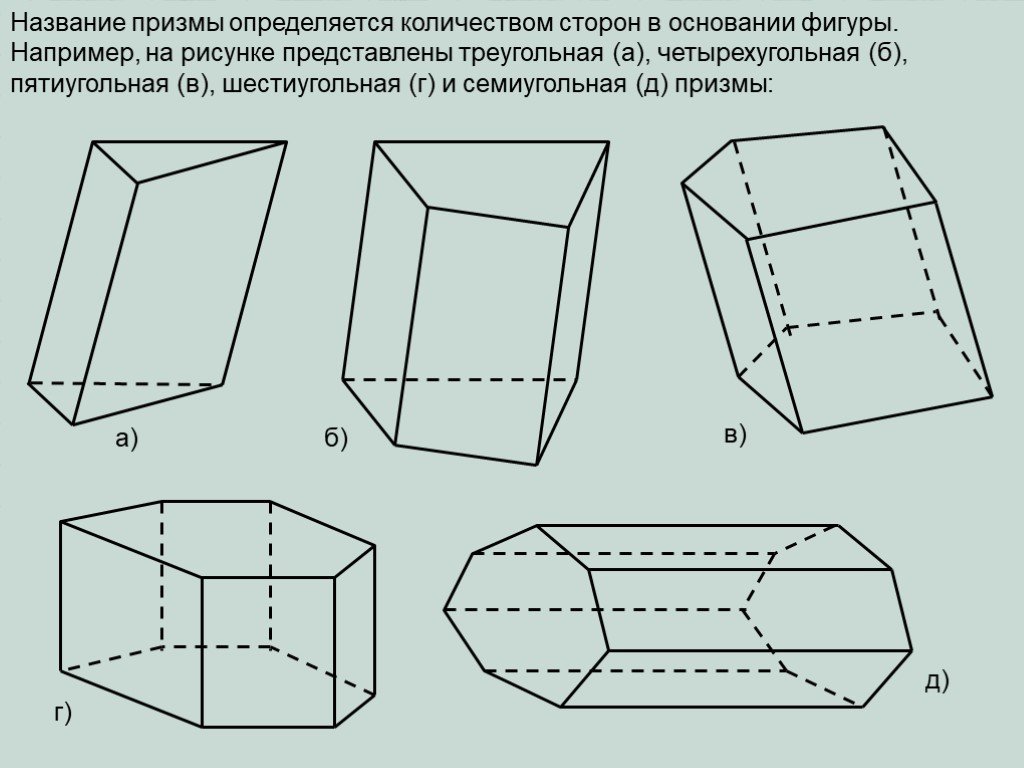
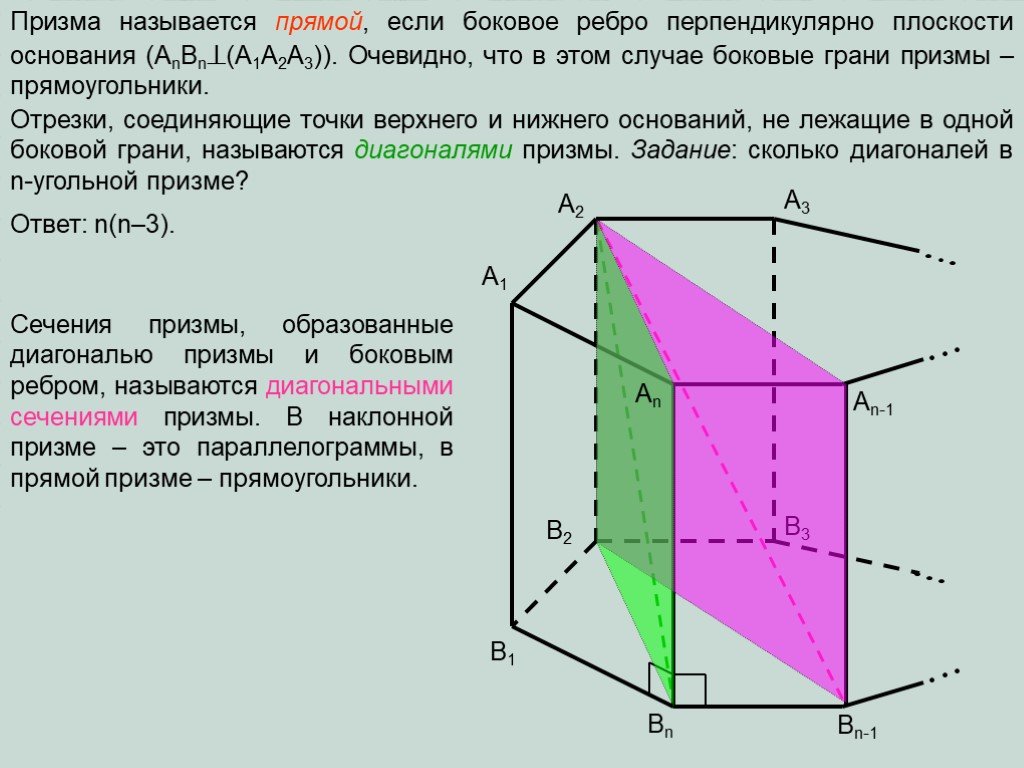
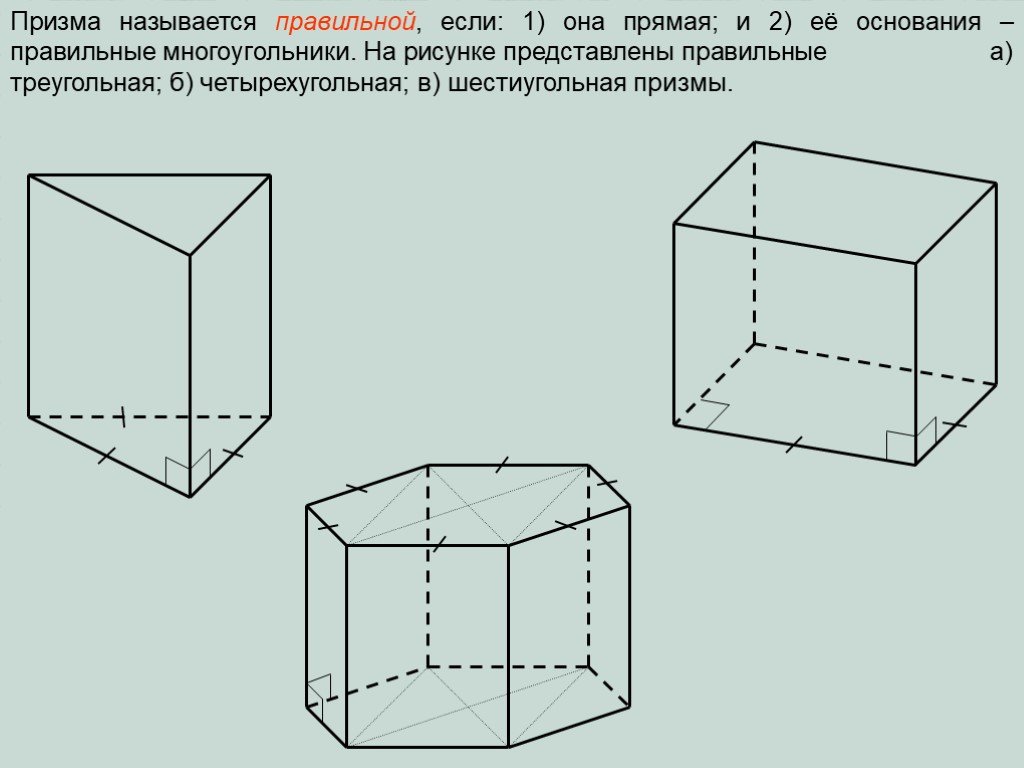
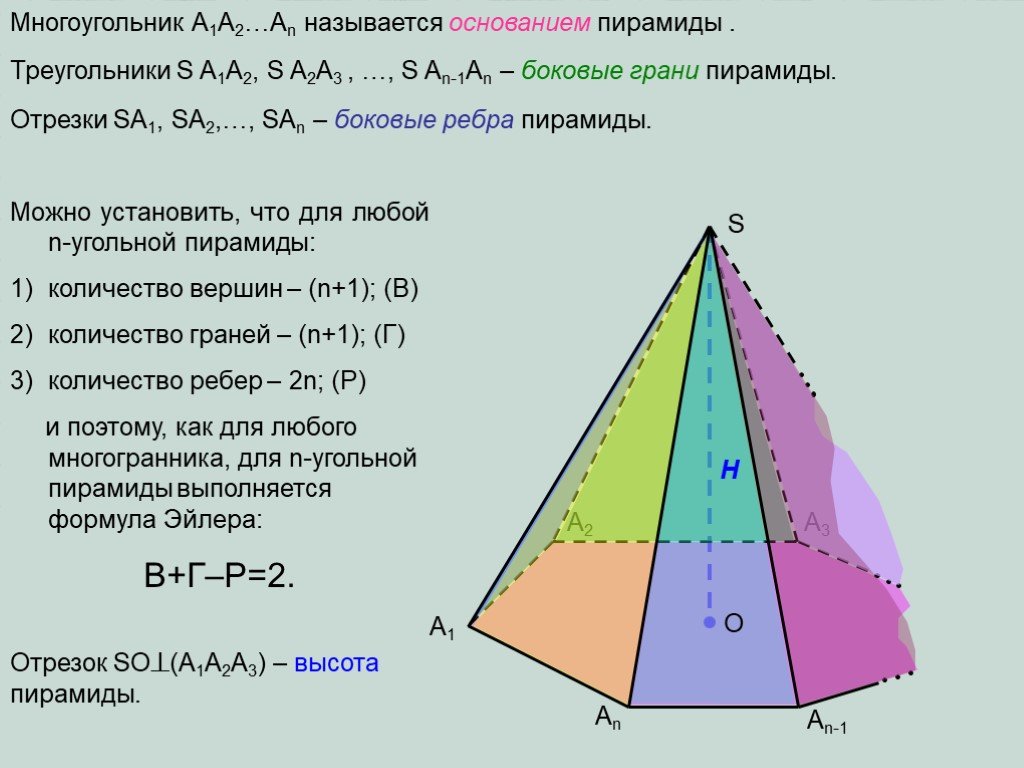
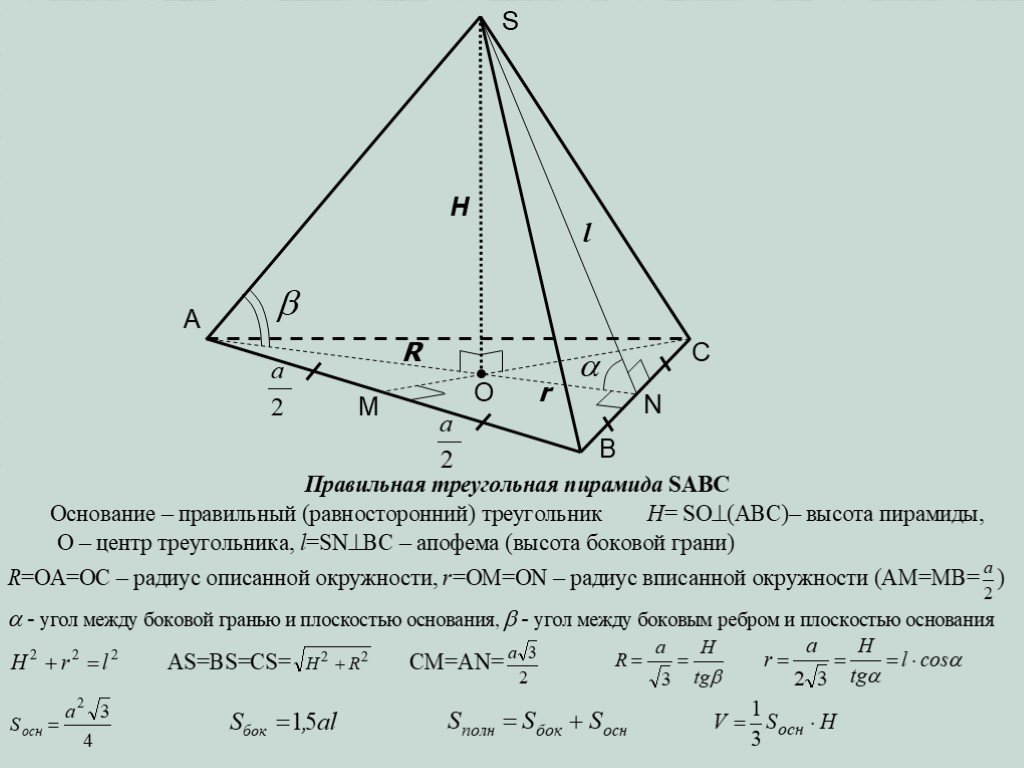
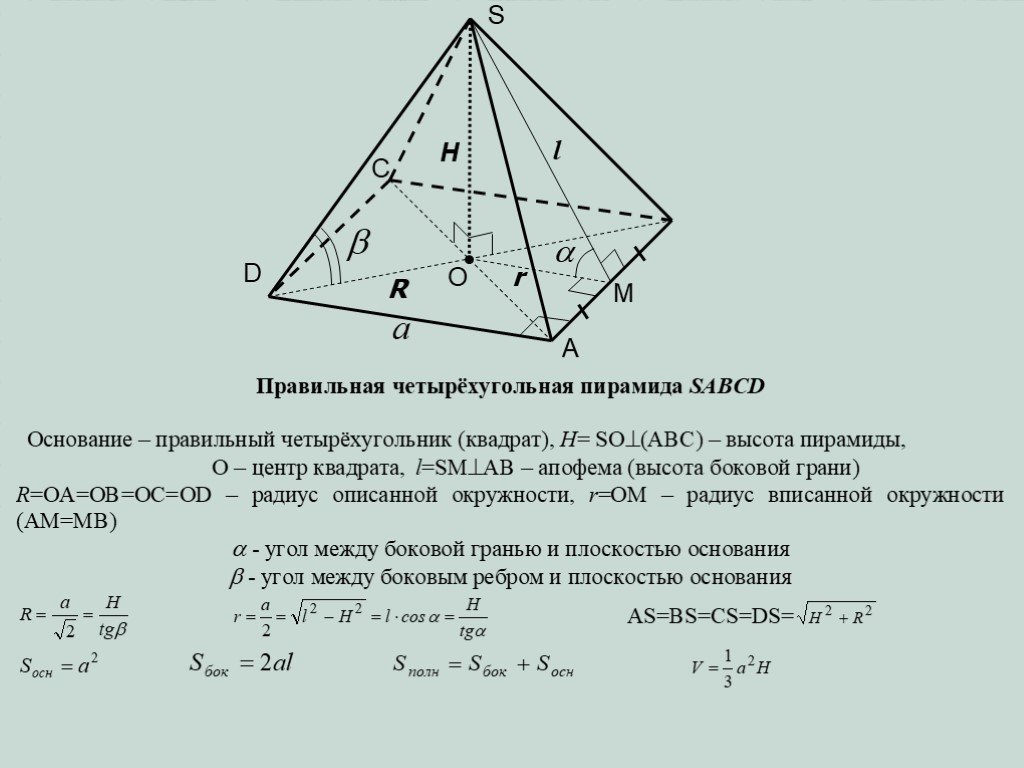
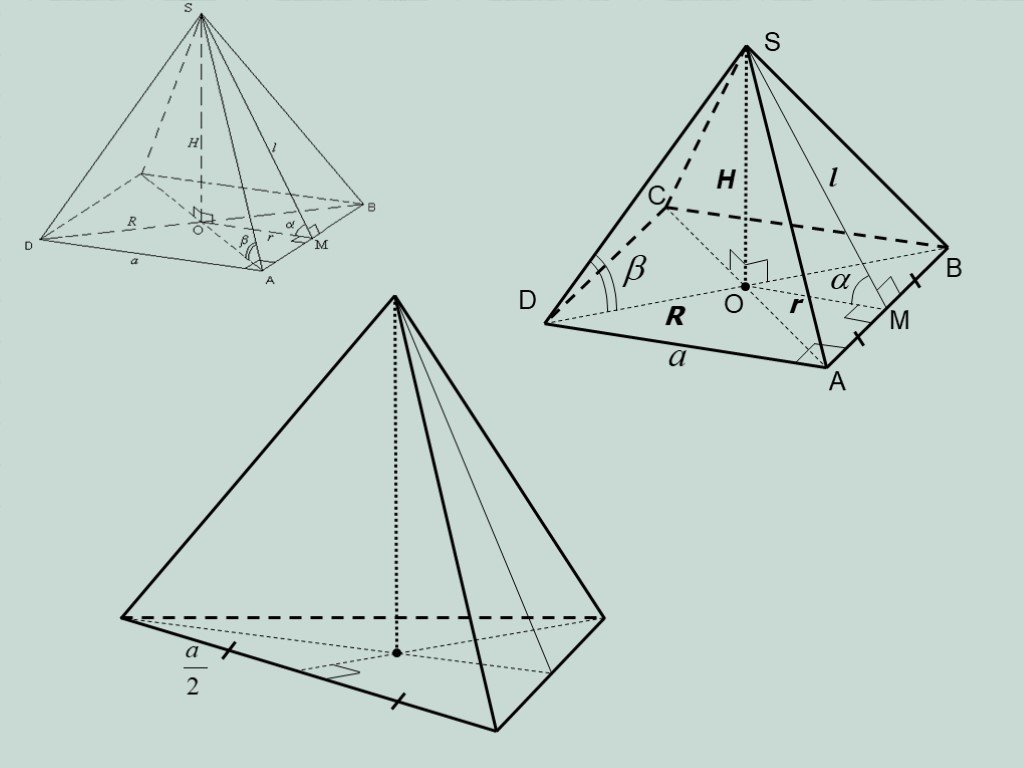
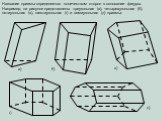
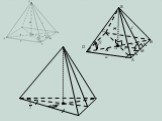
Презентация "Определение призмы, пирамиды" по математике – проект, доклад
Презентацию на тему "Определение призмы, пирамиды" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение задач на комбинации призмы, шара и пирамиды
Шар, вписанный в пирамиду. В любую треугольную пирамиду можно вписать шар; В пирамиду, у которой в основание можно вписать окружность; центр, которой ...Свойства пирамиды с равными боковыми ребрами
Теорема 1.1. Дано: МАВС - треугольная пирамида, МО – высота пирамиды, боковые ребра равны АМ=ВМ=СМ. Доказать: АО = ВО = СО. Теорема 1.2. Дано: МАВС ...Призма. Построение сечений призмы плоскостями
План урока. Тема: Призма. Построение сечений призмы плоскостями. Цель: Дать определение призмы. Научить строить сечения призмы плоскостями. Оборудование: ...Площадь поверхности призмы
Основанием треугольной призмы является равнобедренный прямоугольный треугольник. Ровно одна ее грань — квадрат, известны длины ее ребер и высота. ...Определение степени с натуральным показателем
Тема: Определение степени с натуральным показателем. Цели: • • Закрепить умение вычислять степень числа, умение выполнять вычисления, зная порядок ...Определение синуса, косинуса, тангенса и котангенса
Цели урока:. 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров и задач. 3.Привитие ...Определение подобных треугольников
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ. D А В С. № 1. Пропорциональны ли отрезки АВ=2см и СD=4см отрезкам А1В1=3см и С1D1=6 см. Свойство пропорции: произведение ...Объем призмы
Ход урока:. Вступительное слово учителя Повторение материала проводится в форме игры «Поле чудес Правила игры: выбор троек игроков после правильного ...Объём призмы
ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ: I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы. Объем каждого тела выражается положительным ...Объем пирамиды
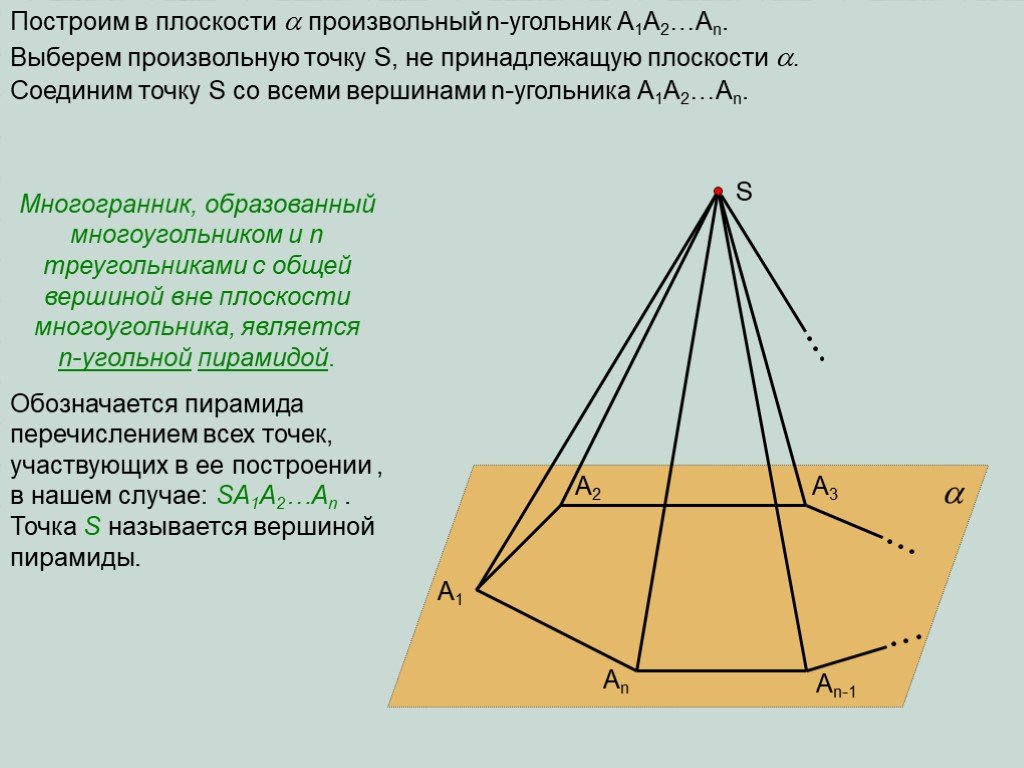
Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Объем пирамиды
Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Сечения призмы
Виды призм. Прямая. Правильная. Наклонная. Все призмы делятся на прямые и наклонные. Если боковое ребро призмы перпендикулярно плоскости ее основания, ...Определение параллельных прямых
. . . Составьте конспект п. 24. Вопрос Какие прямые называются параллельными? Изобразите и обозначьте параллельные прямые Какие отрезки называются ...Объем прямой призмы
Теорема: объем прямой призмы равен произведению площади основания на высоту. Доказательство. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ ...Определение производной
Производной функции y=f(x) называется предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится ...Объем прямой призмы
Цели урока:. Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике. Призма ...Определение степени с натуральным показателем
«Веселые старты» среди 1-2 классов. «Веселые старты» среди 3-4 классы. Шахматы среди 5-х классов. Настольный теннис среди 6-7 классов. Баскетбол среди ...Конспекты
Площади поверхностей призмы, пирамиды, усеченной пирамиды
Тема урока: «. Площади поверхностей призмы, пирамиды, усеченной пирамиды. ». . Цели и задачи урока. Учебная цель –. закрепить и систематизировать ...Определение степени с натуральным показателем
Урок алгебры в 7 классе. . по теме «Определение степени с натуральным показателем». . в рамках проведения. . Всероссийского открытого урока ...Определение степени с натуральным показателем
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №13». муниципального образования г. Братска. ...Определение подобных треугольников
Урок по геометрии в 8 классе. «Определение подобных треугольников». Цель. 1. Ввести новые понятия: отношение отрезков, пропорциональные отрезки, ...Объем пирамиды
Коспект урока по геометрии в 11 классе «Объем пирамиды». Цели занятия:. 1. . Образовательные:. • ознакомление учащихся с геометрическим телом – ...Проекция вершины пирамиды на плоскость основания
Метод проектов. . Проекция вершины пирамиды на плоскость основания. Тип:. исследовательский. Учебный предмет:. геометрия. Участники:. 10 класс. ...Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Определение числа глагола. Изменение глаголов по числам
Русский язык (3-й класс). Тема: «Определение числа глагола. Изменение глаголов по числам». Учитель начальных классов:. ...Определение квадратного уравнения. Неполные квадратные уравнения
План-конспект. урока по математике в 8 классе. «Определение квадратного уравнения. Неполные квадратные уравнения». Составила учитель ...Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии
Тема урока:. «Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии». . Класс:9б. . Дата урока:10.02.2014. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию