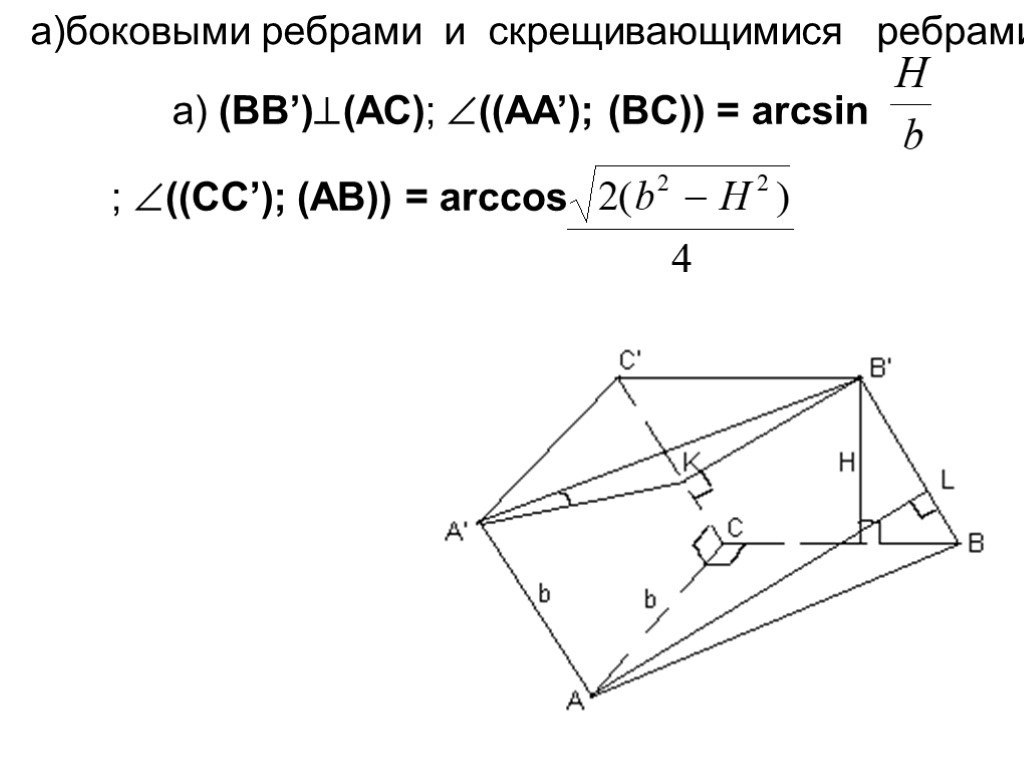
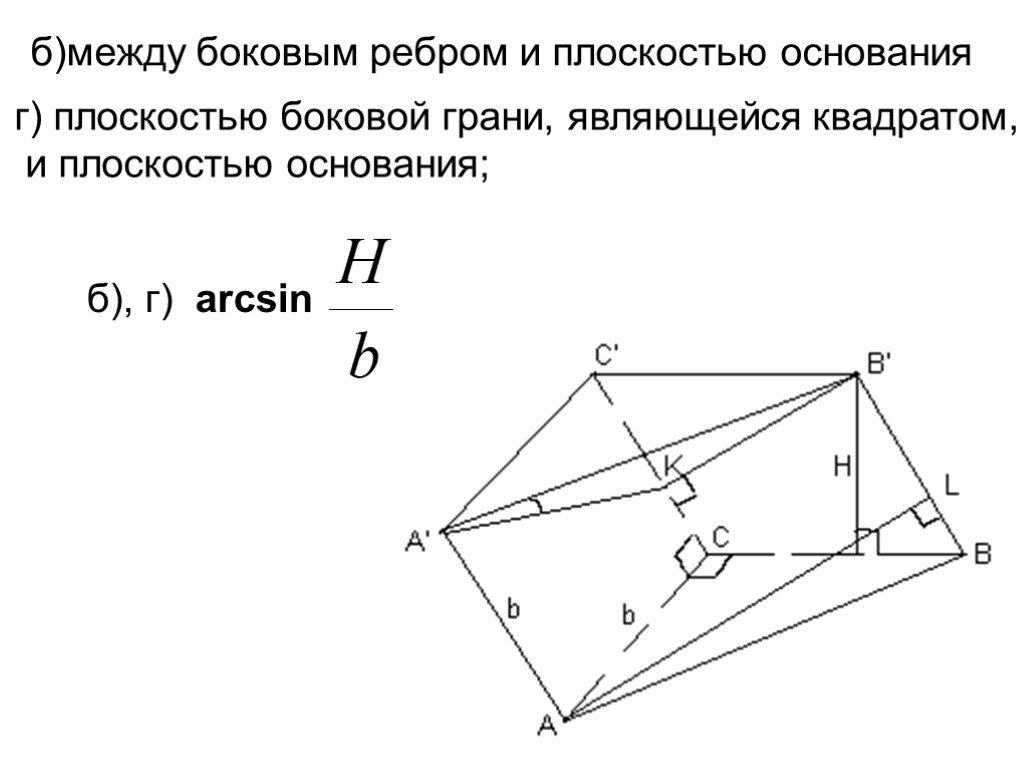
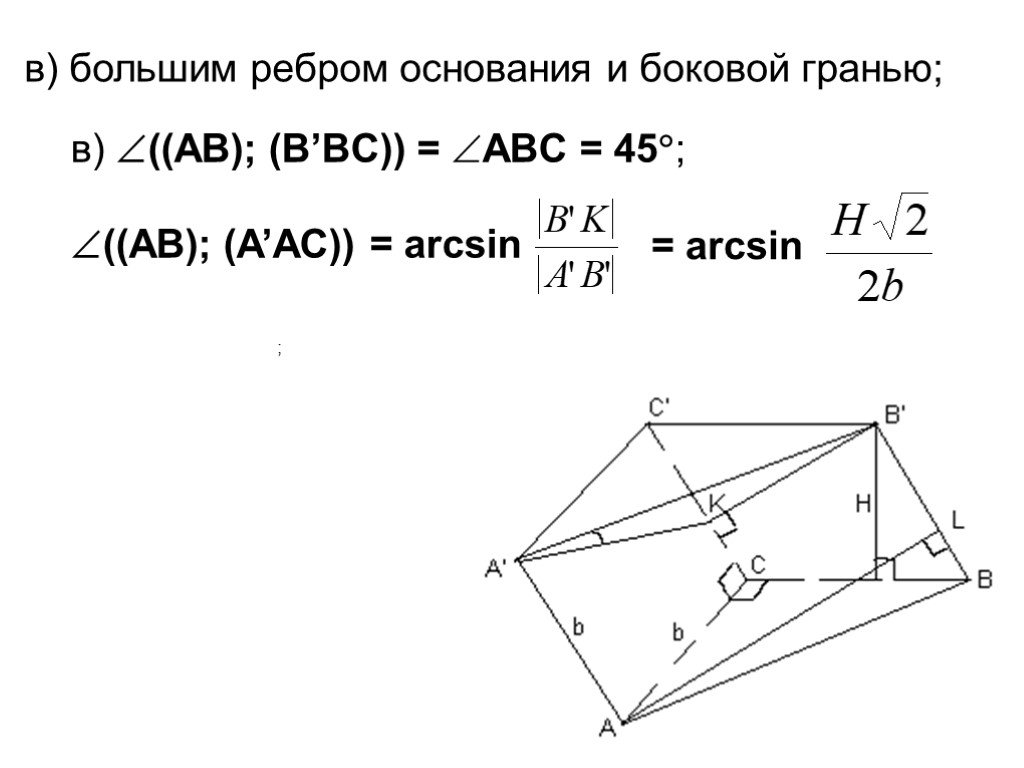
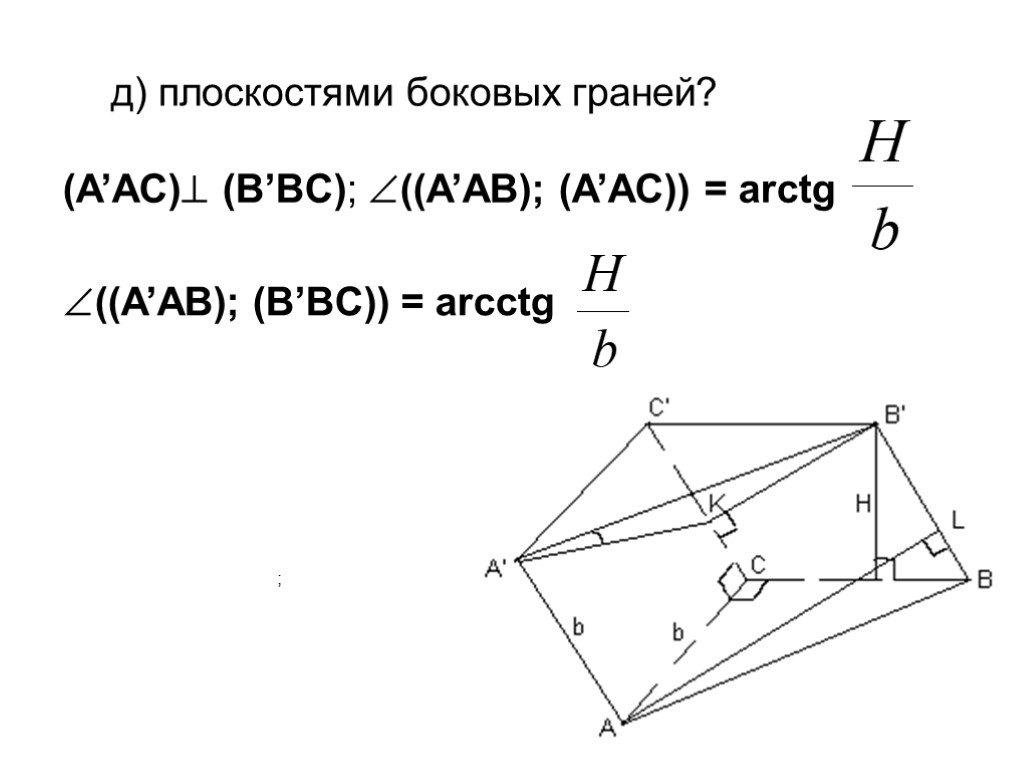
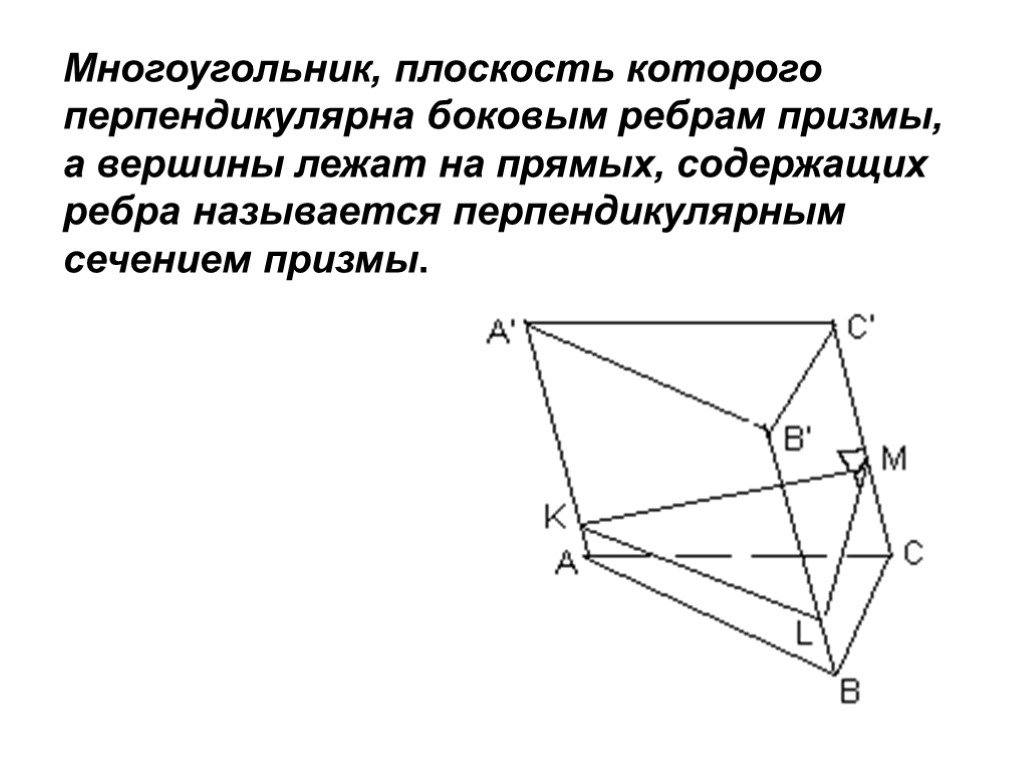
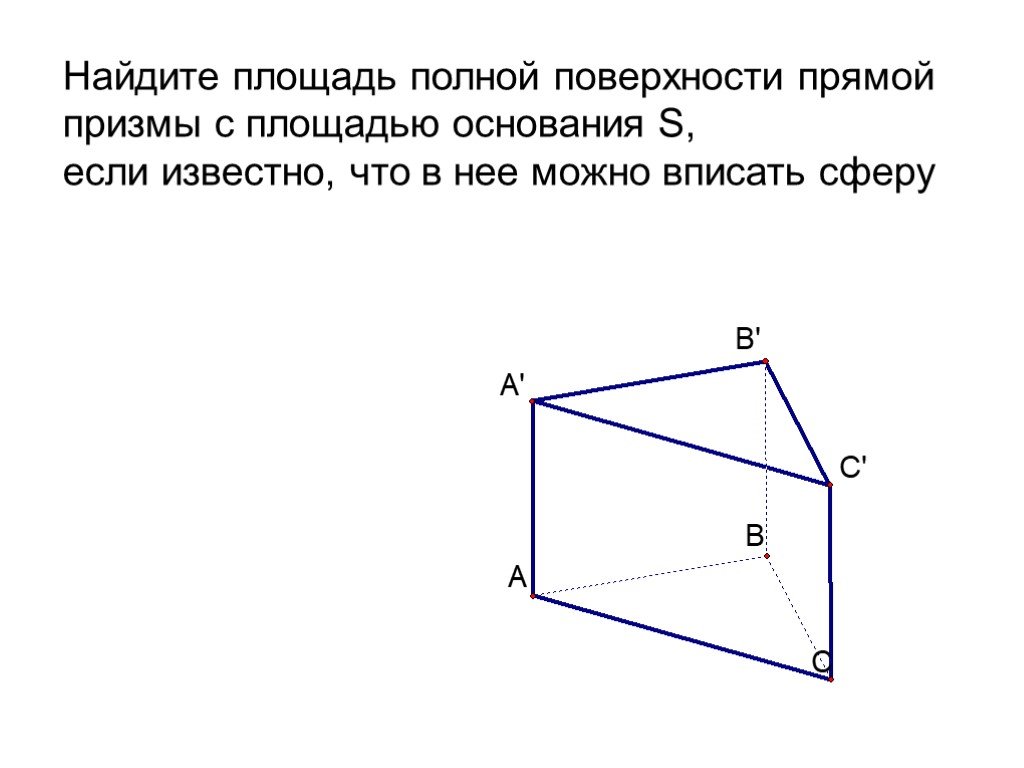
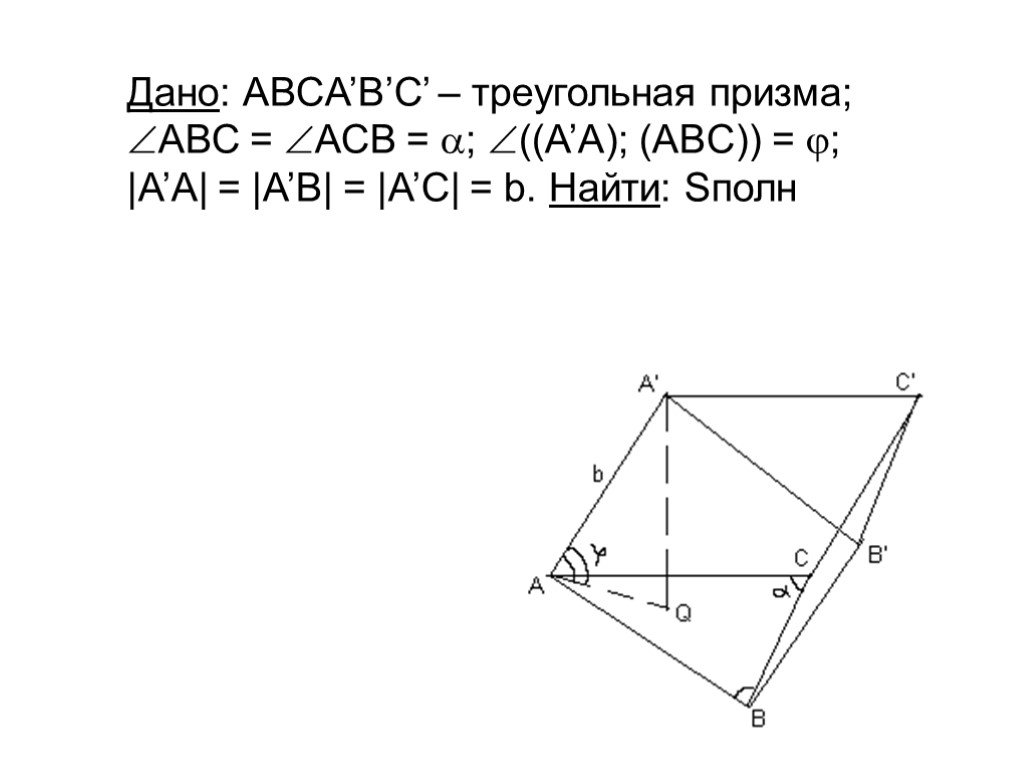
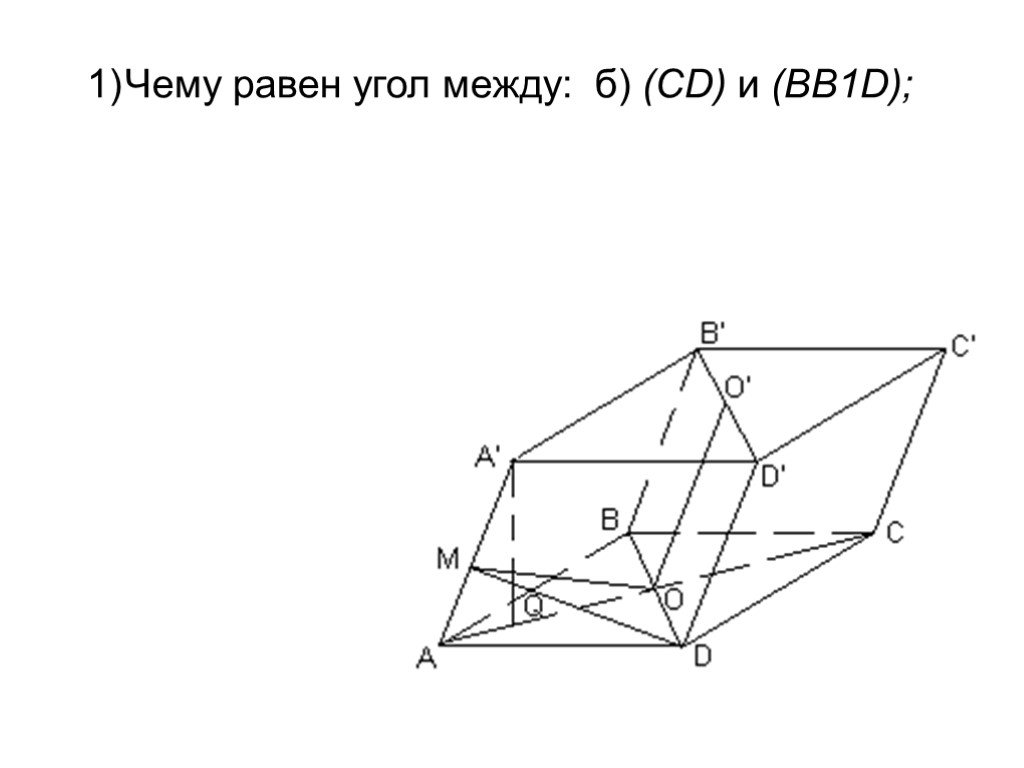
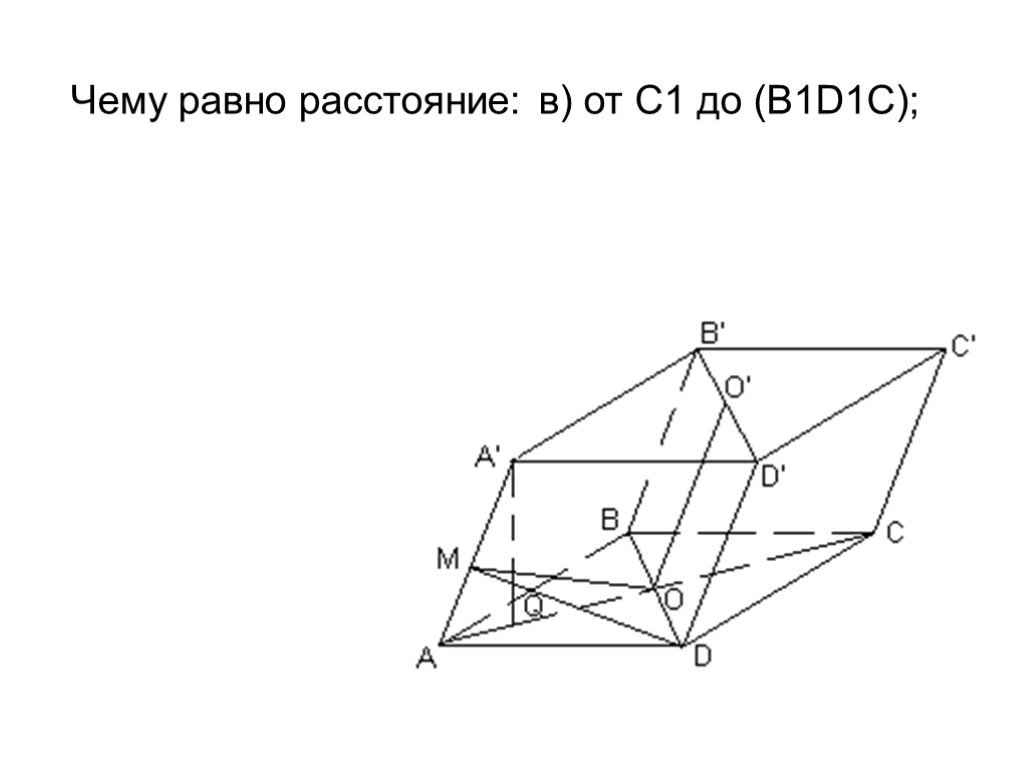
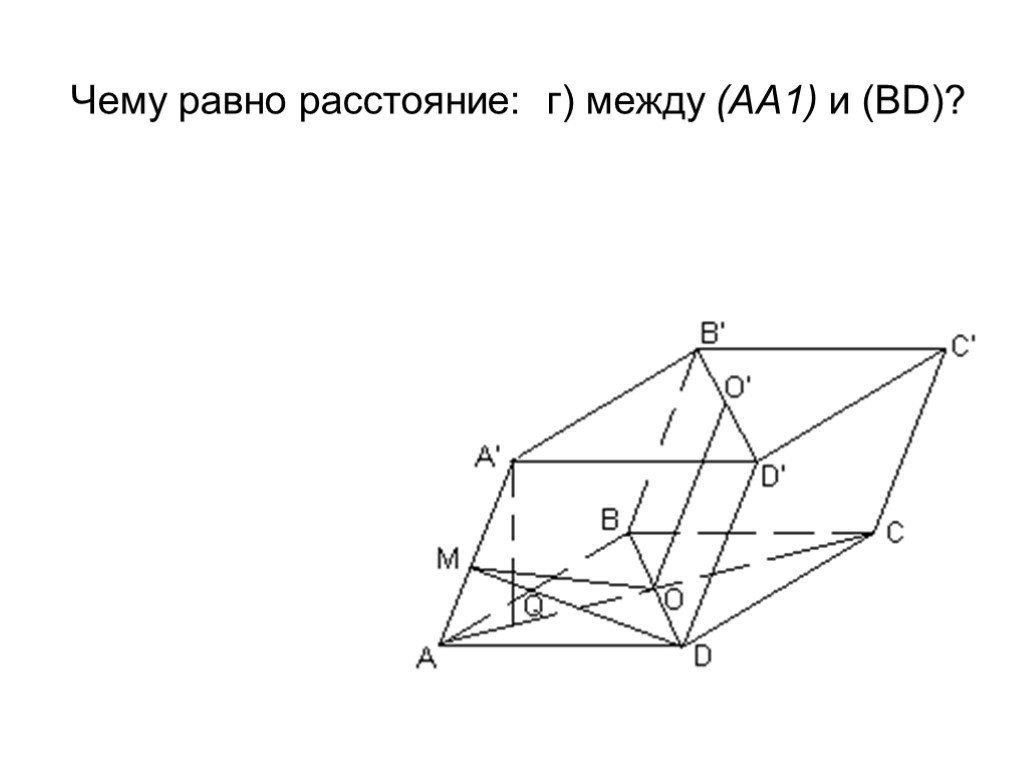
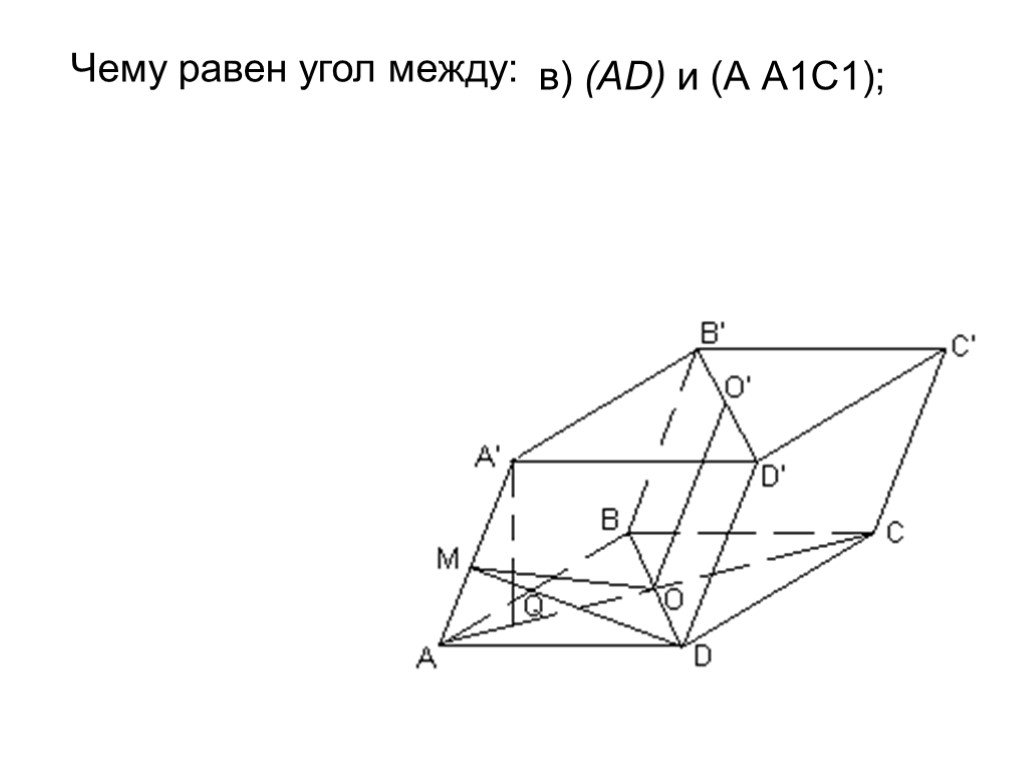
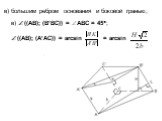
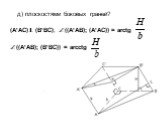
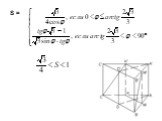
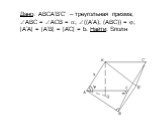
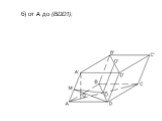
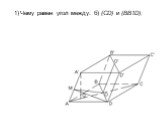
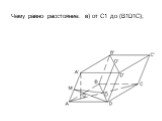
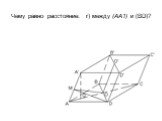
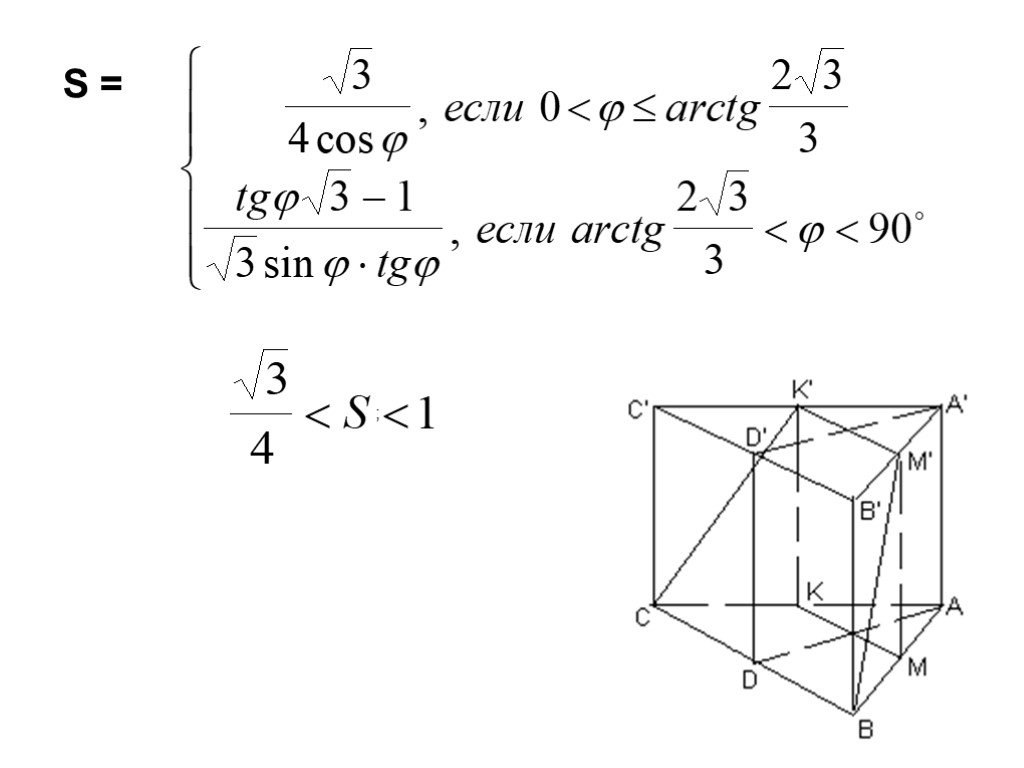Презентация "Площадь поверхности призмы" по математике – проект, доклад
Презентацию на тему "Площадь поверхности призмы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Площадь поверхности конуса
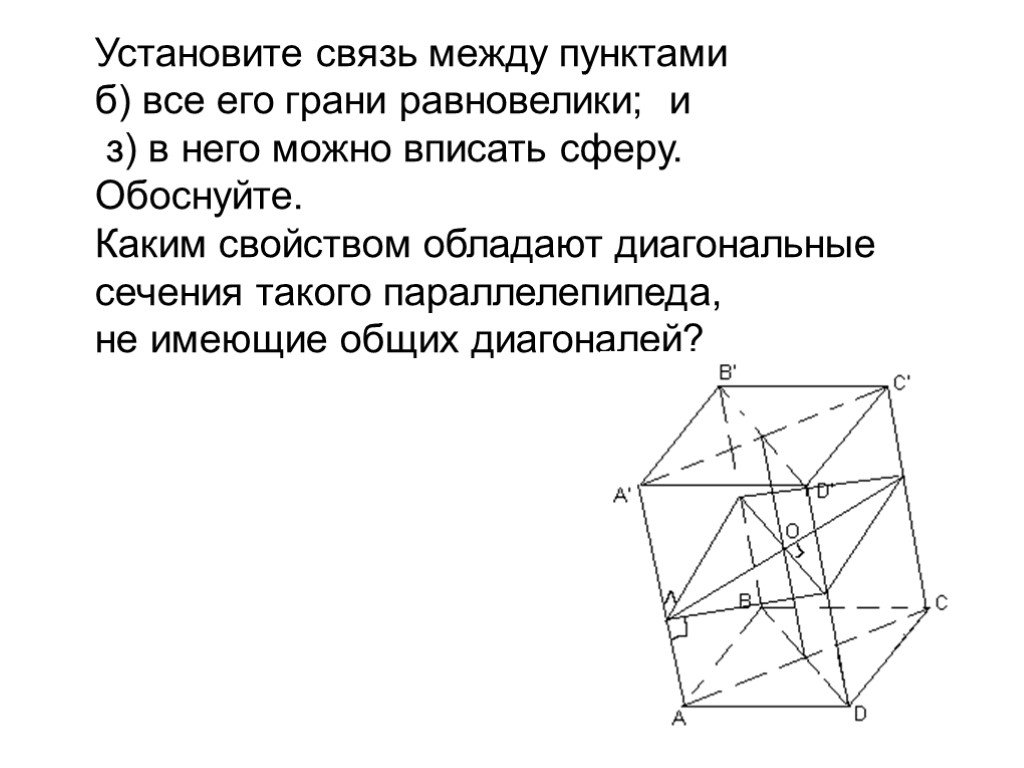
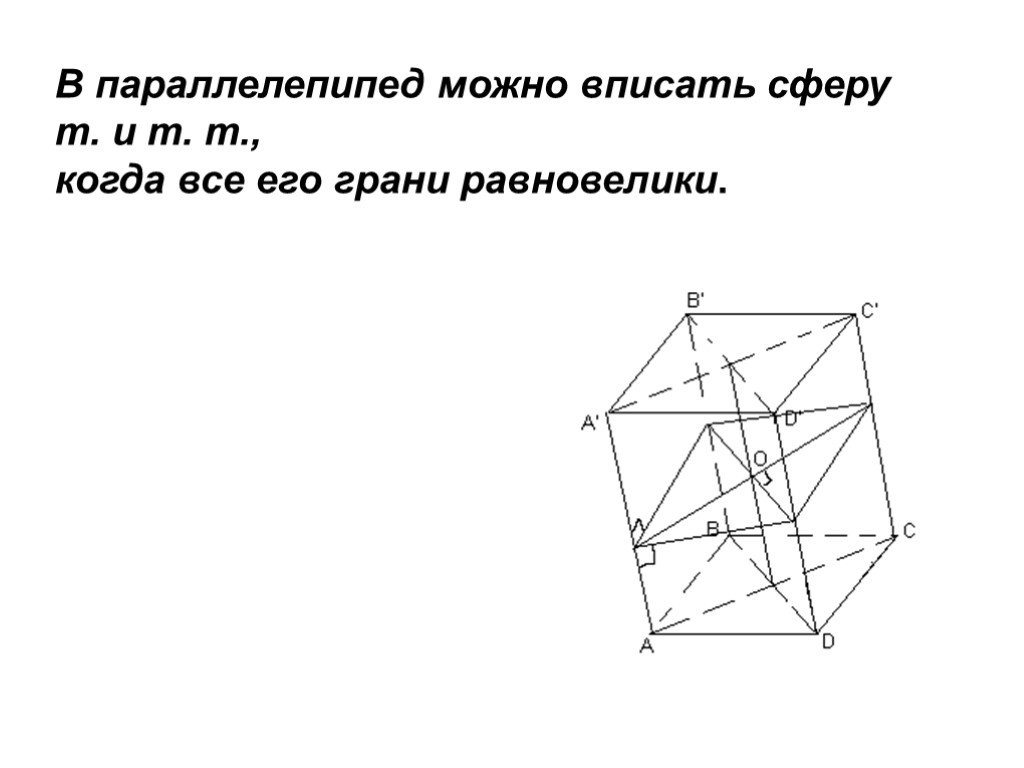
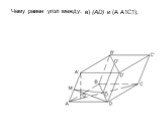
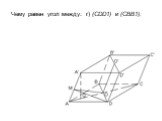
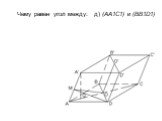
Угадайте зашифрованное тело вращения:. КОНУС – ТЕЛО ВРАЩЕНИЯ. Δ КОВ : КО – ось вращения. К О В. КОНУС. OK=H (высота конуса) OA=OB=OC=R (радиус основания ...Площадь прямоугольника: практикум
СРЕДИ ФИГУР, ПРИВЕДЕННЫХ НА РИСУНКЕ, УКАЖИТЕ:. а). равные фигуры б). фигуры равной площади. А Б В Г. в). площадь каждой фигуры. Чему равна площадь ...Площадь параллелограмма, треугольника, трапеции
Вычисление площадей фигур на клетчатой бумаге.1 3 4 5 6 7 8 9 10 11. Найдите площадь фигуры:.
Ответ: 6 см² №1. №2. 12 см² №3. №4. 28 см² №5. №6 ...
Площадь параллелограмма
Цели урока. дать определение высоты параллелограмма ; доказать теорему о площади параллелограмма; показать применение формулы в процессе решения задач. ...Площадь многоугольников
Многоугольник A B C D K L M N параллелограмм трапеция J B I P R. A D Z X H Y M N K T прямоугольник ромб квадрат. ПЛОЩАДЬ ТРАПЕЦИИ. Площадь трапеции ...сечение поверхности
Алгоритм решения задачи. 1. Объекты ( и ) рассекают вспомогательной секущей плоскостью Г. 2. Находят линию пересечения вспомогательной плоскости ...Площадь фигуры
Старая сказка на новый лад. Сказка - умница и прелесть, с нами рядышком жив ёт... Сосчитай, разгадай! 97 - 89 = 36 : 6 = 53 - 48 = 42 : 6 = 12 : 4 ...Площадь трапеции
Трапеция. ВС параллельна АД, АВ не параллельна СД МN – средняя линия трапеции MN параллельна АД и СД АС и ВД - диагонали трапеции Если АВ=СД, то трапеция ...Интеграл. Площадь криволинейной трапеции»
x. Различные виды криволинейных трапеций. Площадь криволинейной трапеции. Найти площадь криволинейной трапеции, ограниченной : графиком функции f(x) ...Интеграл. Площадь криволинейной трапеции
Цели и задачи урока: Обобщить и систематизировать теоретический материал по теме. Отработать навыки вычисления первообразных для функций. Отработать ...Длина окружности. Площадь круга. Практические применения
Цели развивающие: Активизировать деятельность учащихся через разнообразные виды самостоятельной работы. Способствовать развитию долговременной памяти ...Длина окружности. Площадь круга. Коллекция задач для 6 класса
. Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности примерно в раза больше ...Длина окружности. Площадь круга
Математический словарь:. Правильный многоугольник; Окружность, описанная около правильного многоугольника; Окружность, вписанная в правильный многоугольник; ...Длина окружности. Площадь круга
Устный счёт 500+310 :90 *60 -120 :14 910:13 *8 -80 :160 *350. Отрезки А В С К Круг Цилиндр Окружность Окружность, круг. В С А. Окружность - это замкнутая ...Деловая игра "Строитель"" к уроку математики по теме "Площадь многоугольника"
Цель урока:. усвоение учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции применение полученных знаний к решению практических ...Площадь прямоугольного треугольника
А В С D 12 дм 6 дм 12 · 6 = 72 (дм²) S□ = a · b S□ -? SΔ -? (12 · 6) : 2 = 36 (дм²) SΔ = (a · b ) : 2 Шаг 1. Шаг 1* (трудный). 10 дм 16 дм Шаг 2. ...Площадь трапеции
Игра «Угадай формулу». Площадь трапеции равна произведению полусуммы её оснований на высоту. H H1. Дано: ABCD – трапеция AD и BC основания, BH – высота ...Круг. Площадь круга
Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно ...Площадь треугольника
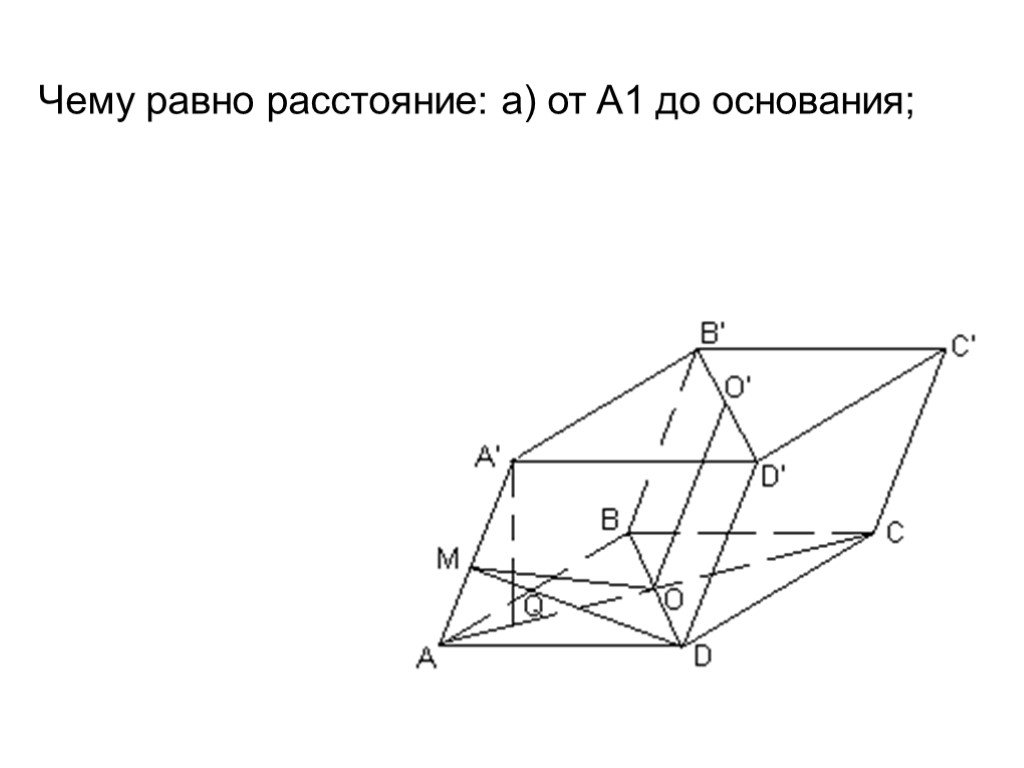
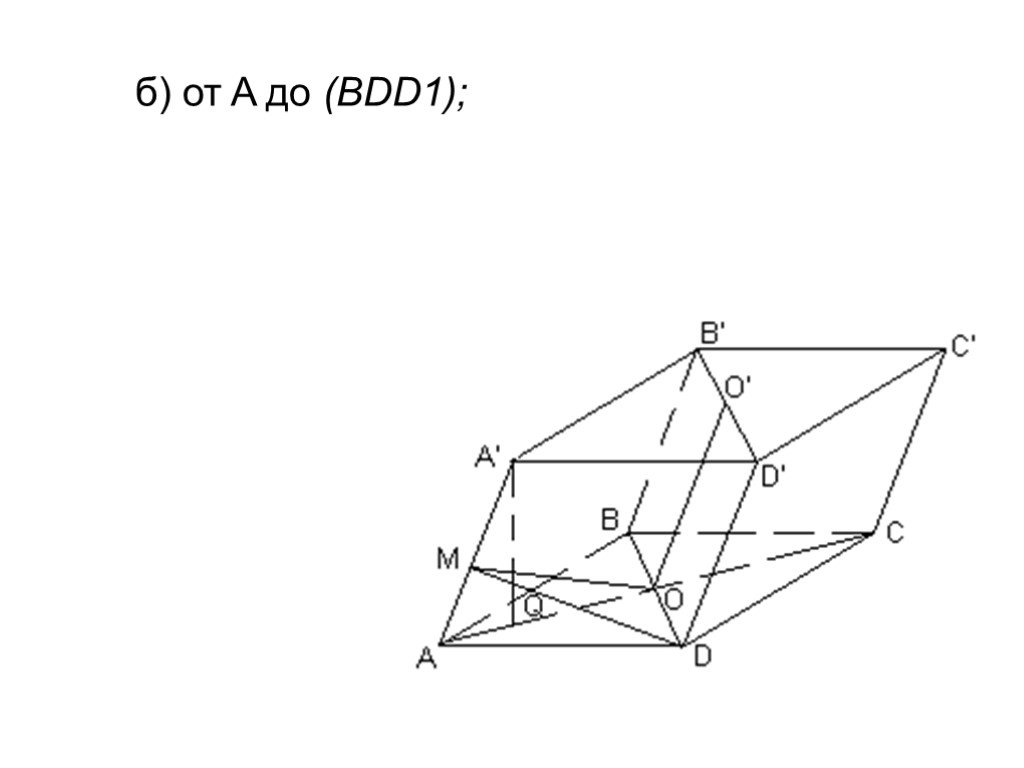
Устная работа. А В С D 6 см 10 см К. ABCD – параллелограмм. Найти площадь параллелограмма. 5 см 8 см. Теорема о площади треугольника. Дано: ABD – ...Объём наклонной призмы
Равные тела имеют равные объемы. Если тела А , В, С имеют равные размеры, то что можно сказать об объемах этих тел? Если тело разбито на части, являющиеся ...Конспекты
Площадь боковой поверхности цилиндра и конуса
Конспект урока по математике. Данные о преподавателе:. Кочерягина Галина Владимировна,. I. квалификационная категория,. . государственное ...Площадь поверхности прямоугольного параллелепипеда
Тема урока. . Площадь поверхности прямоугольного параллелепипеда. . . Базовый учебник. . Математика, 5 класс, Виленкин. . . . Цель ...Площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра. . . . . равна . , а диаметр основания — 8. Найдите высоту цилиндра. . Длина окружности основания ...Объем и площадь поверхности конических тел
Урок 4. Тема урока: «Объем и площадь поверхности конических тел». Тип учебного занятия:. изучение и первичное закрепление новых знаний и способов ...Площадь трапеции
План – конспект урока по геометрии с использованием ЭОР по теме «Площадь трапеции». Автор:. Макарова Татьяна Павловна,. учитель высшей категории ...Площадь прямоугольного треугольника
Конспект урока по математике. Тема: «Площадь прямоугольного треугольника». Тип урока:. изучение нового материала. Цель урока:. создать условия ...Площадь прямоугольника
Разработка урока-открытия по теме: «Площадь прямоугольника». учителя начальных классов, МАОУ «ГИМНАЗИЯ №1», г. Салехард,. . Кантарбаева Маргарита ...Длина окружности. Площадь круга. Сфера. Шар
Тема: Длина окружности. Площадь круга. Сфера. Шар. Цели урока:. 1. Познакомить учащихся с практическими способами измерения длины окружности и ...Площадь фигур. Единицы площади
Урок математики 3 класс. Кто работает с любовью, тот. вносит поэзию во всякую работу. Н.Г.Чернышевский. Тема урока:. Площадь фигур. Единицы ...Площадь треугольника
ПЛАН-КОНСПЕКТ УРОКА. Площадь треугольника__________________________________________. (Тема урока). . ФИО (полностью). . Ефимова Светлана ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 апреля 2019
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию