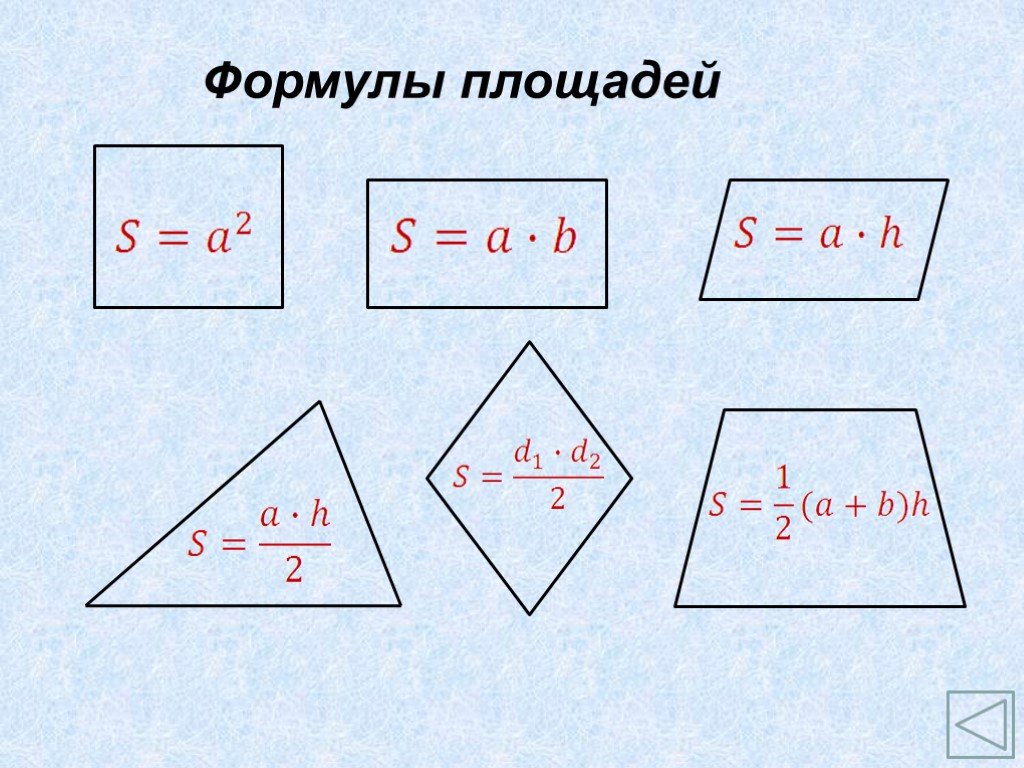
Презентация "Площадь параллелограмма, треугольника, трапеции" по математике – проект, доклад
Слайд 1
Слайд 2
Слайд 3
Слайд 4
Слайд 5
Слайд 6
Слайд 7
Слайд 8
Слайд 9
Слайд 10
Слайд 11
Слайд 12
Слайд 13
Слайд 14
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19
Слайд 20Презентацию на тему "Площадь параллелограмма, треугольника, трапеции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
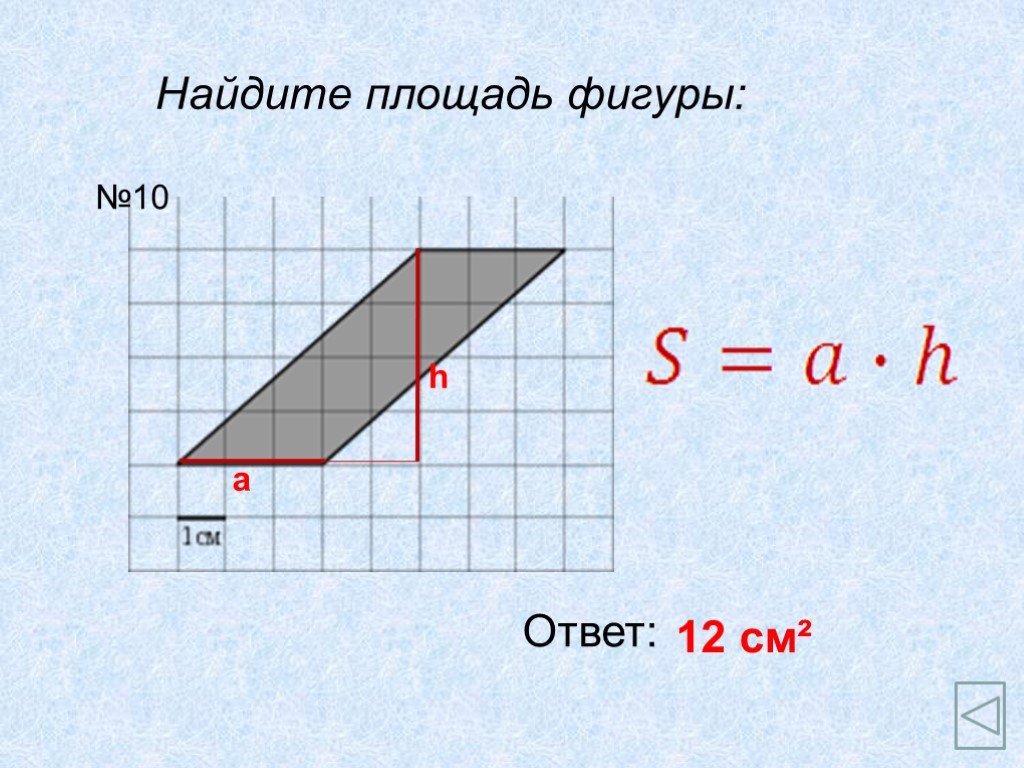
Площадь параллелограмма
Ход урока: Проверка домашнего задания. Решение упражнений. Устные упражнения. Самостоятельная работа. Итог урока. Домашнее задание. Задача 1. 150° ...
Площадь параллелограмма
Свойства площадей. 10. Равные многоугольники имеют равные площади. 20. Если многоугольник составлен из нескольких многоугольников, то его площадь ...
Площадь параллелограмма
Цели урока. дать определение высоты параллелограмма ; доказать теорему о площади параллелограмма; показать применение формулы в процессе решения задач. ...
Площадь параллелограмма
Пример 1. Стороны параллелограмма равны 15 см и 9 см. Высота, опущенная на первую сторону, равна 6 см. Найдите высоту, опущенную на вторую сторону ...
Площадь криволинейной трапеции
Вычислить площадь криволинейной трапеции. ...
Площадь криволинейной трапеции и интеграл
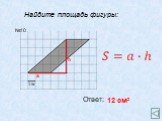
Криволинейная трапеция. Отрезок [a;b] называют основанием этой криволинейной трапеции. Криволинейной трапецией называется фигура, ограниченная графиком ...
Площадь квадрата, прямоугольника, параллелограмма
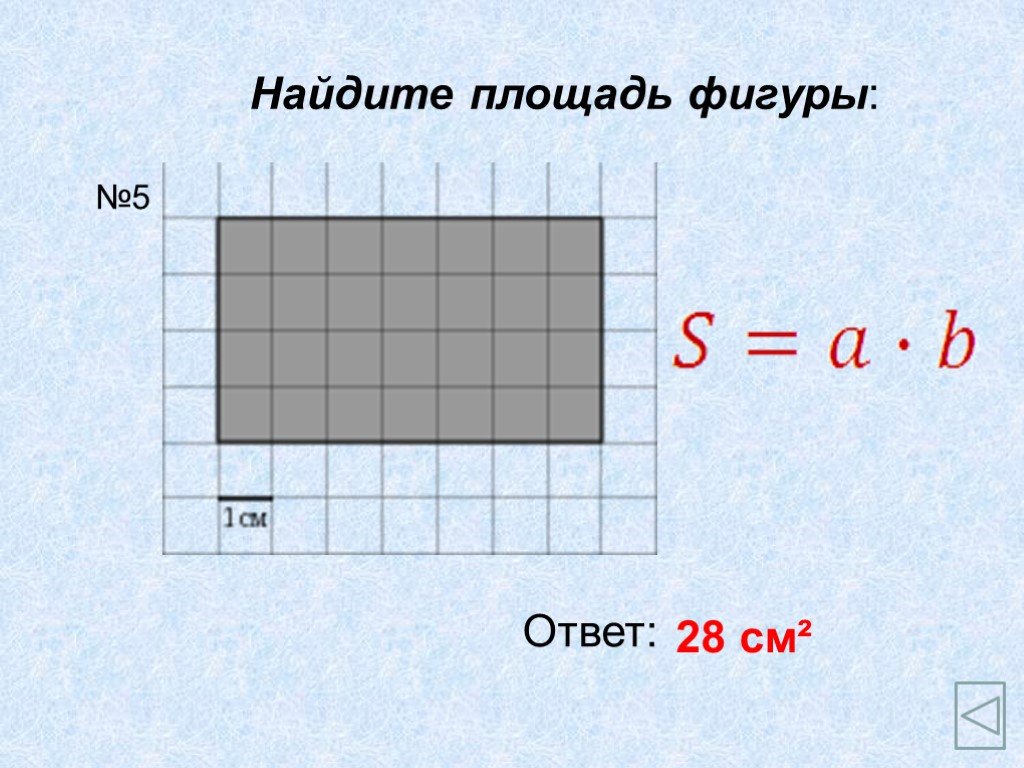
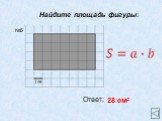
Площадь квадрата. Площадь квадрата со стороной а равна а2. Площадь квадрата. Задача. Найти сторону квадрата, если его площадь равна 16 см2. Площадь ...
Площадь криволинейной трапеции
Площадь криволинейной трапеции. y x B C D A a b Y = f(x) s. ABCD –криволинейная трапеция. S = F(b) – F(a) F/ (x) = f(x). Y=g(x). Записать формулу ...
Площадь треугольника
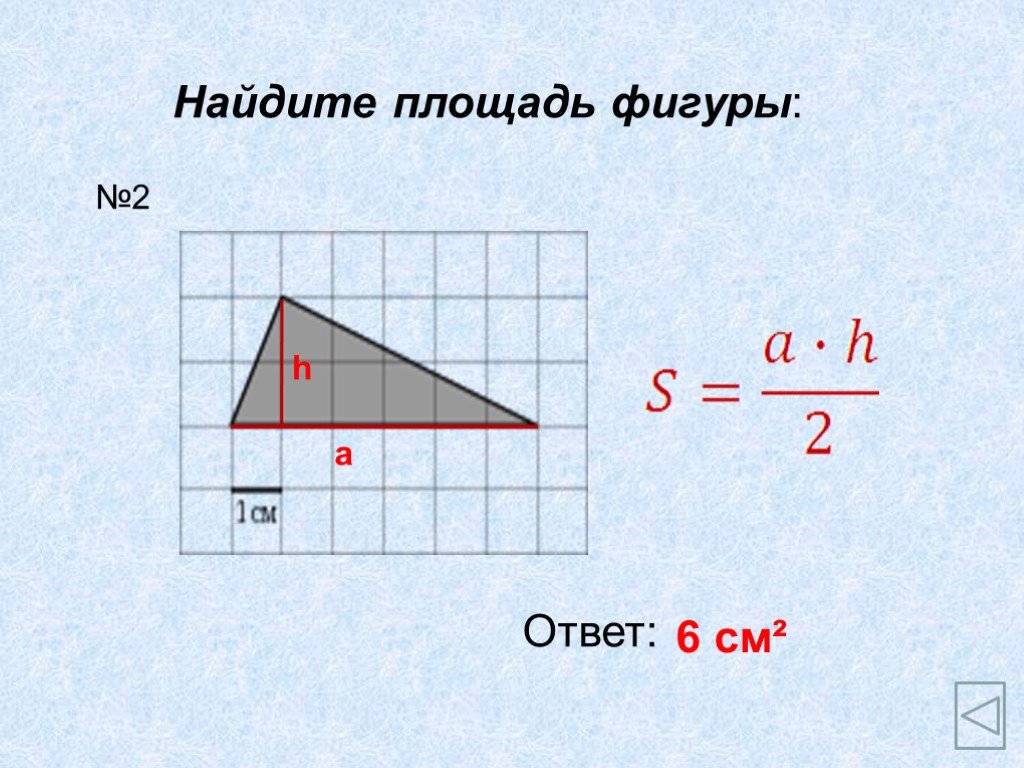
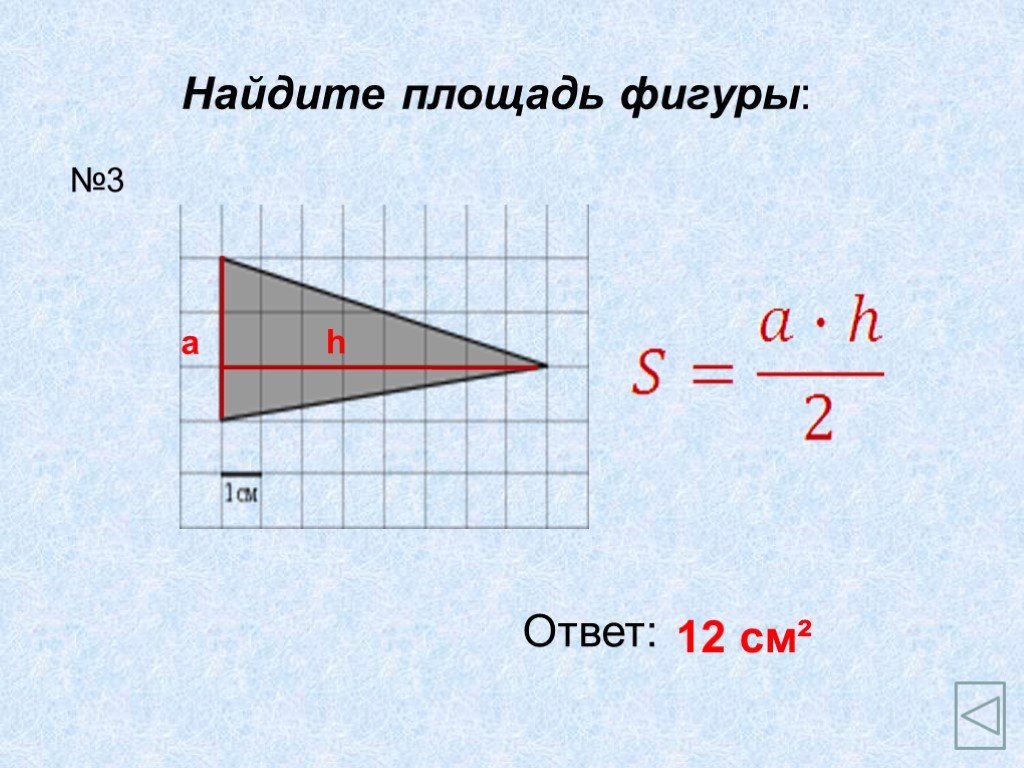
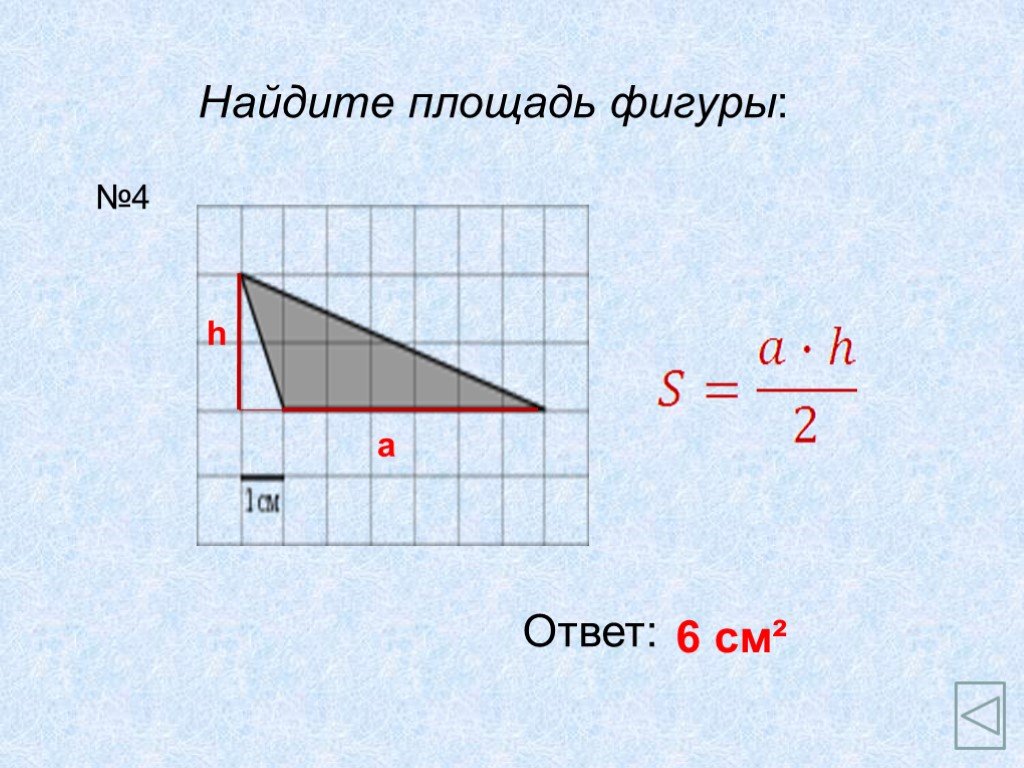
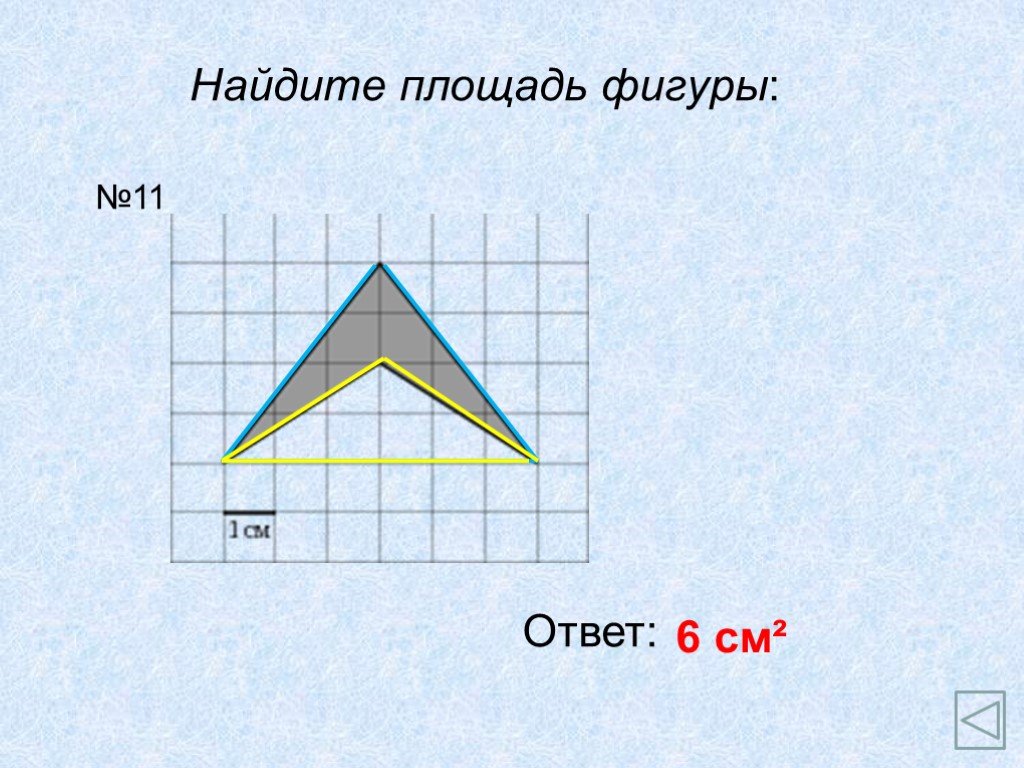
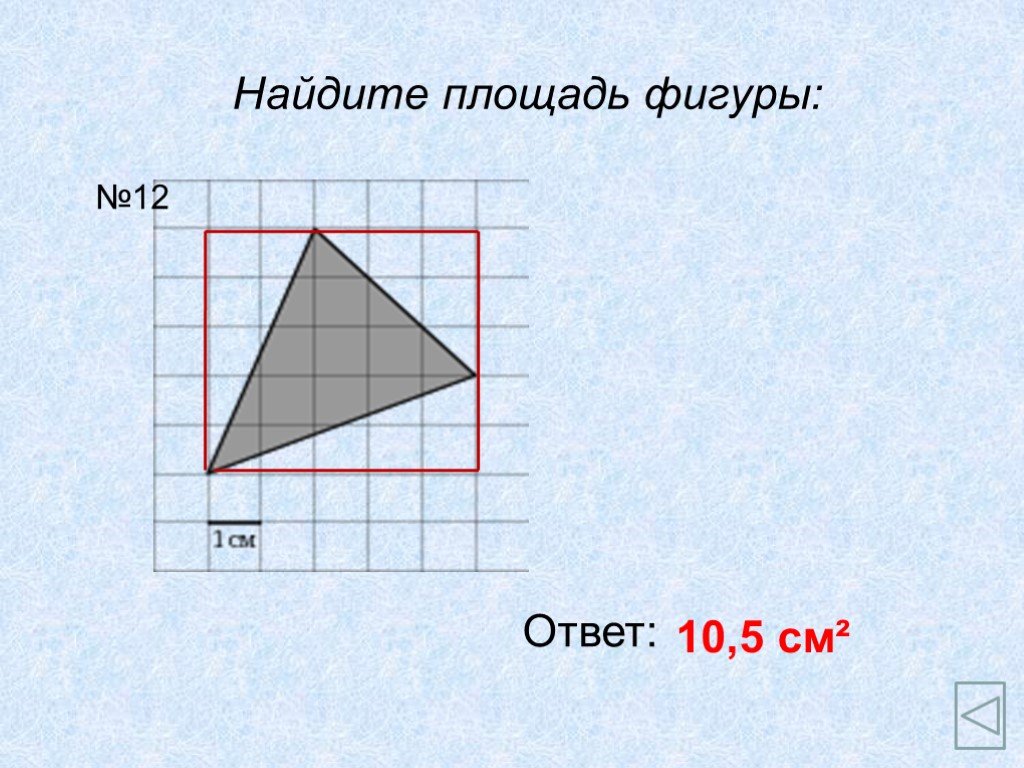
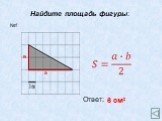
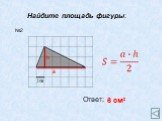
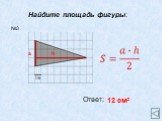
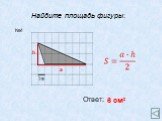
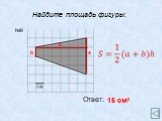
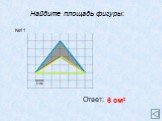
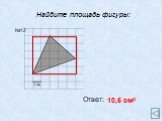
АС- основание ВН- высота; ВС- основание АН1- высота. Теорема. Площадь треугольника равна половине произведения его основания на высоту. Док-во: АВС= ...
Площадь: площадь трапеции
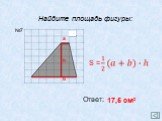
Определение трапеции:. В А С D. АD // ВС, АВ и СD – непараллельные отрезки. Трапецией называется четырёхугольник, у которого только две противолежащие ...
Площадь треугольника. Полезные теоремы, следствия и задачи
Вспомните ответы на вопросы. 1) Сформулируй понятие площади геометрической фигуры. 2) Сформулируй основные свойства площадей геометрических фигур. ...
Площадь треугольника
Площадь треугольника. Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Основания и высоты треугольника. ...
Площадь треугольника
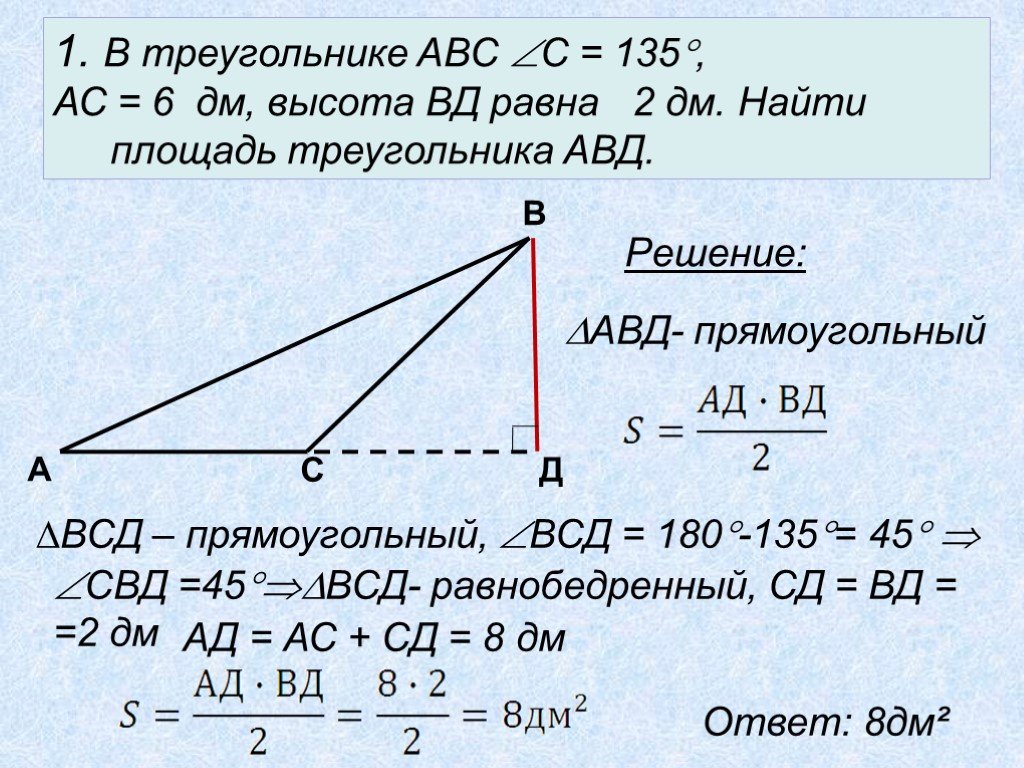
Устная работа. А В С D 6 см 10 см К. ABCD – параллелограмм. Найти площадь параллелограмма. 5 см 8 см. Теорема о площади треугольника. Дано: ABD – ...
Площадь треугольника
Человек, вооруженный знаниями способен решить любые задачи. Свойства площадей. Равные многоугольники имеют равные площади. F = H S1 = S2 S1 S2. ...
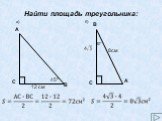
Площадь треугольника
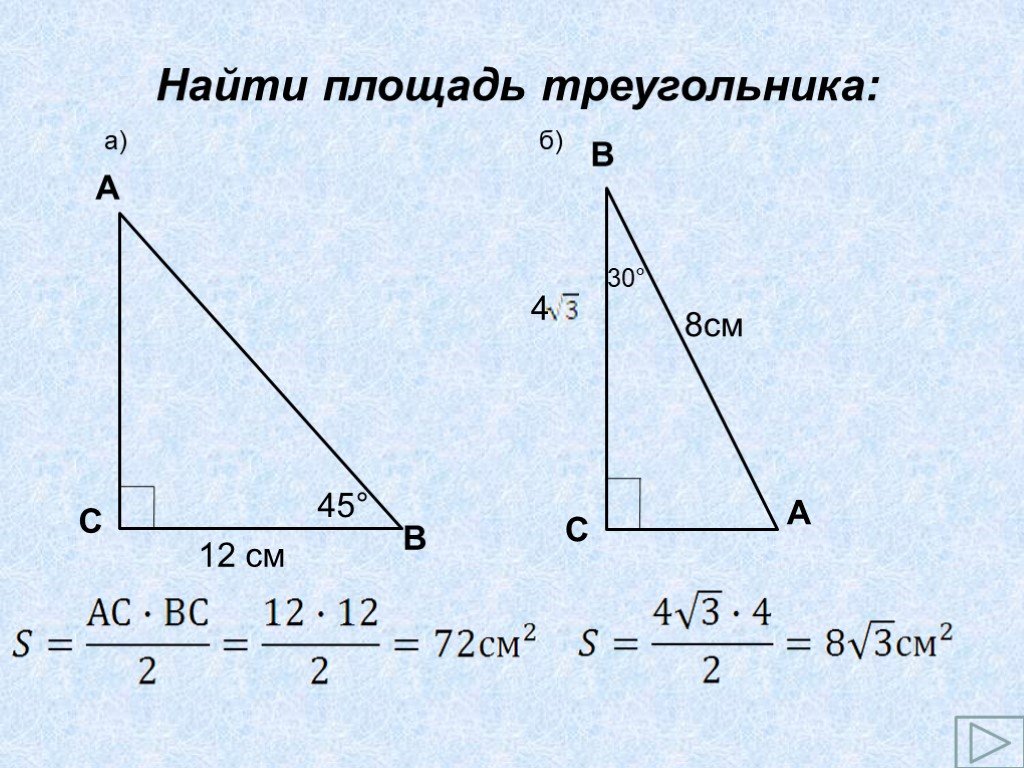
Найти площади треугольников:. У Х А В О Н 60° 6 4. ДАНО: ∆АВО: ВО = а, АО =b, ∟С=α Найти площадь треугольника. ВН - аsinα. SABC=½АО∙ВН= ½ а ∙b ∙ sinα. ...
Площадь трапеции
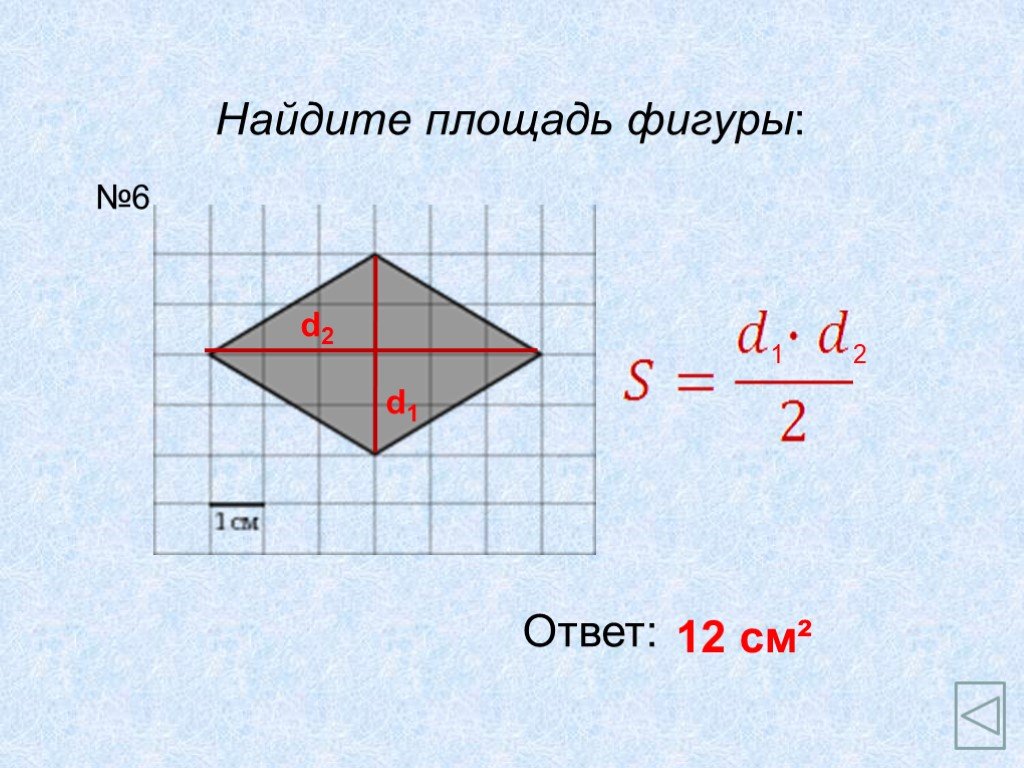
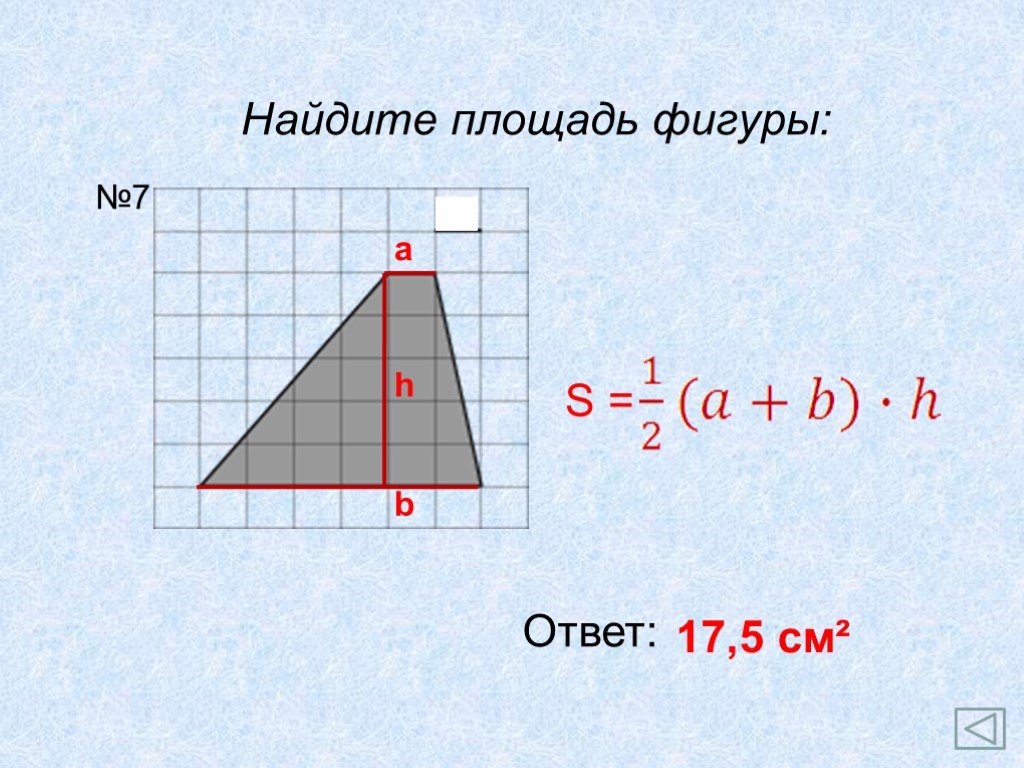
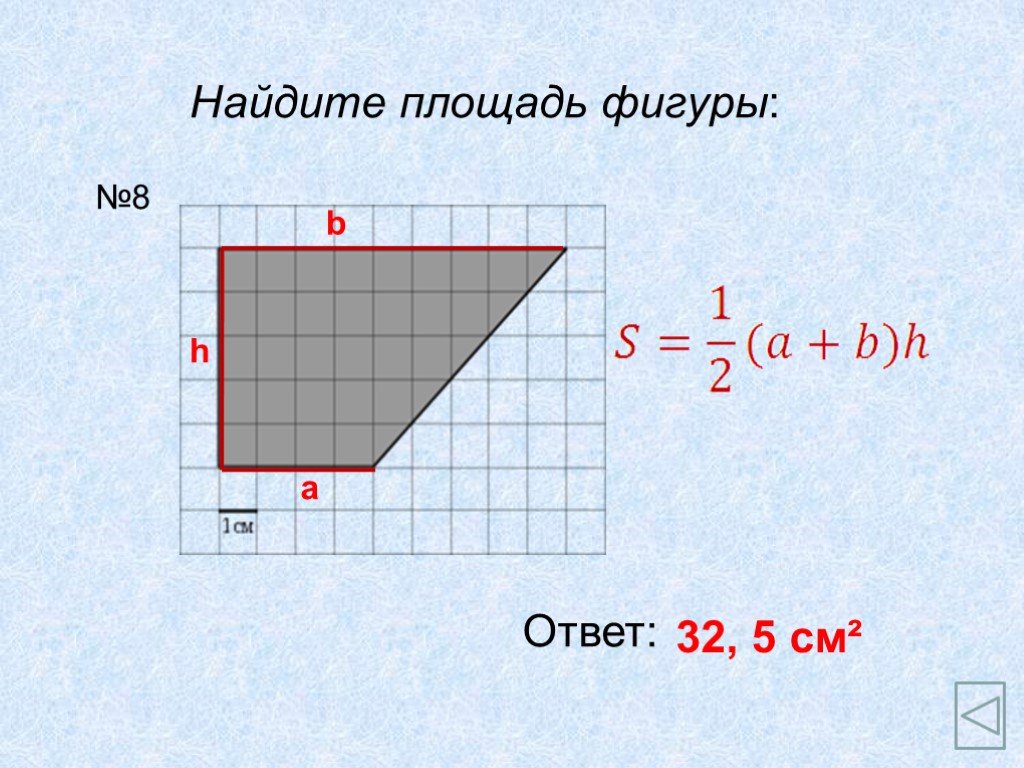
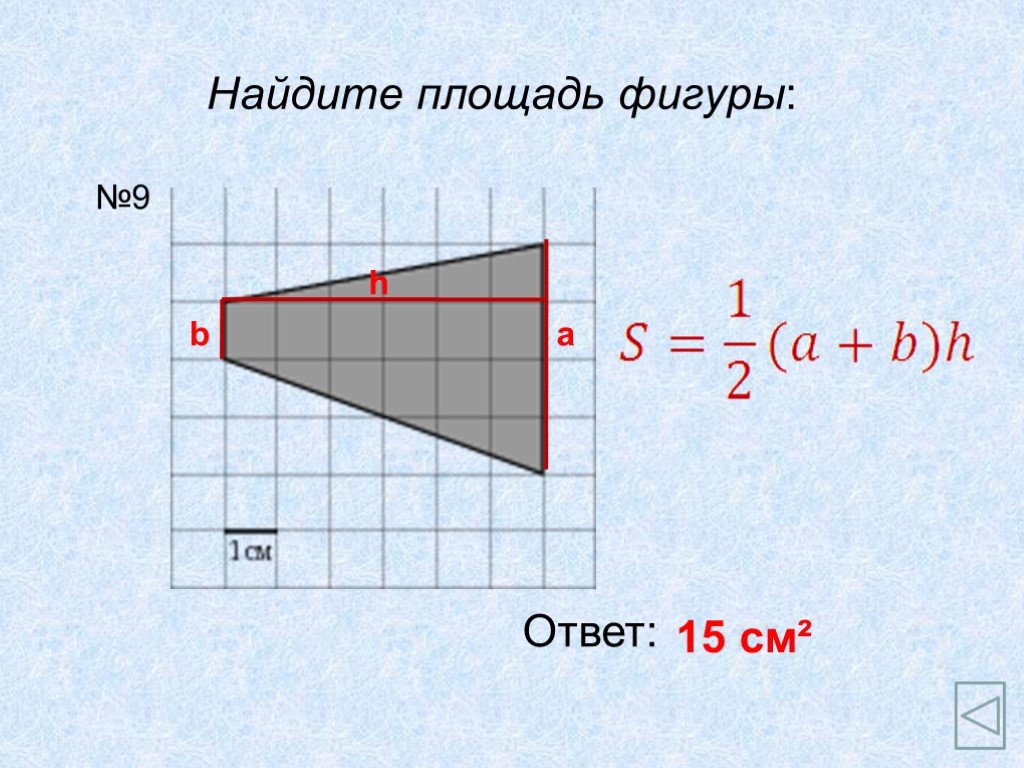
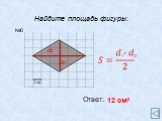
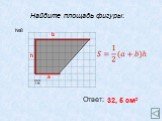
Площадь трапеции 8 класс. Трапеция и её элементы:. А В С D H О a b c d d1 d2. Свойства: Площадь фигуры равна сумме площадей ее частей 2.Высота трапеции ...
Интеграл. Площадь криволинейной трапеции»
x. Различные виды криволинейных трапеций. Площадь криволинейной трапеции. Найти площадь криволинейной трапеции, ограниченной : графиком функции f(x) ...
Интеграл. Площадь криволинейной трапеции
Цели и задачи урока: Обобщить и систематизировать теоретический материал по теме. Отработать навыки вычисления первообразных для функций. Отработать ...
Площадь трапеции
Трапеция. ВС параллельна АД, АВ не параллельна СД МN – средняя линия трапеции MN параллельна АД и СД АС и ВД - диагонали трапеции Если АВ=СД, то трапеция ...
Площадь трапеции
А В С D a b h. 8 5 О х 12 h = 8. Домашнее задание Вопросы 1 – 6. Задачи № 37, 40. ...Конспекты
Площадь параллелограмма, трапеции, треугольника
Тема урока: Площадь. параллелограмма, трапеции, треугольника. Тип урока:. Урок обобщения и систематизации знаний. . Цели урока:. . Закрепление ...
Площадь прямоугольного треугольника
Муниципальное бюджетное общеобразовательное учреждение. гимназия №19 имени Поповичевой Н.З. г. Липецка. Конспект урока по ...
Площадь прямоугольного треугольника
Муниципальное общеобразовательное учреждение гимназия № 10. Урок по математике УМК “Школа 2100” 4 класс. «Площадь прямоугольного треугольника». ...
Площадь прямоугольного треугольника
Урок математики. . по теме. "Площадь прямоугольного треугольника". Основные цели:. 1) Сформировать представление о прямоугольном треугольнике, ...
Площадь прямоугольного треугольника
Конспект урока по математике. Тема: «Площадь прямоугольного треугольника». Тип урока:. изучение нового материала. Цель урока:. создать условия ...
Площадь треугольника. Решение задач
геометрия. . 8 класс. . Урок «Площадь треугольника. Решение задач». Оборудование:. 1. ноутбук, проектор. 2. учебники геометрия 7-9 Атанасян. ...
Синус, косинус, тангенс. Площадь треугольника
Автор: Чичерова Татьяна Ивановна. Место работы: МОУ «Образцовская СОШ». Должность: учитель математики. . . Урок геометрии в 9 классе. Тема: ...
Площадь треугольника
ПЛАН-КОНСПЕКТ УРОКА. Площадь треугольника__________________________________________. (Тема урока). . ФИО (полностью). . Ефимова Светлана ...
Площадь треугольника
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №3 г.Козьмодемьянска». . Республики Марий Эл. ...
Площадь треугольника
Урок геометрии в 8 классе. «Площадь треугольника». Цель урока:. создать условия для вывода формулы площади прямоугольного и произвольного ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 мая 2019
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию
