Презентация "Понятие пирамиды" по математике – проект, доклад
Презентацию на тему "Понятие пирамиды" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Процент. Понятие, определение, решение задач
ЗУН. Знать и уметь находить: Что называют «Процентом»; Правила нахождения: дроби от числа, числа по значению дроби и нахождения части от числа; Правила ...Понятие угла
Готовимся к ОГЭ Вычислите:. В А. Угол поворота АОВ соответствует длине пути, пройденного точкой В от начального положения А Если подвижный вектор ...Понятие центральной симметрии
Содержание:. Определение Доказательство Применение в жизни Применение в природе Решение задачи. Преобразование, переводящее каждую точку А фигуры ...Понятие предела функции
Определение. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0. ...Понятие процента
ГЕНА! Я подсчитал, что старуха Шапокляк в феврале подстроила нам 19 пакостей, в марте 20, а в апреле 18. Интересно, в каком месяце она была самой ...Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Понятие осевой симметрии
Определение и теорема. Примеры Задачи. Осевой симметрией с осью a называется такое отображение пространства на себя , при котором любая точка М переходит ...Определение призмы, пирамиды
Пусть даны две параллельные плоскости и β. Построим в плоскости произвольный n-угольник A1A2…An. A1 A3 An An-1 β B1 B3 Bn Bn-1. Через его вершины ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Объём пирамиды
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...Объем пирамиды
Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...Объем пирамиды
Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...Загадка пирамиды
I Вступление II. Из истории. 1. Пирамида Джосера 2. Пирамида Хеопса III. Об Александре Голоде IV. Пирамида и архитектура 1. Исследования и практическое ...Египетские пирамиды
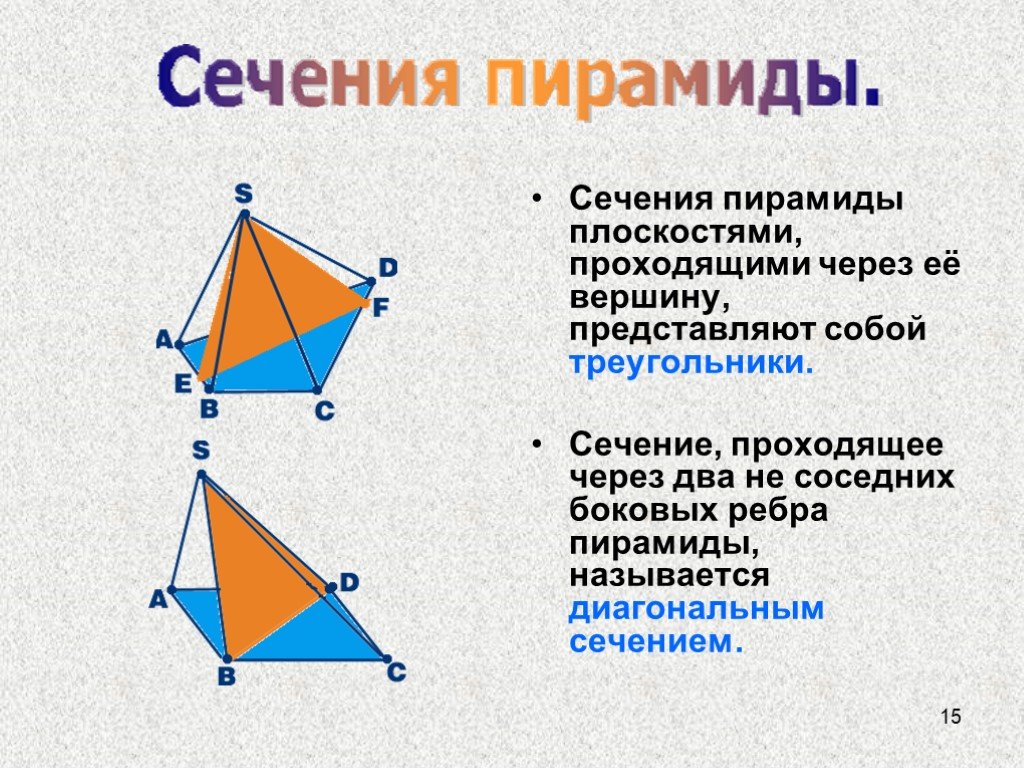
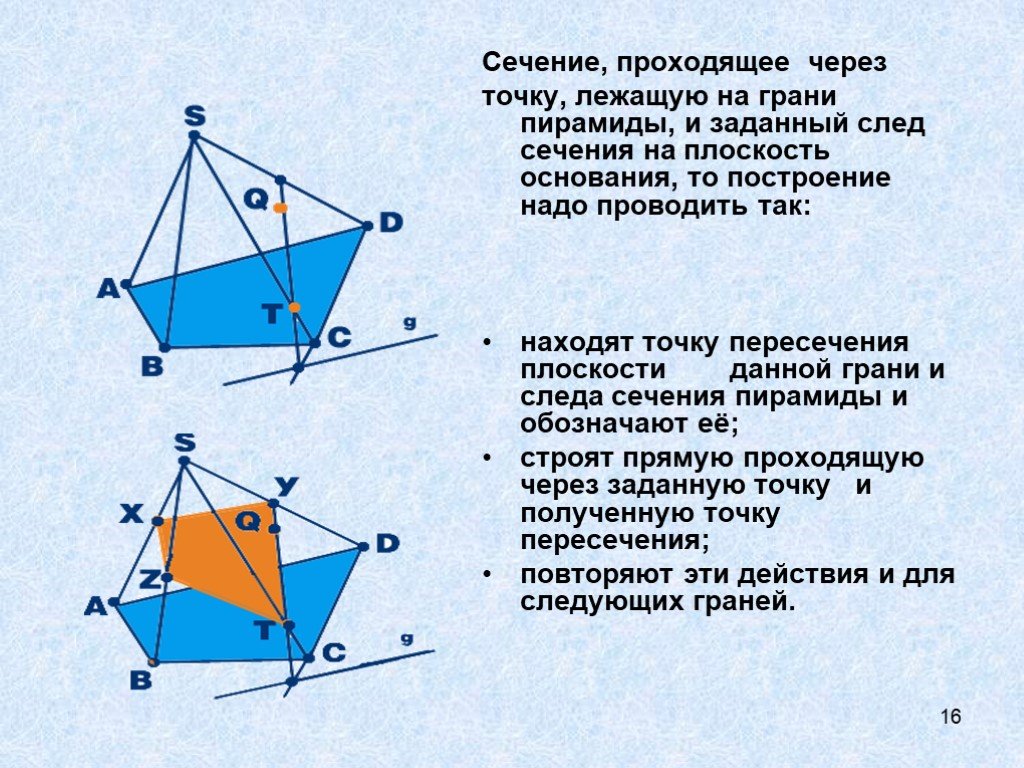
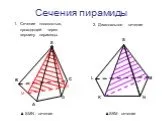
Почему Египетские пирамиды называют немым трактатом по геометрии? Автор: Зеленцов Роман 10а класс. МОУ СОШ с.Становое. 2008 год. Цель: научиться определять ...Сечения пирамиды
3. Сечение пирамиды плоскостью с заданным следом. A B C F P Q MNPQ - сечение. 4. Сечение пирамиды плоскостью, параллельной основанию. MNKP - сечение ...Пирамида. Сечения пирамиды
. Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD. Построить линейный угол двугранного угла, образованного плоскостью ...Десятичные дроби. Понятие десятичной дроби
Немного истории. Дроби, как известно, возникли в связи с делением предметов на несколько частей. При решении разных практических задач возникали дроби ...Понятие абсолютного показателя. Виды абсолютных показателей
Относительные показатели, их роль и типология. Относительные показатели - это цифровые обобщающие показатели, которые есть результат сопоставления ...Понятие одночлена стандартный вид одночлена
Определение: Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, ...Понятие алгебраической дроби
Алгебраическая сумма. Алгебраическая сумма – это запись, состоящая из нескольких алгебраических выражений, соединенных знаком «+» или «-». Найдите ...Конспекты
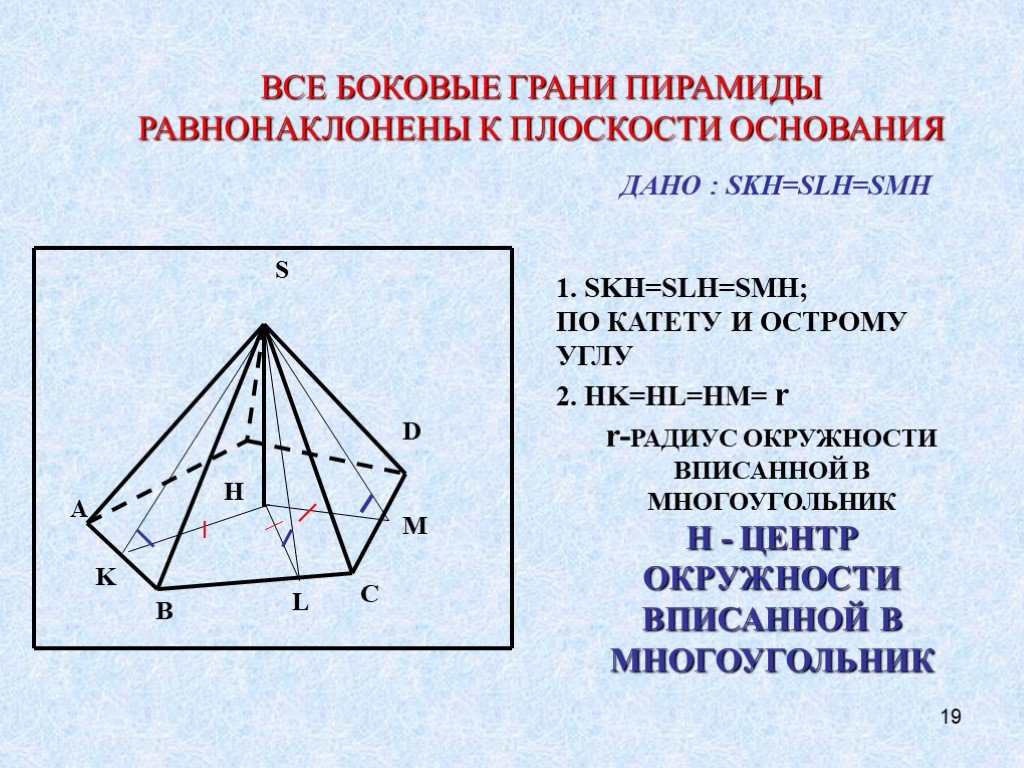
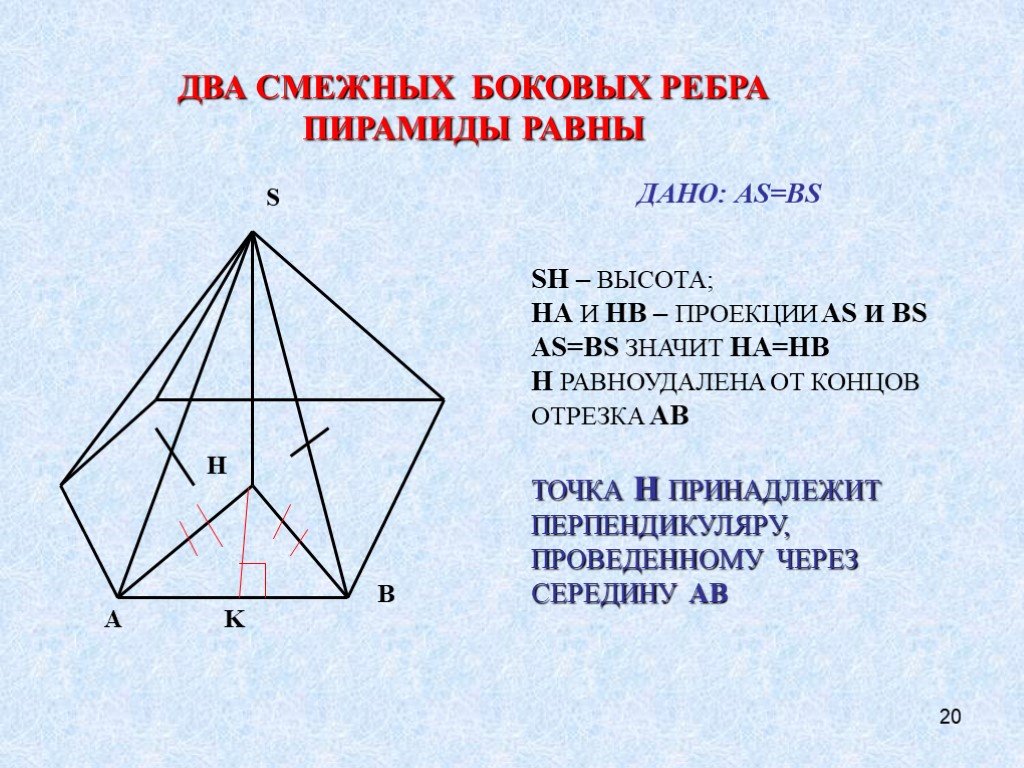
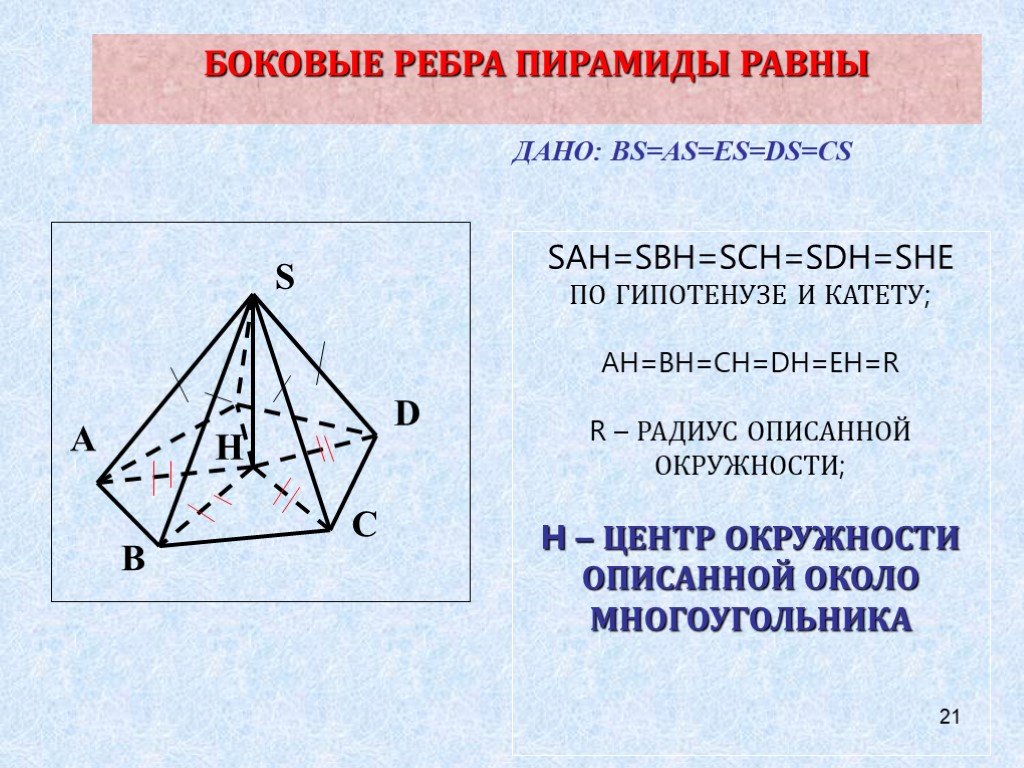
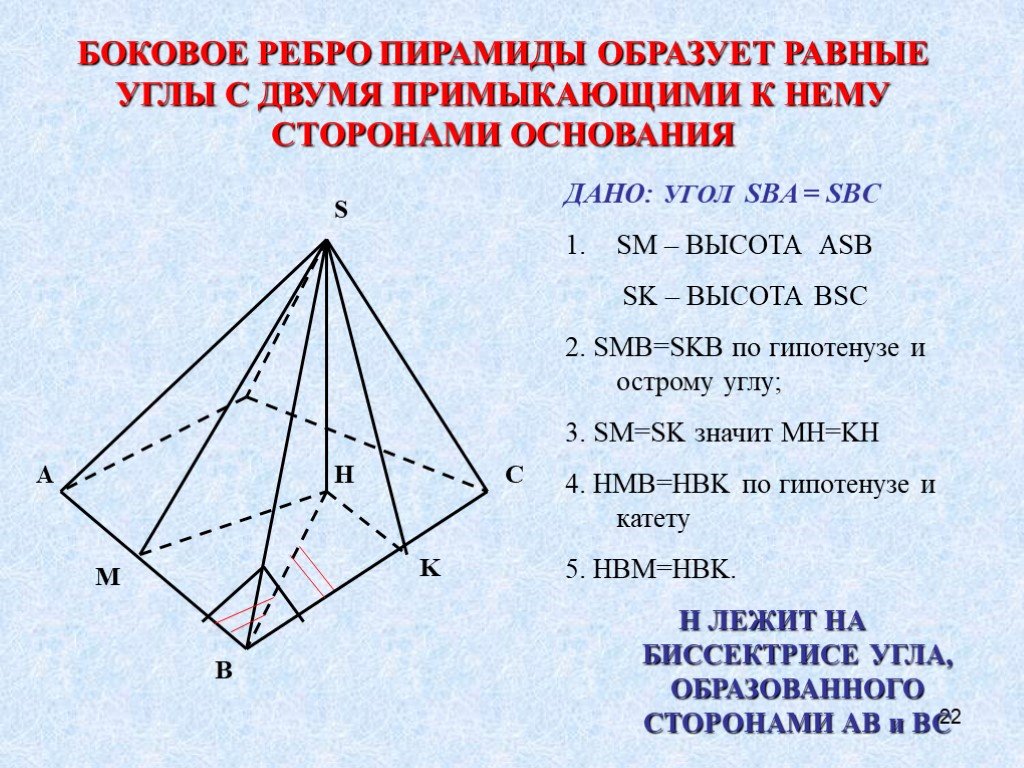
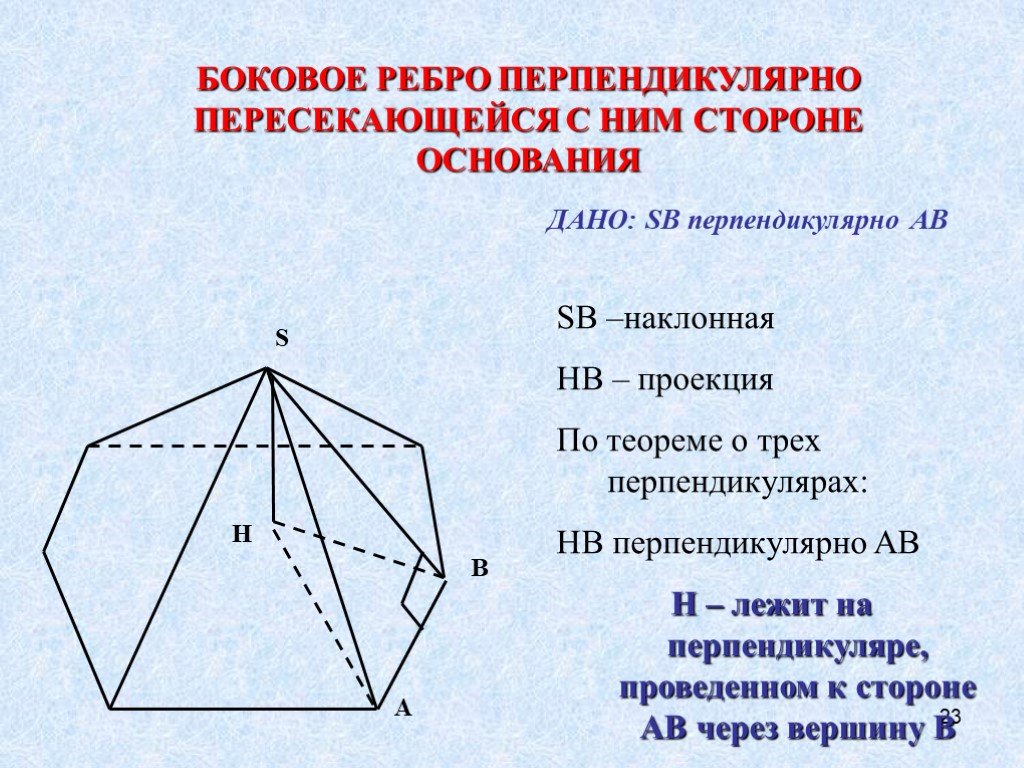
Проекция вершины пирамиды на плоскость основания
Метод проектов. . Проекция вершины пирамиды на плоскость основания. Тип:. исследовательский. Учебный предмет:. геометрия. Участники:. 10 класс. ...Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице
Тема:. Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице. 5 класс специальной (коррекционной) школы. Цели:. . . Познакомить ...Понятие процента
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА. . Юрисарова Юлия Григорьевна. ,. . учитель математики. . МКОУ «Лицей» г.Калачинска Омской области. Предмет ...Понятие степени с любым рациональным показателем
ПЛАН-КОНСПЕКТ УРОКА. . «Понятие степени с любым рациональным показателем» . ФИО. . . Грудинина Мария Михайловна. . . . Место ...Понятие о скорости. Задачи на нахождение скорости движения
План-конспект урока по математике (4класс). Учитель Ленинской Ош красногвардейского района Республики Крым. Тема. : Понятие о скорости. Задачи ...Понятие первообразной
Схема конспекта урока. Аттестуемый педагог Резниченко Дарья Анатольевна. Предмет. математика. 11 «Б» класс Тема урока: «Понятие первообразной». ...Понятие вероятности. Подсчёт вероятности
ПЛАН-КОНСПЕКТ УРОКА. . «Понятие вероятности. Подсчёт вероятности» Цель урока: Организация деятельности учащихся по формированию понятия вероятности, ...Понятие о проценте
Доброхотова Эльмира Рафаилевна. Учитель математики. . МБОУ «Средняя общеобразовательная школа №9». . г Чистополя. План-конспект урока. ...Понятие вектора
Учитель математики - Юшина Раиса Алексеевна. . МБОУ СОШ № 18. . . Тема:. 9КЛ. . 2010. год. Тема:. Понятие ...Понятие вектора
Муниципальное общеобразовательное учреждение. «Завьяловская средняя общеобразовательная школа №1». Завьяловского района Алтайского края. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 декабря 2018
Категория:Математика
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию