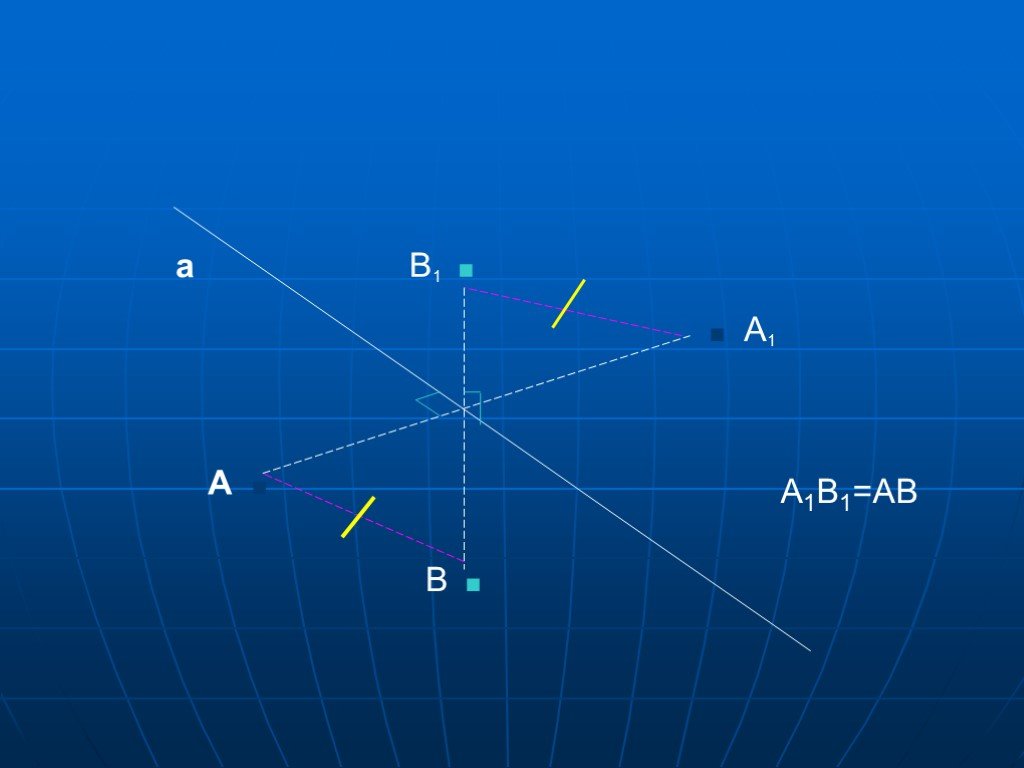
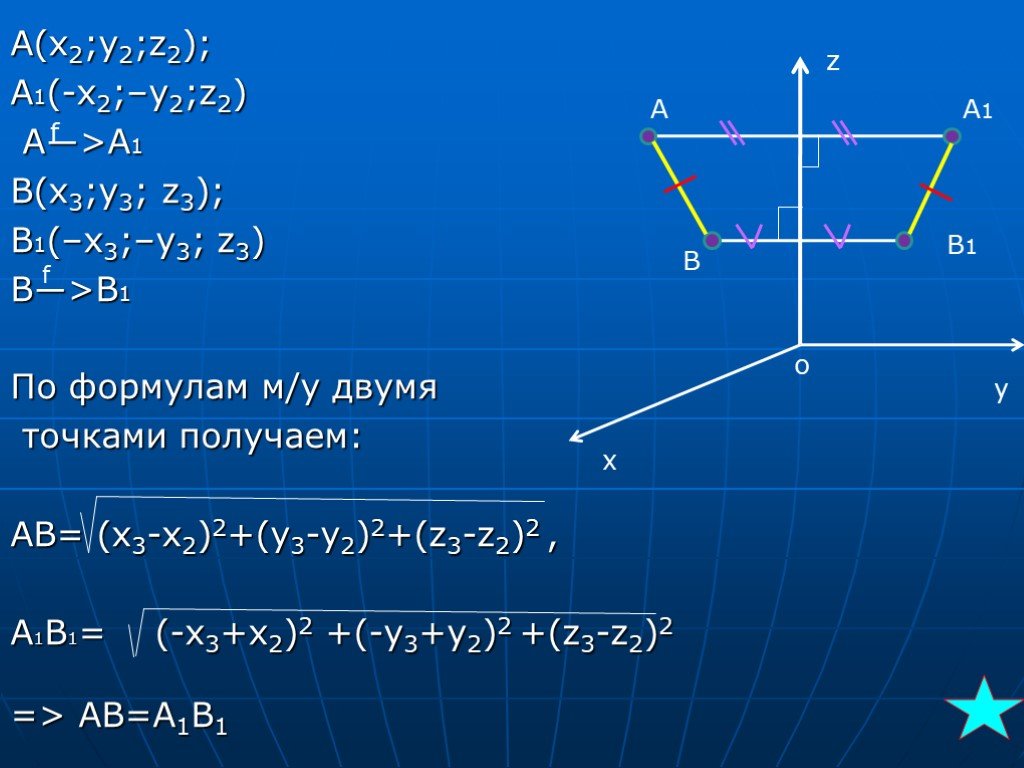
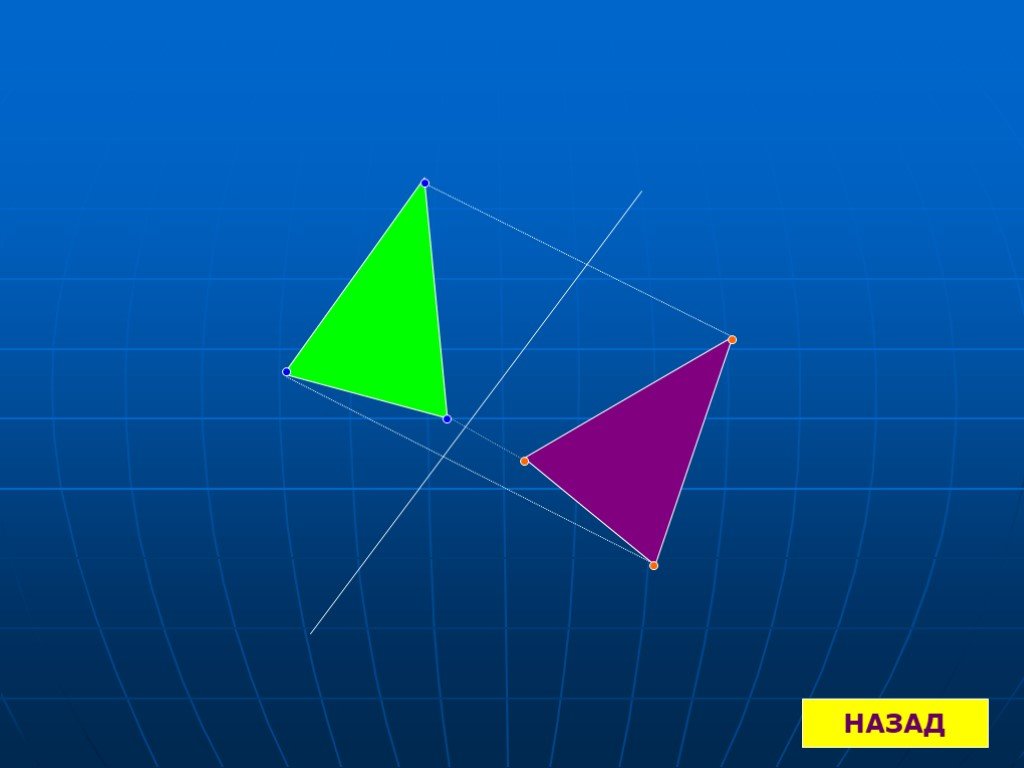
Презентация "Понятие осевой симметрии" по математике – проект, доклад
Презентацию на тему "Понятие осевой симметрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Понятие центральной симметрии
Содержание:. Определение Доказательство Применение в жизни Применение в природе Решение задачи. Преобразование, переводящее каждую точку А фигуры ...Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника
Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранника. Задачи урока: Ввести понятие правильного многогранника, ...Понятие функции
Содержание:. что такое функция история создания названия функции аналитический способ задания функции табличный способ задания функции способ описания ...Группы симметрии фигур
Немного теории. Фигуру называют центрально-симметричной, а точку О – ее центром симметрии, если преобразованием симметрии относительно точки о фигура ...Понятие производной функции
Автор Сизова Н. В., г. Саров. Производная. Историческая справка. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики ...Понятие степени. Свойства степени. Преобразование степеней
Понятие степени с натуральным показателем. Свойства степени с натуральным показателем. Степень с целым и дробным показателем. Понятие корня. Преобразования ...Понятие одночлена стандартный вид одночлена
Определение: Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, ...Понятие площади и объёма
Цель урока.Обобщение и систематизация знаний понятия площади и объёма. Отработка навыков умения переводить одни единицы измерения в другие. Применение ...
Мир симметрии
Введение. С симметрией мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже ...Понятие о производной функции
Цели урока:. ОБУЧАЮЩАЯ : 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический смысл производной; 2) ...Красота и гармония в симметрии
Цели:. Научиться распознавать виды симметрии Найти симметричные фигуры вокруг нас Исследовать симметричные фигуры и показать их красоту. Я в листочке, ...Мир наш полон симметрии
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...История симметрии
Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей ...История изучения симметрии в природе
Оглавление: Введение………………………………………………………………………….2 Глава 1. Симметрия в точных науках………………………………………..3 1.1. Геометрия…………………………………………………………………….4 ...Десятичные дроби. Понятие десятичной дроби
Немного истории. Дроби, как известно, возникли в связи с делением предметов на несколько частей. При решении разных практических задач возникали дроби ...Типы симметрии
О ПРОЕКТЕ. Тема: Мир симметрии и симметрия мира Автор работы: Скакалин Андрей, 6 класс Руководитель проекта: Столбова Лидия Викторовна, учитель математики ...Общие понятия о симметрии. Элементы симметрии
План. Введение Термин симметрии Элементы симметрии. Введение. При обработке металла под давлением мы имеем дело с поликристаллами. Одним из важных ...Виды симметрии
Определение. В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, ...Осевая и центральная симметрии
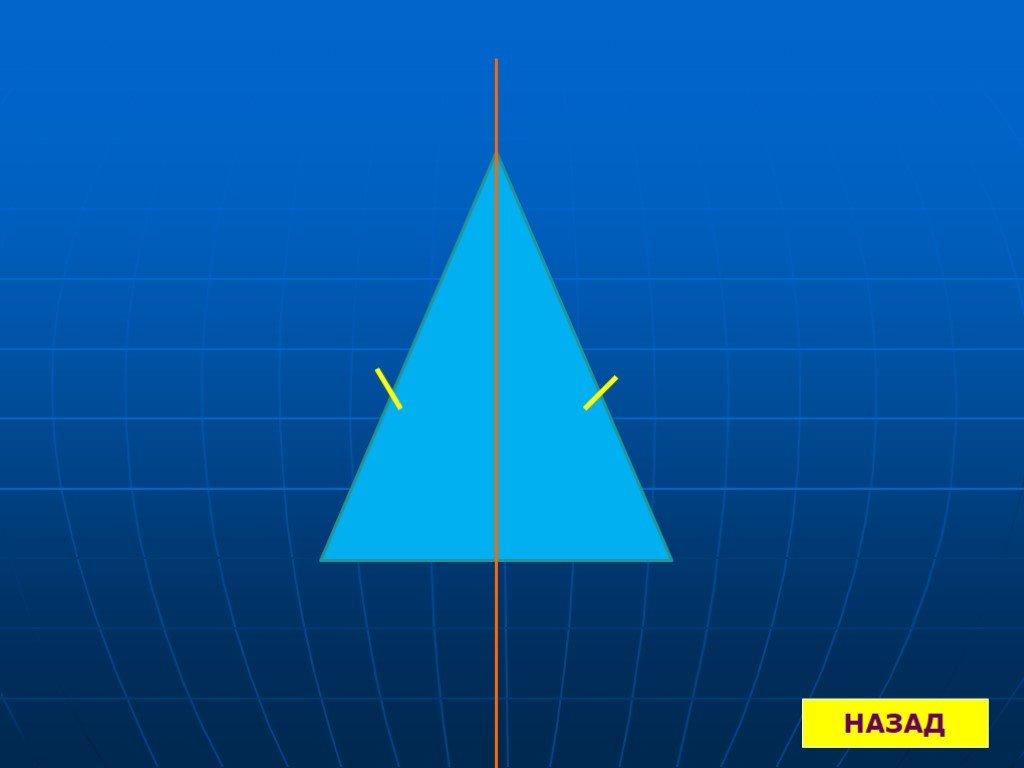
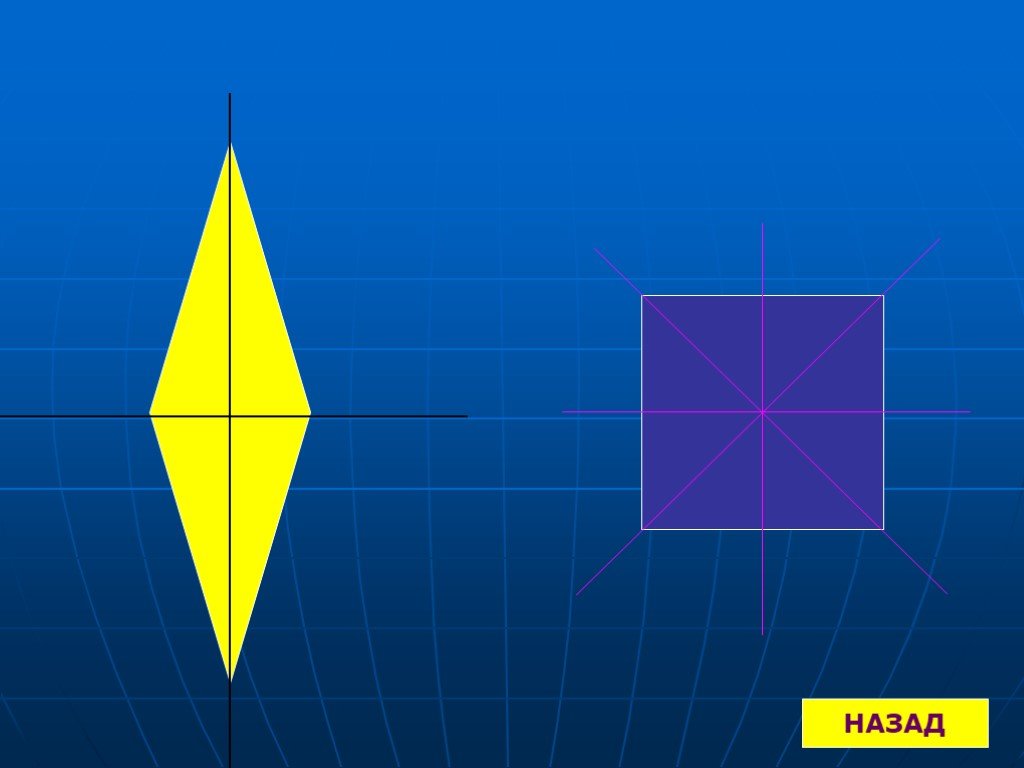
Что такое симметрия? Осевая симметрия. Построение осевой симметрии. Ценральная симметрия. Построение центральной симметрии. Симметрия в окружающем ...Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Конспекты
Понятие степени с любым рациональным показателем
ПЛАН-КОНСПЕКТ УРОКА. . «Понятие степени с любым рациональным показателем» . ФИО. . . Грудинина Мария Михайловна. . . . Место ...Симметрия. Виды симметрии
. Урок для 8 класса на тему «Симметрия. Виды симметрии». Содержание. . ...Понятие первообразной
Схема конспекта урока. Аттестуемый педагог Резниченко Дарья Анатольевна. Предмет. математика. 11 «Б» класс Тема урока: «Понятие первообразной». ...Понятие процента
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА. . Юрисарова Юлия Григорьевна. ,. . учитель математики. . МКОУ «Лицей» г.Калачинска Омской области. Предмет ...Понятие о проценте
Доброхотова Эльмира Рафаилевна. Учитель математики. . МБОУ «Средняя общеобразовательная школа №9». . г Чистополя. План-конспект урока. ...Понятие о скорости. Задачи на нахождение скорости движения
План-конспект урока по математике (4класс). Учитель Ленинской Ош красногвардейского района Республики Крым. Тема. : Понятие о скорости. Задачи ...Понятие вектора
Учитель математики - Юшина Раиса Алексеевна. . МБОУ СОШ № 18. . . Тема:. 9КЛ. . 2010. год. Тема:. Понятие ...Понятие о многоугольнике
Муниципальное общеобразовательное учреждение. «Дубовская СОШ с углубленным изучением отдельных предметов». Белгородского района Белгородской области. ...Оси симметрии
МКОУ СОШ. . с. Ивановка. Открытый урок в 1 классе. «Ось симметрии». Тукало С.А. Тема урока:. Ось симметрии. Цель урока:. ...Понятие арккосинуса. Уравнение вида сosх = а
Разработчик материала:. . Матвеева Мария Викторовна. учитель математики. ГБОУ ШИ «Олимпийский резерв». Программированный урок для 10 класса ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 августа 2019
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию