Презентация "Мир наш полон симметрии" (8 класс) по математике – проект, доклад
Презентацию на тему "Мир наш полон симметрии" (8 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Мир симметрии
Введение. С симметрией мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже ...Симметрия. Осевая и центральная симметрии
Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность». Симметрия является той идеей, с помощью ...Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника
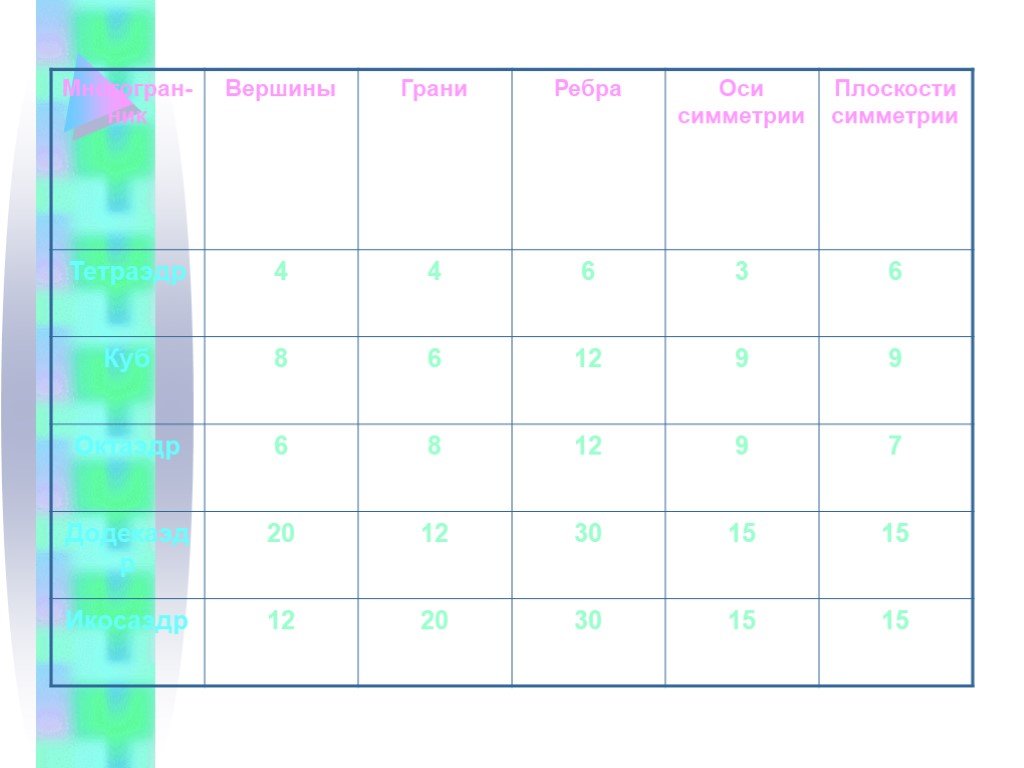
Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранника. Задачи урока: Ввести понятие правильного многогранника, ...Примеры симметрии в природе
В современном понимании симметрия — это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии ...Понятие центральной симметрии
Содержание:. Определение Доказательство Применение в жизни Применение в природе Решение задачи. Преобразование, переводящее каждую точку А фигуры ...Осевая и центральная симметрии
«Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает оттого, что в нем соблюдены правила и мера». Ф.Блондель. ...Осевая и центральная симметрии
Симметрия растений. Симметрия в животном мире. Симметрия в архитектуре. Примеры симметрии. Геометрические орнаменты. 1) Сколько осей симметрии имеет ...Общие понятия о симметрии. Элементы симметрии
План. Введение Термин симметрии Элементы симметрии. Введение. При обработке металла под давлением мы имеем дело с поликристаллами. Одним из важных ...Мир геометрических фигур
Цели и задачи:. - Показать связь геометрии с реальным миром Показать возможности применения геометрии. Подготовительный(чтение специальной литературы.) ...Красота и гармония в симметрии
Цели:. Научиться распознавать виды симметрии Найти симметричные фигуры вокруг нас Исследовать симметричные фигуры и показать их красоту. Я в листочке, ...История симметрии
Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей ...История изучения симметрии в природе
Оглавление: Введение………………………………………………………………………….2 Глава 1. Симметрия в точных науках………………………………………..3 1.1. Геометрия…………………………………………………………………….4 ...Группы симметрии фигур
Немного теории. Фигуру называют центрально-симметричной, а точку О – ее центром симметрии, если преобразованием симметрии относительно точки о фигура ...Виды симметрии в геометрии
1. повторить осевую и центральную симметрии; 2. познакомиться с зеркальной симметрией; 3. закрепить знания по видам симметрии. Цель урока:. Введение ...Центральная и осевая симметрии в природе
оглавление. 1. Что такое симметрия? 2. Виды симметрии. 3.Проявление симметрии в живой природе. 4. Проявление симметрии в неживой природе. 5.Вывод. ...Виды симметрии
Определение. В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, ...Мир правильных многогранников
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Осевая и центральная симметрии
Что такое симметрия? Осевая симметрия. Построение осевой симметрии. Ценральная симметрия. Построение центральной симметрии. Симметрия в окружающем ...Мир симетрии
Мир симметрии. Повторить осевую и центральную симметрии; Познакомиться с зеркальной симметрией; Расширить свои представления о симметрии; Увидеть ...Осевая и центральная симметрии
Содержание. Щелкните мышкой на нужном вам заголовке. Настраиваем анимацию. 1. Осевая симметрия. 2. Фигуры, содержащие ось симметрии. 3. Фигуры, имеющие ...Конспекты
Такой он этот мир симметрии
Мастер – класс. Такой он этот мир симметрии. Автор Лихоносова Наталья Сергеевна, учитель. I. квалификационной категории, МОУ ...В мире симметрии
В мире симметрии. Цели:. Обучающая. Сформировать понятие симметрии, как геометрическое свойство фигур. Развивающая. . Продолжить формирование ...Симметрия. Ось симметрии
Тема:. Симметрия. Ось симметрии. Тип урока:. урок открытия нового знания. Цель урока. : расширение понятийной базы за счет введения понятия ...Симметрия. Виды симметрии
. Урок для 8 класса на тему «Симметрия. Виды симметрии». Содержание. . ...Оси симметрии
МКОУ СОШ. . с. Ивановка. Открытый урок в 1 классе. «Ось симметрии». Тукало С.А. Тема урока:. Ось симметрии. Цель урока:. ...Осевая и центральная симметрии
МБОУ ООШ с. Старосеменкино муниципального района Белебеевский район РБ. Учитель математики Федорова Роза Климовна. Тема урока: «Осевая и центральная ...Осевая и центральная симметрии
Конспект урока геометрии в 8 классе по теме. . «Осевая и центральная симметрии». Цели. Проверить усвоение изученных свойств четырёхугольников. ...Мир иррациональных уравнений
Методическая разработка занятия. в 11 классе «Мир иррациональных уравнений». Раздел программы:. алгебра и начала математического анализа «Мир ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:16 сентября 2019
Категория:Математика
Классы:
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию