Конспект урока «Такой он этот мир симметрии» по математике

Мастер – класс

Такой он этот мир симметрии.

Автор Лихоносова Наталья Сергеевна, учитель I квалификационной категории, МОУ СОШ № 2

г. Миллерово

2012-2013

Такой он этот мир симметрии.

«Симметрия является той идеей, посредством которой, человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».

Цели:

1. образовательная

• Дать представление о понятии осевой симметрии;

• Показать учащимся связь математики с другими областями науки, искусством и реальной действительностью;

2. Развивающая

• Формировать умения наблюдать, подмечать закономерности, обобщать и делать выводы;

• Развивать любознательность, интеллектуальную сферу личности;

• Развивать умение учебно-познавательной деятельности

3. Воспитывающая:

• Воспитывать любовь к математике, к своей малой Родине.

Ход мастер класса

(Звучит музыка с повторяющимися аккордами

Смена слайдов с изображением березы и семьи).

Уж на Руси так исстари ведется,

Что счастье человеку там, где дом.

Не стены и не мебель его красят,

А близкие – любовью и теплом.

Мы русские, и нам до боли свято,

Все то, что связано со светом и добром:

Россия, дочка с сыном, папа, мама

И нежная березка под окном.

В ее листе – живительная сила,

Она хранит семью и весь наш дом,

Она гармонию в наш дом приносит

И наполняет жизнь любовью и теплом.

В моих руках символическая веточка березы.

Народная примета гласит: «Если сорвать листик с березы, растущей у дома, сложить его пополам, и обе половинки этого листа совпадут, то это показывает, что дом наполнен любовью, гармонией и добром».

Я предлагаю каждому из вас сорвать по листику, проверить данную примету и убедиться в том, что гармония есть и в вашем доме.

Но красота и гармония мира строятся на сухих математических терминах. С одним из таких терминов нам сегодня и предстоит познакомиться. Как вы думаете о чем сейчас пойдет речь?

Много веков люди восхищаются красотой, созданной самой природой. Крылья бабочки, снежинки, лисья клена и многое другое являлось своеобразной подсказкой для открытия такого явления как симметрия. Известный математик Герман Вейль писал: «симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту, совершенство»

Сегодня мы прикоснемся к удивительному математическому понятию – симметрия, познакомимся с симметрией не только в математике, но и…

А где же еще мы встречаемся с симметрией?

С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Греческое слово «симметрия» означает «соразмерность», «пропорциональность», «одинаковость в расположении частей». Однако, часто под словом «симметрия» понимают более широкое понятие: регулярность смены каких-либо явлений (Слайды времен года, дня и ночи и т. д.), уравновешенность левого и правого, равноправие природных явлений. Фактически мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. В психологии и морали широко использовалось понятие симметрии. А симметрия, понимаемая как покой, уравновешенность, противостоит хаосу и беспорядку.

Математически строгое определение симметрии сформировалось сравнительно недавно – в 19 веке. В наиболее простой трактовке известного немецкого математика Германа Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали. Современное представление о симметрии предполагает неизменность объекта по отношению к каким-то преобразованиям, выполняемым над ним. В математике рассматривается несколько видов симметрии.

1 задание (3 мин)

• Возьмем лист бумаги, сложим его пополам и вырежем какую-нибудь фигурку. Теперь развернем фигуру и посмотрим на линию сгиба.

Вопрос: Какую функцию выполняет эта линия?

Предполагаемый ответ: Эта линия делит фигуру пополам.

Вопрос: Как расположены все точки фигуры на двух получившихся половинках?

Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.

• Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.

Основным видом симметрии является осевая, с этим видом мы чаще всего встречаемся.

Именно этот вид симметрии, по мнению математиков, определяет свойства и важнейшие законы нашего мира.

• Кто может сформулировать определение симметрии?

Определение. Фигура называется симметричной относительно прямой, если эта прямая делит фигуру на две равные части, совпадающие при перегибании по этой прямой. (слайд 9).

Задание 2 (2 мин).

(на фоне музыки «Снег кружится»)

А сейчас я предлагаю посмотреть в окно. …Зима, снег, снежинки… Давайте вырежем снежинку.

• Вырезать снежинку, найти ось симметрии, охарактеризовать ее.

Задание 3 (5 мин).

• Перед вами лежит круг.

Вопрос: Определить, как проходит ось симметрии?

Предполагаемый ответ: По-разному.

Вопрос: Так сколько осей симметрии имеет круг?

Предполагаемый ответ: Много.

– Правильно, круг имеет множество осей симметрии.

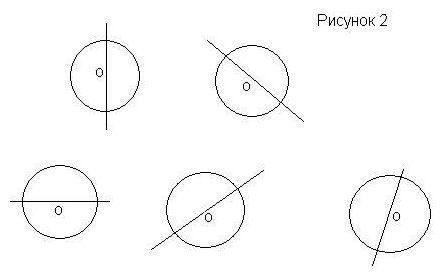
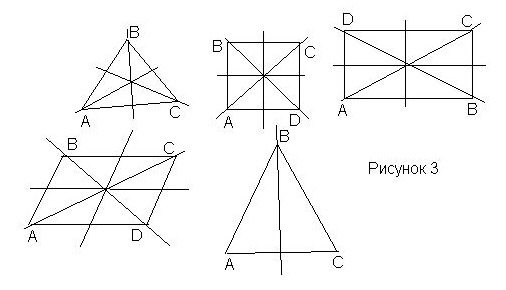
Вопрос: Какие, из предложенных вам фигур, имеют не одну ось симметрии?

Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.

А если говорят о симметриями в пространстве то имеют в виду Зеркальную симметрию

Предлагаю провести опыт

На одном листе у меня написано слово «КОФЕ», а на другом – «ЧАЙ». Положим эти листики по очереди перед зеркалом на стол. Посмотрите, что получилось? Зеркало не перевернуло слово «КОФЕ» и до неузнаваемости изменило слово «ЧАЙ». Как вы считаете, почему это произошло? (Так как буквы К, О, Ф, Е имеют горизонтальную ось симметрии, которая проходит через середину каждой буквы, а Ч,А,Й не симметричны относительно этой оси).

Рассмотрим гармонию в алгебре на примере следующих уравнений: рассмотрим уравнение линии.

х³+у³ – 3ху=0

А эта линия называется Декартов лист (слайд). В честь французского философа, математика, физика, физиолога Рене Декарта. (31.03.1596 – 11.02.1650).

Обратите внимание на уравнение, которым задается эта кривая. Как вы думаете, почему его рассматриваем в разделе симметрия?

Если в нем заменить х на у, а у на х, то получится то же самое уравнение. Такое уравнение называется симметричным.

рассмотрим еще несколько уравнений:

4х⁴ -2х³ - 10х² + 2х + 4 = 0
или 6х⁴ - 35х³ + 62х² - 35х +6 = 0

Уравнения такого вида называются возвратными или симметрическими. Почему?

Вывод: Мы рассмотрели примеры использования симметрии в алгебре, на примерах функций.

Симметрия сквозь века. (слайды 16 – 18).

С симметрией мы встречаемся не только на уроках геометрии и алгебры.

В своих размышлениях над картиной мира человек с давних пор активно использовал идею симметрии в рисунках, орнаментах, предметах быта. Вы, наверное, обращали внимание на то, как строго симметричны формы античных зданий, гармоничны древнегреческие вазы, соразмерны их орнаменты.

Красота и гармония тесно связаны с симметрией, это подметили еще древние архитекторы и художники. Слово симметрия происходит от греческого слова, которое означает «такая же мера».

Проходя сквозь века, термин «симметрия» обрастал различными толкованиями. Симметрия – это некая «средняя мера, гармония», - считал Аристотель.

Великий живописец и инженер XV в. Леонардо да Винчи тоже употреблял слова «гармония», «равновесие» в значении «симметрия», считая, что при создании художественного произведения главную роль играют пропорциональность и гармония, под которыми он понимал симметрию.

Его личность и записи овеяны тайнами. Одной из самых известных является портрет Моны Лизы (Джоконды)

Существует много версий об истории создания этого портрета, о загадочной улыбке Джоконды. Вот одна из них: Однажды Леонардо да Винчи получил заказ от банкира Франческо дель Джокондо написать портрет его жены, Моны Лизы. Женщина не была красивой, но привлекала своей простотой и естественностью. Она была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, женщина улыбнулась.

Предлагаю и нам познакомиться с этой сказкой.

Мне понадобится ваша помощь. Прочитать эту сказку по ролям.

Сказка – инсценировка.

( ролевая игра с участниками )

Жил был бедный человек, и было у него четыре сына. Пришла за отцом смерть. Позвал он сыновей и сказал…

Старик.

Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастье. Пусть каждый из вас чему-нибудь научится, чтобы прокормиться.

Ведущий

Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи.

Прошло три года.

1 – й Брат.

Итак, я первый вернулся домой. Я плотник и неплохой. Срублю-ка я дерево, обтешу его и сделаю из него женщину (работает, затем отходит в сторону).

2 – й Брат.

О, да здесь деревянная женщина. Красивая! Сошью-ка я ей красивую шелковую одежду. Ведь я искусный мастер – портной (работает, затем отходит в сторону).

3 – й Брат.

Вот это да! Деревянная скульптура женщины в прекрасной одежде! Украшу-ка я ее драгоценными камнями и золотом – ведь я ювелир (украшает, отходит).

4 – й Брат.

Какие мои братья мастера! А я не умею ни плотничать, ни шить, ни заниматься ювелирным делом. Я умею только слушать, что говорят земля, деревья, травы, звери и птицы, а еще я умею петь песни

Ведущий.

Песней он оживил девушку. А братья бросились к ней с просьбой выбрать одного из них в мужья.

Девушка.

Ты меня создал – будь мне отцом. Вы меня одели и украсили – будьте мне братьями. А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь. (Персонажи инсценировки уходят.)

Ведущий.

Закончив сказку, Леонардо да Винчи взглянул на Мону Лизу и увидел, что глаза ее засияли и лицо озарилось светом; она вздохнула, провела по лицу рукой, сложила руки и приняла обычную позу.

Но дело было сделано – художник пробудил равнодушную статую, улыбка блаженства, медленно исчезая, осталась в уголках рта и трепетала, придавая лицу изумительное. Загадочное и чуть лукавое выражение, как у человека, который узнал тайну, и, бережно ее храня. Не может сдержать торжество. Такова одна из версий существования загадочной улыбки Джоконды. Посмотрите как она прекрасна!

Роль симметрии в познании природы (слайды)

Если внимательно приглядеться к стеблю растения, то окажется, что и здесь действует закон симметрии. Пример тому листья, цветы и плоды растений. Веточка акации обладает осевой симметрией. Если прочертить вертикальную прямую вдоль центральной прожилки листа и поставить зеркальце, вдоль прочерченной прямой, то отраженная в зеркальце половинка фигуры дополнит ее до целой.

Осевая симметрия встречается и в животном мире. Несколько примеров: крылья бабочки, морские простейшие, двусторонняя симметрия человеческого тела. Среди врачей существует мнение, что причинами наших болезней являются не только и не столько вирусы и прочие вредные факторы среды, сколько нарушения конструкции тела. «Симметричные» животные живут дольше, чем «несимметричные». Асимметрия лица – это показатель старения.

Симметрия господствует не только в природе, но и в творчестве человека: архитектуре, живописи, музыке, литературе.

Прекрасные образы симметрии демонстрируются в произведениях архитектуры. Примеры – египетские пирамиды, древнегреческие постройки: церковь Вознесения в Коломенском, храм Василия Блаженного в Москве.

Огромное влияние симметрии в живописи. На рисунках это хорошо видно.

Для усиления эстетического воздействия симметрия используется и в поэзии, и в музыке. На Руси с давних пор сложилась своя система звонов колоколов, колокола звонили по-разному, в каждом случае со своим ритмом, со своей симметрией. Музыка, исполняемая на музыкальных инструментах или воспроизводимая человеческим голосом, также полна симметрии.

Симметрия есть и в стихотворениях

В этот год осенняя погода

Стояла долго на дворе

Зимы ждала, ждала природа

Снег выпал только в январе.

Чередование рифм, ударных слогов, ритмичность и интонация придают прелесть пушкинскому стихотворению.

Значит получается, что когда мы, говорим о гармонии, красоте, мы касаемся симметрии.

Дальше поговорим о симметрии в неживой природе.

(слайды 32 – 33).

На первый взгляд мир неживой природы кажется лишенным симметрии и порядка, но это не так. Ярким доказательством являются кристаллы. Симметрия кристаллов является следствием их внутреннего строения. Загадочная снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией.

Сегодня вы убедились, что в окружающей нас действительности очень много симметричных объектов. Это делает мир вокруг нас красивым и гармоничным.

А сейчас… Давайте симметрию почувствуем.

У вас на столе есть заготовка, из которой я предлагаю каждому из вас с помощью осевой симметрии сделает свою птицу счастья.

Птица счастья

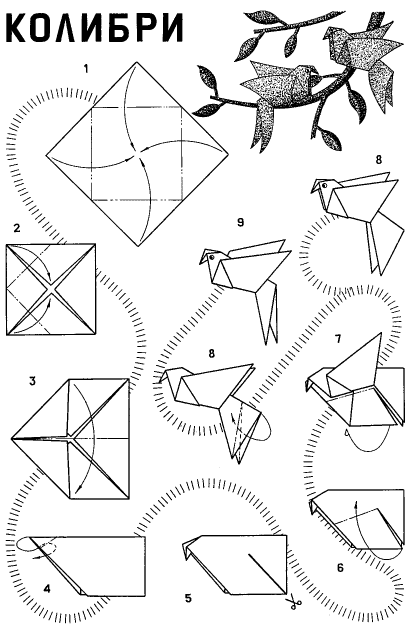
У каждого из нас - сделанная собственными руками птица счастья. Я искренне надеюсь, что она принесет радость, укрепит здоровье и сохранит гармонию в ваших сердцах.

А свою птицу счастья я оставлю на этой веточке, как напоминание о нашей встрече, позволившей ближе узнать и понять друг друга.

Гармония чисел, гармония линий,
Мира гармонию мы изучили.
Строгая логика – щит от разлада,
Кружево формул – сердцу награда.
Но путь к ней неровен – от впадин до всплесков,
Мрачен иль светится солнечным блеском.
К тайнам извечным разум влекущий,
Тот путь бесконечный, осилит идущий.

Я желаю вам огромных успехов и гармония в отношениях с родными и близкими. Будьте здоровы и счастливы.

VI. Рефлексия.