Презентация "Пирамида. Сечения пирамиды" по математике – проект, доклад

Скачать презентацию (99.29 Кб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Презентацию на тему "Пирамида. Сечения пирамиды" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).

Скачать презентацию (99.29 Кб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Тема урока:

Пирамида. Сечения пирамиды.

Слайд 2

Слайд 3

Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD. Построить линейный угол двугранного угла, образованного плоскостью прямоугольника ABCD и плоскостью α.

Слайд 4

Способы задания плоскости

A B C a b

Слайд 5

Признак перпендикулярности прямой и плоскости

Слайд 6

Теорема о трех перпендикулярах

Слайд 7

Двугранный угол. Линейный угол двугранного угла.

Слайд 8

Признак параллельности прямой и плоскости

Слайд 9

Через вершину прямого угла С прямоугольного треугольника ABC проведена плоскость α параллельная гипотенузе на расстоянии 1 м от нее. Катеты AC и BC равны соответственно 6 м и 8 м. Найти двугранный угол между плоскостью треугольника ABC и плоскостью α.

С A1 D B1

Слайд 10

Слайд 11

XY – ребро двугранного угла (; ABCD). XY || BD – по условию. Если AFBD, то AF  XY. Т.к. α|| BD, то MN || BD, EF || OO1, тогда EF  MN, то по т. т. п. AE  MN. Значит плоскость (AEF)  BD, а, следовательно, и XY. Т.о. FAE – линейный угол двугранного угла с ребром XY.

Слайд 12

Слайд 13

Задача №2. Основанием пирамиды SABC служит равнобедренный треугольник ABC, у которого С = 120°, AC = BC = 12. Высота пирамиды совпадает с боковым ребром SA и двугранный угол с ребром BC равен 30°. Вычислить площадь полной поверхности пирамиды.

Дано: SABC – пирамида. SAABC ACB = 120° AC = BC = 12  SDA = 30° Найти: Sполн.

Слайд 14

Список похожих презентаций

Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.

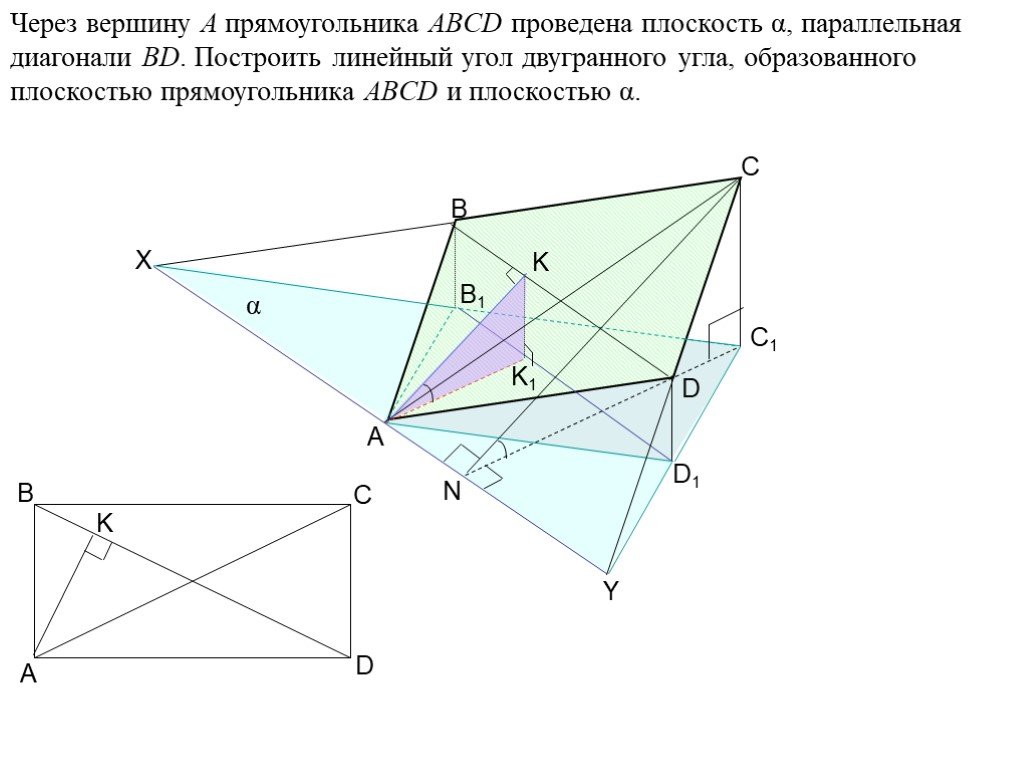
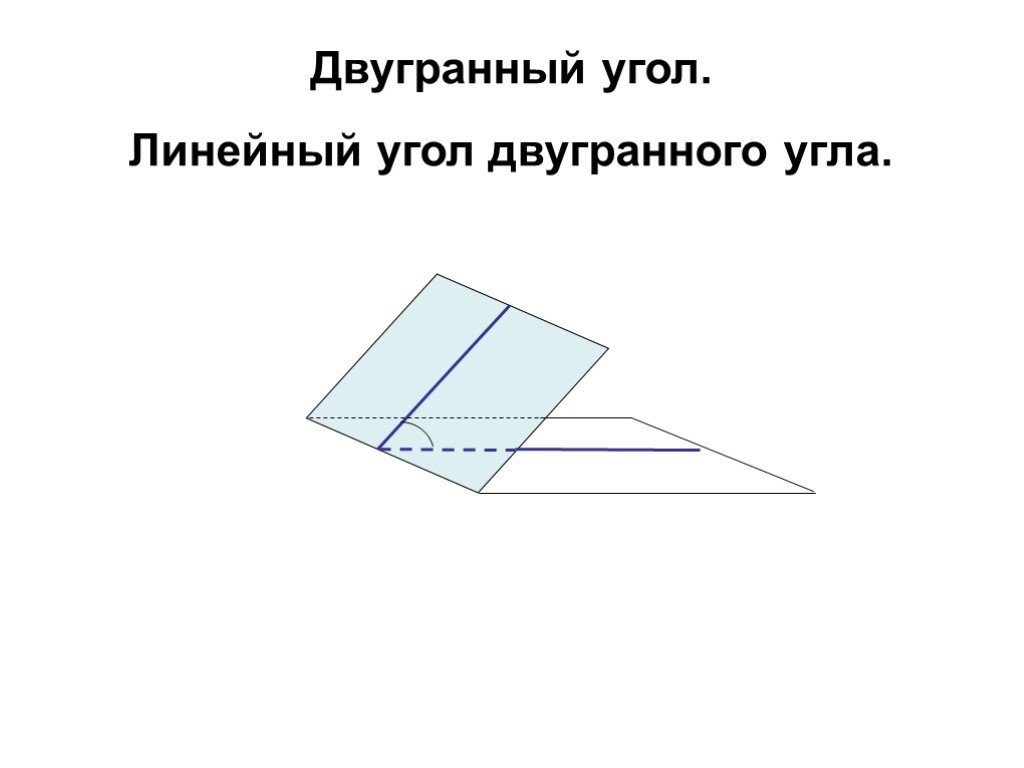
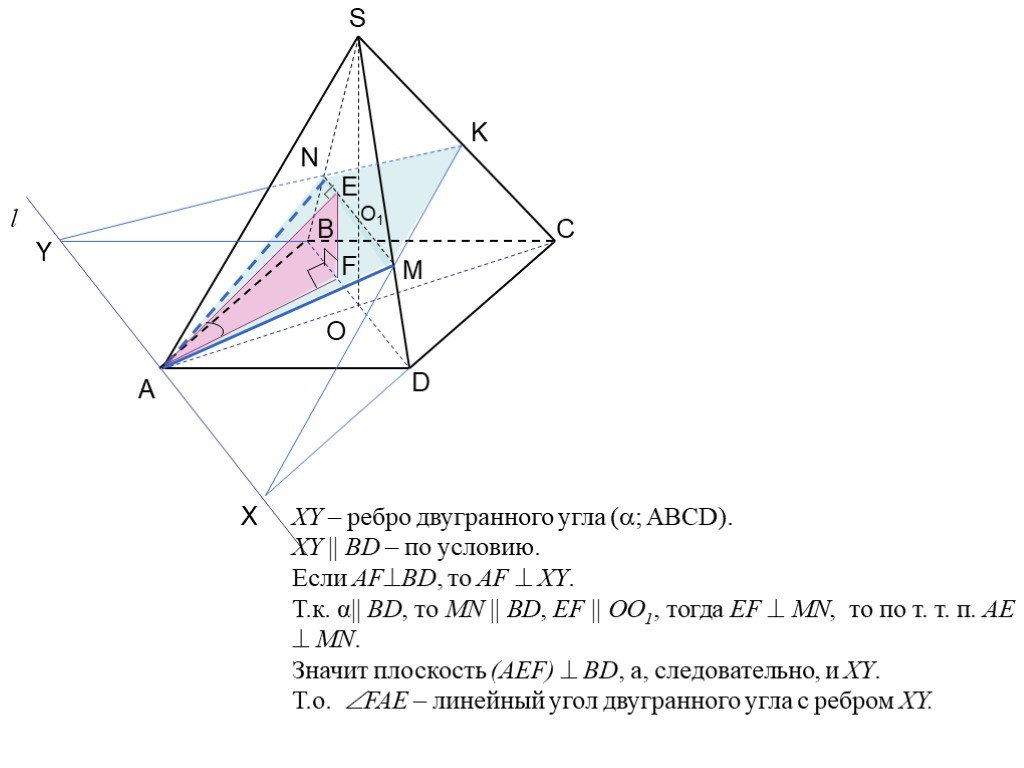
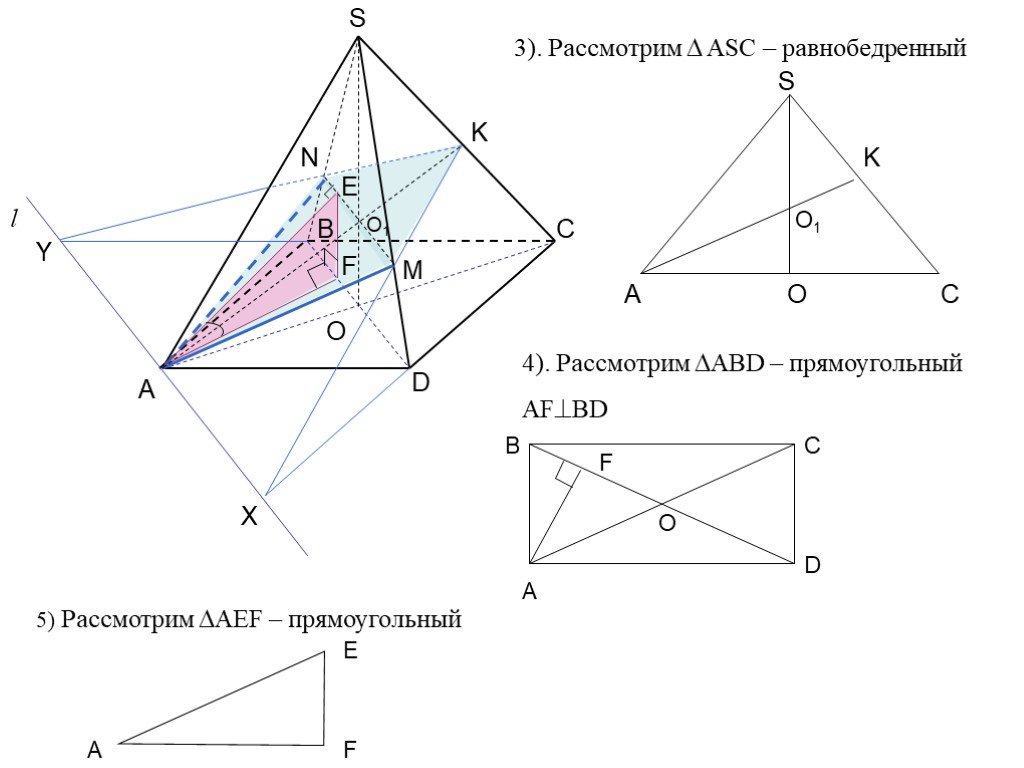
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...

Сечения пирамиды

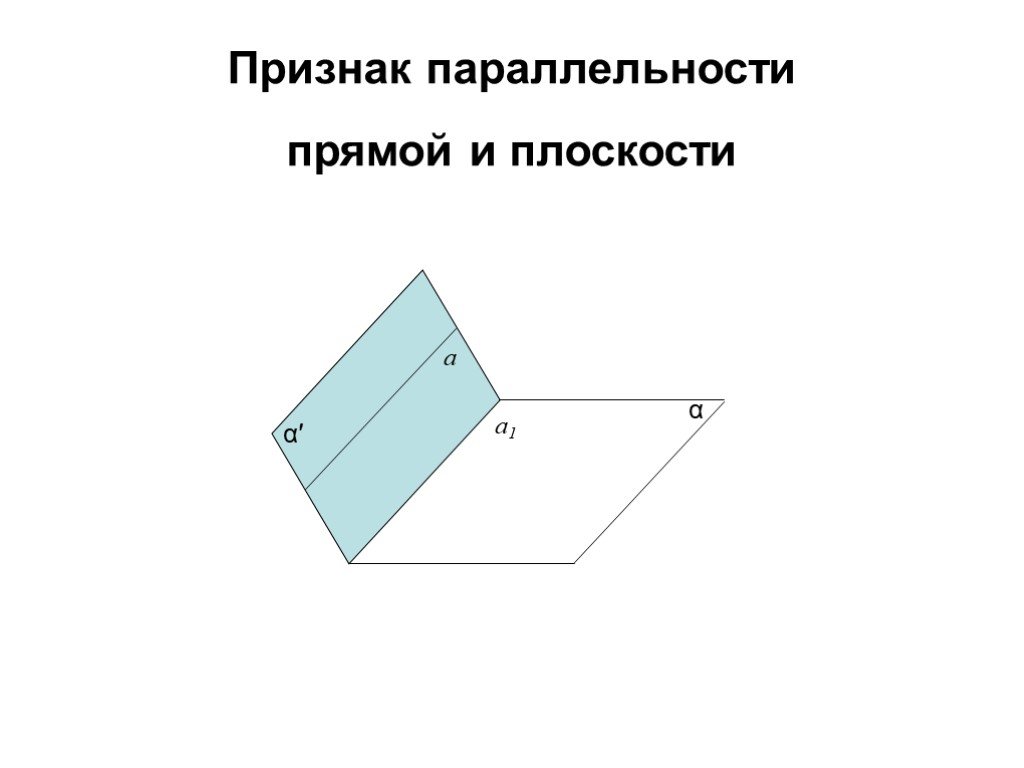
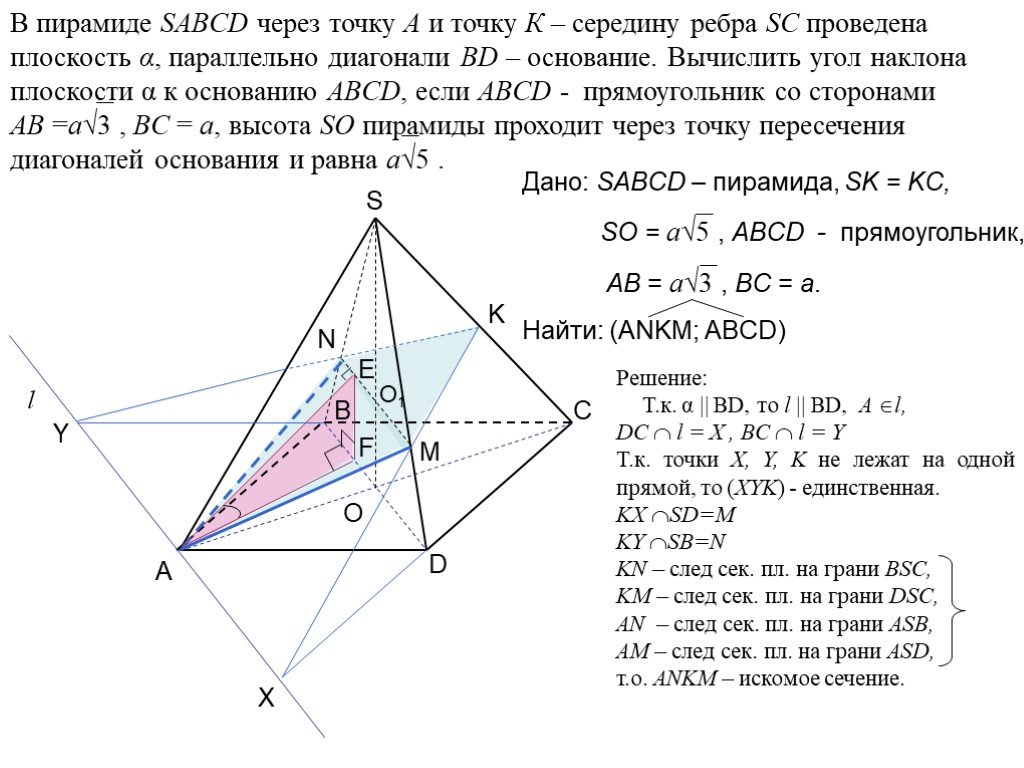
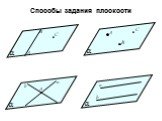
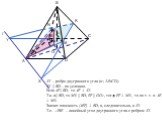
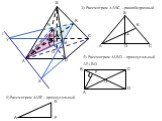
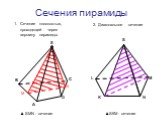
3. Сечение пирамиды плоскостью с заданным следом. A B C F P Q MNPQ - сечение. 4. Сечение пирамиды плоскостью, параллельной основанию. MNKP - сечение ...

Сечения пространственных фигур

...

Сечения многогранников плоскостью

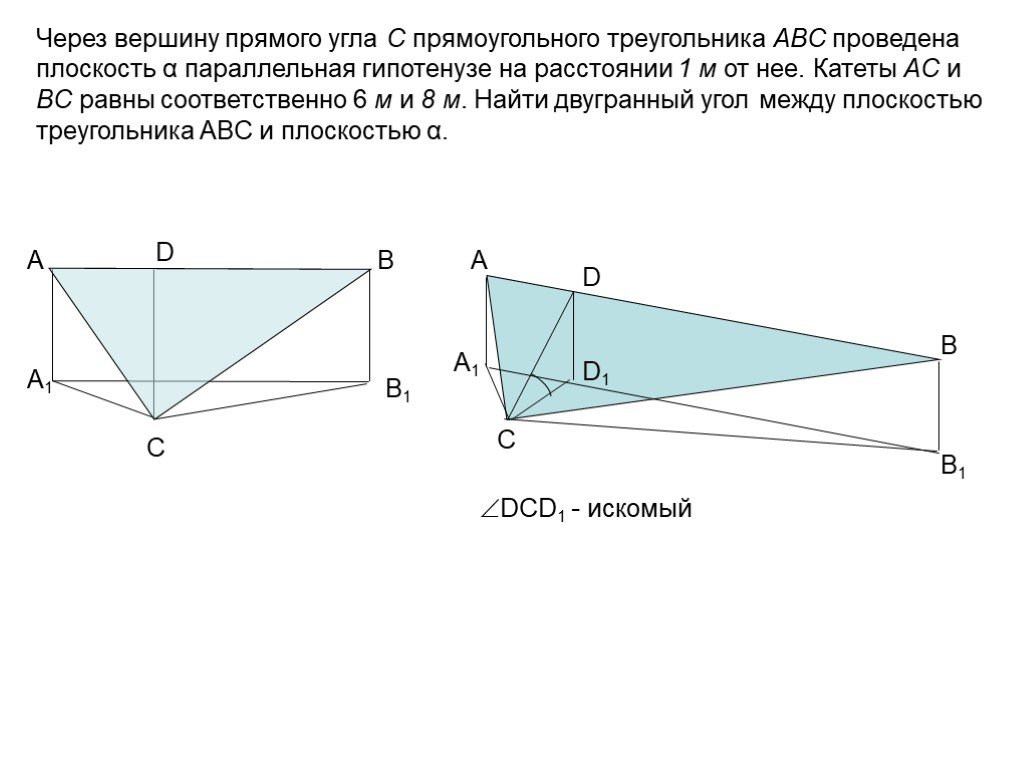
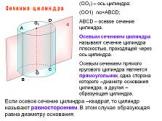
Работа с текстом задачи. Задача. Построить сечение пятиугольной призмы плоскостью, проходящей через три точки, одна из которых лежит в плоскости верхнего ...

Сечения конуса и цилиндра

Математический диктант. 1 1 вариант 2 вариант. Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса? Какая фигура получается ...

Сечения

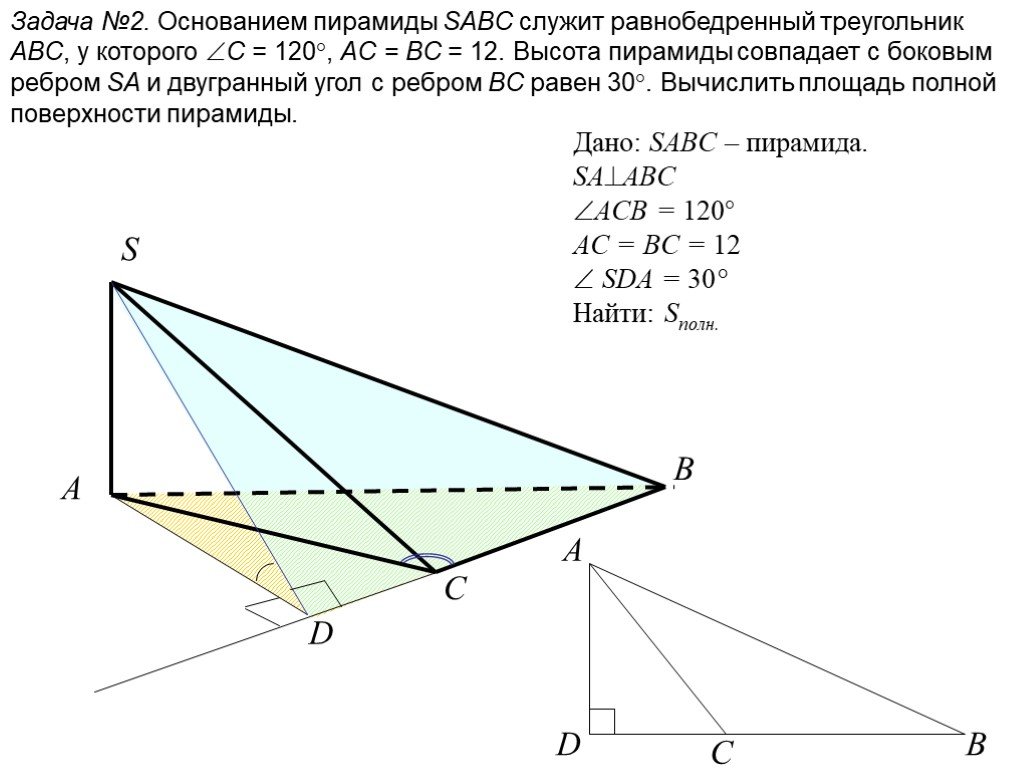
Сечения. Геометрия 10 -11. формирование и развитие пространственных представлений; выработка навыков решения задач на построение сечений простейших ...

Свойства пирамиды с равными боковыми ребрами

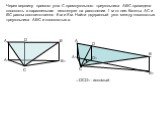
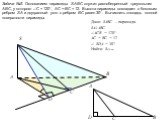
Теорема 1.1. Дано: МАВС - треугольная пирамида, МО – высота пирамиды, боковые ребра равны АМ=ВМ=СМ. Доказать: АО = ВО = СО. Теорема 1.2. Дано: МАВС ...

Египетские пирамиды

Почему Египетские пирамиды называют немым трактатом по геометрии? Автор: Зеленцов Роман 10а класс. МОУ СОШ с.Становое. 2008 год. Цель: научиться определять ...

Пирамида

Пирамида— многогранник, основание которого многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают ...

Пирамида

Содержание. Определение пирамиды Правильная пирамида Усеченная пирамида Решение задач Итог урока Список литературы. А1 А2 Аn Р. Многогранник, составленный ...

Определение призмы, пирамиды

Пусть даны две параллельные плоскости  и β. Построим в плоскости  произвольный n-угольник A1A2…An. A1 A3 An An-1  β B1 B3 Bn Bn-1. Через его вершины ...

Объем пирамиды

Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...

Объём пирамиды

ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ. Цель работы:. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО ...

Объем пирамиды

Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...

Загадка пирамиды

I Вступление II. Из истории. 1. Пирамида Джосера 2. Пирамида Хеопса III. Об Александре Голоде IV. Пирамида и архитектура 1. Исследования и практическое ...

Сечения тетраэдра

Информация для учителя. Цель создания этой презентации состоит в том, чтобы наглядно продемонстрировать алгоритмы построения точки пересечения прямой ...

Сечения цилиндра

...

Пирамида

План. Определение Элементы пирамиды Свойства пирамиды Правильная пирамида Свойства правильной пирамиды Прямоугольная пирамида Поверхность пирамиды ...

Решение задач по теме "Пирамида"

Цели урока. Изучить мнемонический прием. Вывести формулы перехода основных углов в правильных пирамидах. Научиться применять мнемонический прием ...

Пирамида

Правильная усеченная пирамида. Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды Высота боковой грани правильной ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.