Презентация "Свойство биссектрисы" по математике – проект, доклад

Замечательные точки треугольника. Урок 1. Свойство биссектрисы угла

Презентация выполнена учителем математики МБОУ СОШ № 22 Лисицыной Татьяной Петровной, п. Пересыпь, Темрюкский район, Краснодарский край

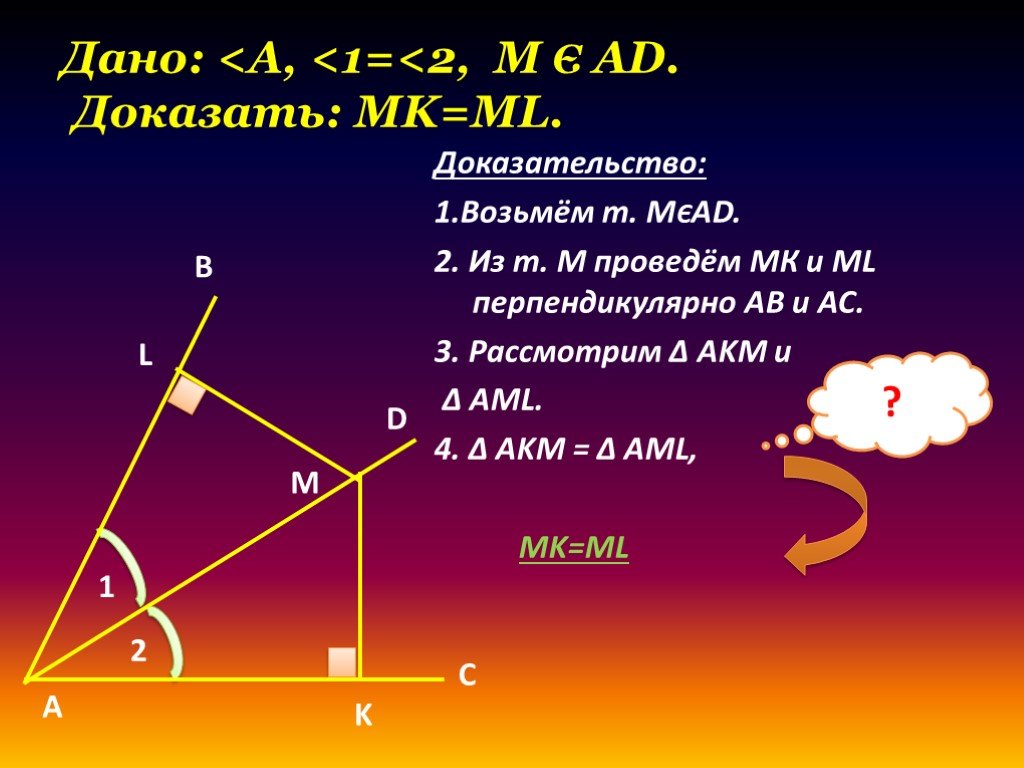
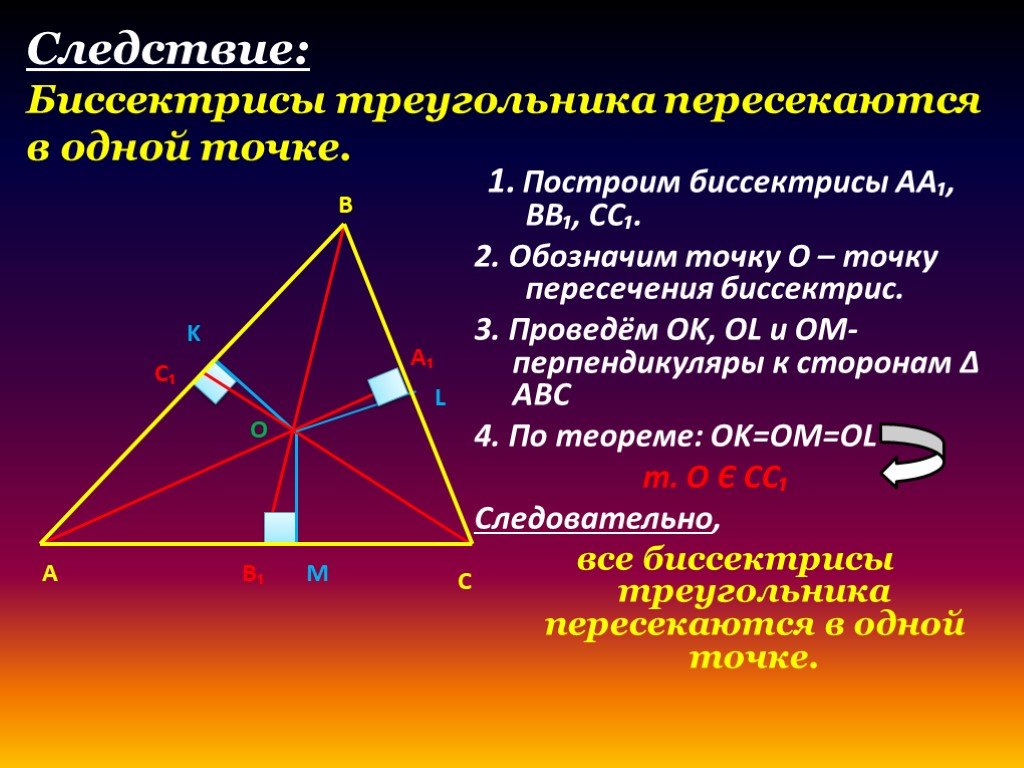
Цели урока:

Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Учить применять данные теоремы и следствие при решении задач.

Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии. Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения - никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

C каждым треугольником связаны четыре точки: • точка пересечения медиан; • точка пересечения биссектрис; • точка пересечения серединных перпендикуляров; • точка пересечения высот. Эти четыре точки называют замечательными точками треугольника. Почему они «Замечательные»? Это нам и предстоит узнать.

Свойство биссектрисы

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

Дано:

Доказательство: 1.Возьмём т. МЄAD. 2. Из т. М проведём МК и ML перпендикулярно AB и AC. 3. Рассмотрим Δ AKM и Δ AML. 4. Δ AKM = Δ AML, MK=ML

? А 2 1

Следствие: Биссектрисы треугольника пересекаются в одной точке.

1. Построим биссектрисы АА₁, BB₁, CC₁. 2. Обозначим точку O – точку пересечения биссектрис. 3. Проведём OK, OL и OM-перпендикуляры к сторонам Δ ABC 4. По теореме: OK=OM=OL т. О Є СС₁ Следовательно, все биссектрисы треугольника пересекаются в одной точке.

O

№ 676 б. Cтороны угла А, равного 90°, касаются окружности с центром О и радиусом r, ОА = 14 дм. Найдите: r.

Решение: Проведём радиусы OP и OH из центра окружности в точки касания. OP AP, OH AH 3. AO – биссектриса угла 4. Δ AOP – прямоугольный. По теореме Пифагора: AO²=OP²+AP² AO²=r²+r², 2r²=14², r=7√2. Ответ: r=7√2дм.

№678 а – дополнительно.

Оформить и решить самостоятельно. Ответ: 46˚

Использованные ресурсы: 1. Учебник «Геометрия 7-9»; авт: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. М., Просвещение, 2007г. 2. Рисунки треугольников: http://www.google.ru/search?q=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8+%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0&hl=ru&newwindow=1&prmd=imvns&tbm=isch&tbo=u&source=univ&sa=X&ei=_j5CT9zvLK_Q4QSShuyACA&ved=0CCIQsAQ&biw=1247&bih=864.