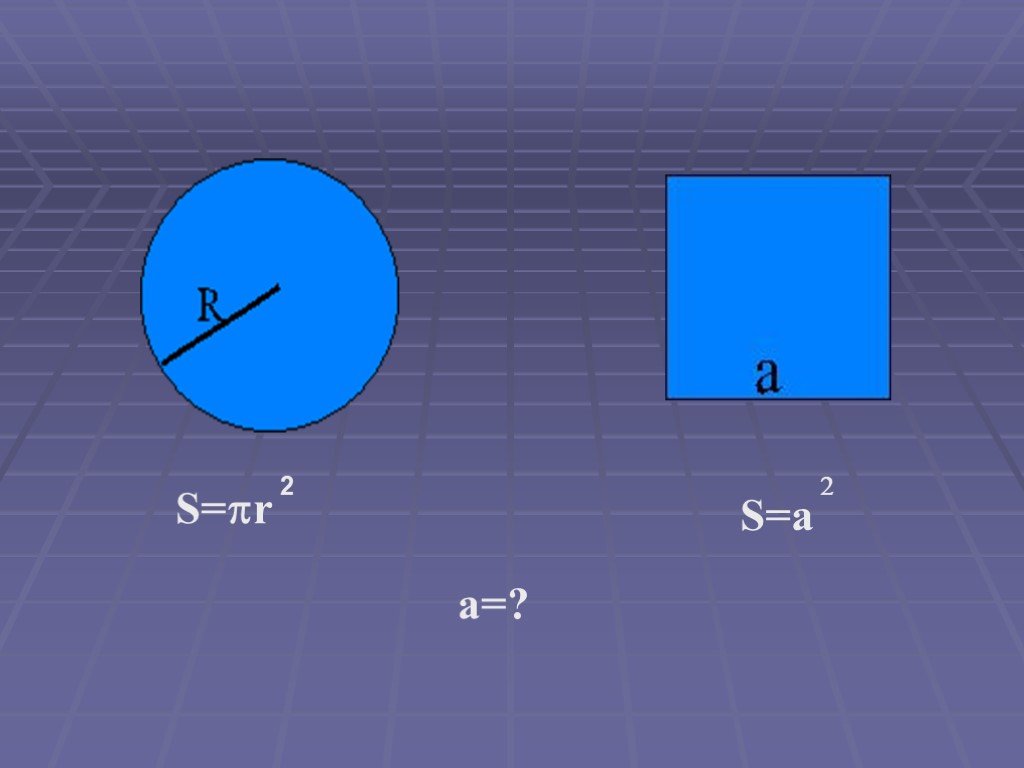
Презентация "Великие задачи математики. Квадратура круга" по математике – проект, доклад
Презентацию на тему "Великие задачи математики. Квадратура круга" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
Великие ученые-математики
Содержание Евклид Пифагор Виет Декарт Ферма Эйлер Гаусс Чебышев Ковалевская Завершить показ. Евклид (3 век до н. э.) - древнегреческий математик. ...Задачи на площадь круга
Площадь сектора. Круговым сектором, или просто сектором, называется общая часть круга и центрального угла с вершиной в центре этого круга. Для нахождения ...Великие математики прошлого
Великие математики прошлого. (гг. рождения и смерти неизвестны, вероятно, 1 в.). Знаменитая "Формула Герона" для площади треугольника S = , где р ...Великие русские математики
Лобачевский Николай Иванович (1 декабря 1792 года – 12 февраля 1856 года). Профессор математики Ректор Казанского университета Создатель новой теории ...Великие математики и их открытия
Ковалевская Софья Валерьевна (1850-1891). . Русский математик, писательница, первая русская женщина-профессор. В 1874 была удостоена ученой степени ...Великие математики прошлого
Пифагор. (родился ок. 580 г. и умер ок. 500 г. до н.э.). . По совету Фалеса 22 года Пифагор набирался мудрости в Египте. В Вавилон он попал не по ...Великие математики древности
Архимед родился около 287 г. до н.э. Историки древности Полибий, Ливии, Плутарх мало рассказывали о его математических заслугах, от них до наших времен ...Великие математики
Архимед. Архимед как математик. До нас дошло 13 трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» (в двух книгах) Архимед устанавливает, ...Великие математики древности
ВЕЛИКИЕ МАТЕМАТИКИ ДРЕВНОСТИ. Аристотель Аполлоний Пергский Демокрит Евклид Пифагор Рене Декарт Фалес Милетский. Демокрит (ок. 460–370 гг. до н.э.). ...Великие математики
АРХИМЕД (ок. 287-212 гг. до н.э.). Об Архимеде - великом математике и механике - известно больше, чем о других ученых древности. Прежде всего достоверен ...Великие математики
В современном мире Пифагор считается великим математиком и космологом древности. Античные авторы нашей эры отдают Пифагору авторство известной теоремы: ...Великие математики
570 г. до н.э. Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 ...Великие математики
. Задания для выбора участников I тура. Как одним словом назвать сумму длин всех сторон? периметр Сколько горошин может войти в пустой стакан? одна ...Великие математики
ЭТИ УЧЕНЫЕ СЫГРАЛИ ОГРОМНУЮ РОЛЬ В РАЗВИТИИ МАТЕМАТИКИ. ЕВКЛИД. древнегреческий математик. Работал в Александрии в 3 в. до н. э. Главный труд «Начала» ...Великие математики
В современном мире Пифагор считается великим математиком и космологистом древности, однако ранние свидетельства до III в. до н. э. не упоминают о ...Великие математики
Блез Паскаль (1623-1662). Блез Паскаль был сыном Этьена Паскаля, корреспон- дента Мерсенна. Блез быстро развивался под присмотром своего отца, и уже ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Геометрические построения в школьном курсе математики
План. 1. Основные понятия теории геометрических построений: сущность геометрических построений; основные инструменты построений и их аксиомы; простейшие ...Астрономические координаты. Секция: математики
Целью моей работы является нахождение и анализ необходимой информации по данной теме. Задачей является детальное рассмотрение сфер применения на практике ...Конспекты
Великие математики
МБОУ Уджейская ООШ. общешкольный классный час. по теме:. «ВЕЛИКИЕ МАТЕМАТИКИ». Подготовила материал и. . провела –. В.А. Овчинникова. ...Великие математики России. С.В. Ковалевская
План-конспект внеклассного мероприятия. «Великие математики России. С.В. Ковалевская». . ФИО. . Ракитина Эльвира Альбертовна. . ...Повторение курса математики начальной школы
Никифорова Марина Николаевна. учитель математики ГБОУ СОШ № 1968 г.Москвы. . Конспект урока математики. . по теме «Повторение курса математики ...Площадь круга
Урок по математике. в 6 классе «Площадь круга». Разработал:. Макарова Татьяна Павловна, учитель математики ГБОУ СОШ № 618 г. Москвы. Учебник:. ...О вреде наркотиков – языком математики
Муниципальное казенное образовательное учреждение. «Днепровская средняя общеобразовательная школа». Новодугинский район Смоленская область. ...Сложение 57+40, 40+57. Применение переместительного закона математики
Урок математики. 3 класс. «Сложение 57+40, 40+57. . . Применение переместительного закона математики». 5 февраля ...Решение задач. Обратные задачи
. . Урок математики 2 класса. Тема урока: Решение задач. Обратные задачи. Цель: . закрепить навык решения изученных задач. Задачи:. ...Развитие логического мышления на уроках математики
Развитие логического мышления. на уроках математики. в начальной школе. Учитель первой квалификационной ...Путешествие в мир математики
Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Урок-викторина. «Путешествие в мир математики». для учащихся ...Взаимно обратные задачи
Математика. Тема:. Взаимно обратные задачи. Цель:. Сформировать представление о взаимно обратных задачах, умение их распознавать и составлять задачи ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию