Презентация "Решение задач на построение графиков алгебраических функций" – проект, доклад
Презентацию на тему "Решение задач на построение графиков алгебраических функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
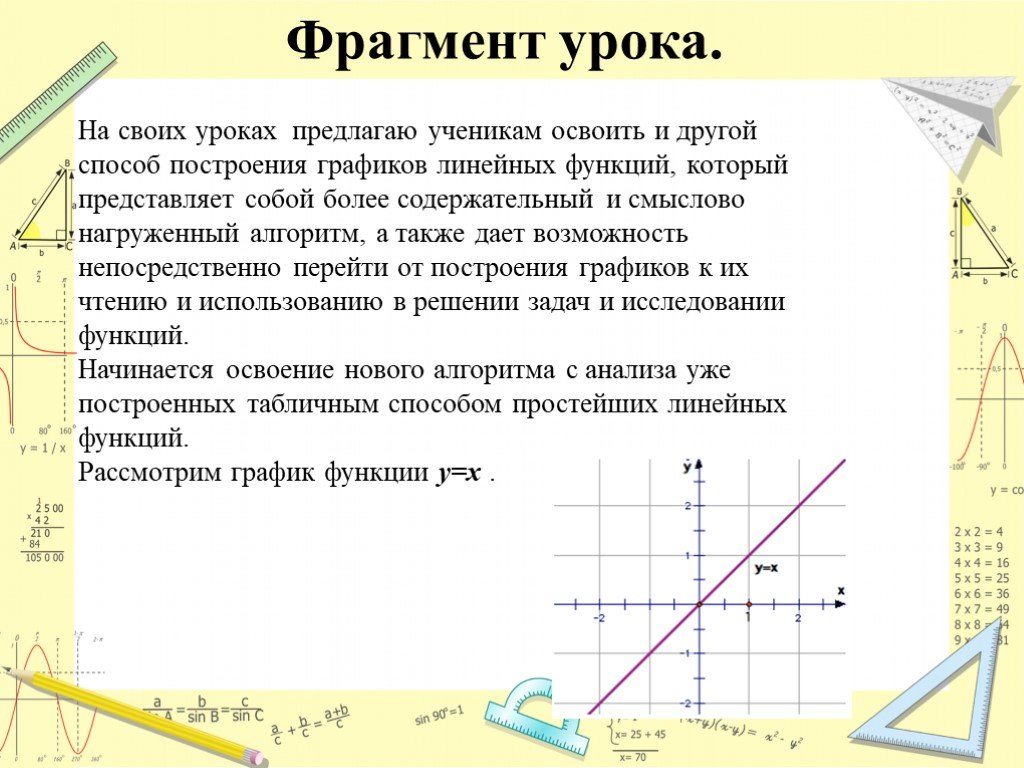
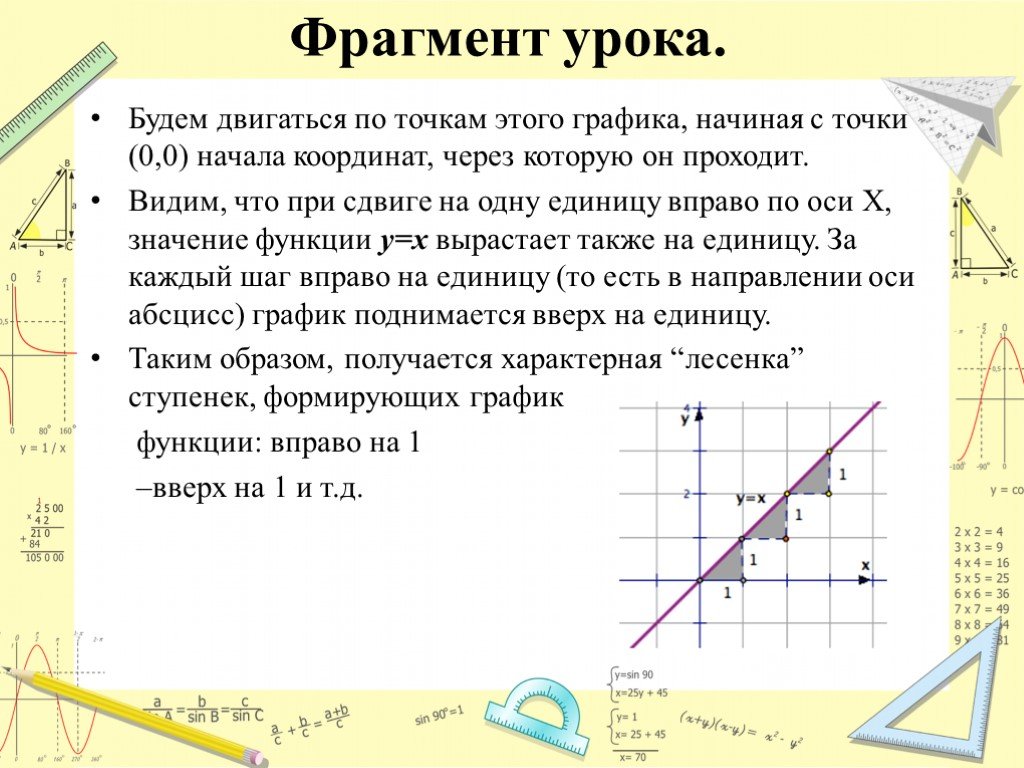
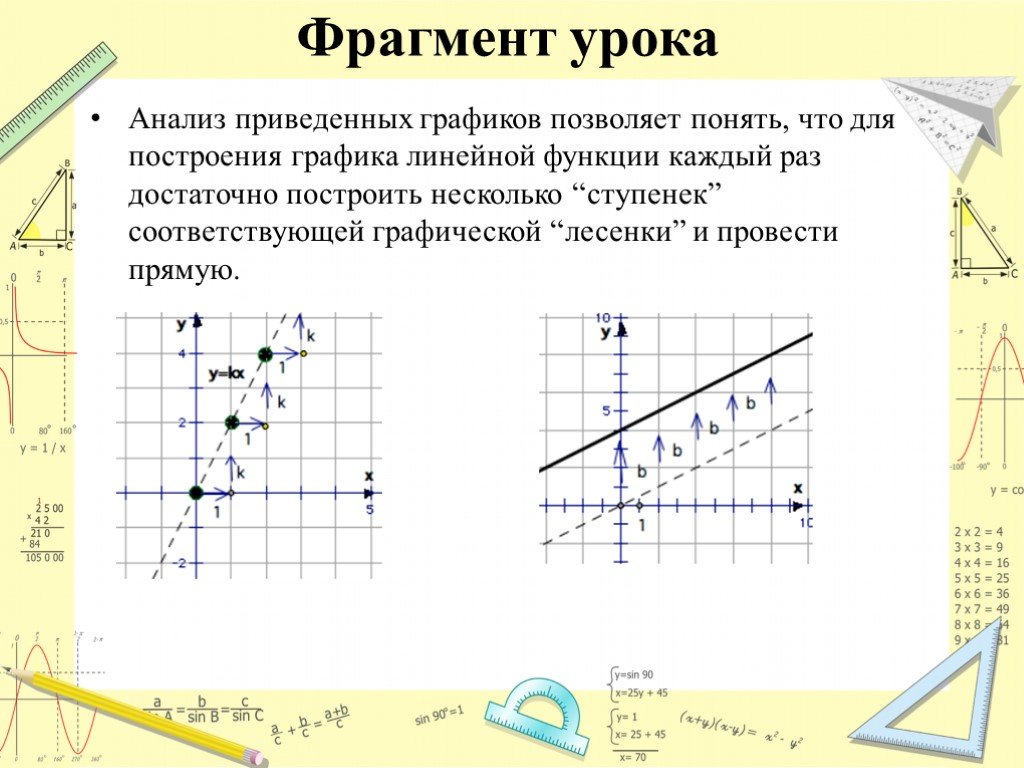
Слайды презентации
Список похожих презентаций
Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Арифметика Л.Ф. Магницкого. Задачи на сплавы и смеси
Цели моей работы. Познакомиться с биографией Леонтия Филипповича Магницкого Научиться решать задачи на сплавы, находить процентное содержание веществ ..."Взаимное расположение графиков функций"
угловой коэффициент прямой, условие параллельности прямых. ТЕМА УРОКА:. Давайте узнаем имя одного математика, который ввел обозначение функций. Для ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Примеры преобразования графиков функций»
у = х3 у = -х3 у = (х - 1)3 у = х3 + 1 у = 2х3 у = (2х)3 х = у3. у = х4 у = -х4 у = (-х)4 у = (х-1)4 у = х4-1 у = -2х4 x = y4. у = 3х у = 3-х у = ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...Взаимное расположение графиков линейных функций.
Цели урока:. Выяснить зависимость расположения графиков линейных функций от значений k и b. Научиться по внешнему виду определять взаимное расположение ...Взаимное расположение графиков линейных функций".
"Числа не Боги, они не управляют миром, они показывают, как управляется мир". (поэт, гений немецкой литературы, Гёте). -2 2 5 1 -4 0. 3 6. 4 -1. -3. ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Взаимное расположение графиков линейных функций.
Цели урока. Цели: Рассмотреть разные случаи взаимного расположения графиков линейных функций. Научились распознавать взаимное расположение графиков ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Взаимное расположение графиков линейных функций.
Экспресс – опрос:. Какую функцию называют линейной? Что является графиком линейной функции? Какой формулой задаётся прямая пропорциональность? От ...Вектор решение задач
Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b. Тивякова Л.А. № 2 Выразить ...Асимптоты. Построение эскизов графиков
Определение: прямая вида x=a называется вертикальной асимптотой для y=f(x), если. 1. Определение: прямая вида y=b называется горизонтальной асимптотой, ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Конспекты
Действия с величинами. Соотношение цены, количества, стоимости. Решение задач, выражений
Автор: Енина Н.В. учитель начальных классов МКОУ НОШ №17 ст.Зольской,. . Ставропольский край. . Урок математики в 3-м классе. УМК «Гармония». ...Две основные задачи на дроби
. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Методическая разработка урока математики . ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Взаимное расположение графиков линейных функций
ПЛАН-КОНСПЕКТ УРОКА Конспект урока по теме: «Взаимное расположение графиков линейных функций». . ФИО (полностью). . Чичерова Татьяна ...Действия с составными именованными числами. Решение задач различного вида
Урок математики в 4 классе. . По программе «Школа 2100». Тема урока:. “Действия с составными именованными числами. Решение задач различного вида. ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Вычитание из чисел 8, 9. Решение задач
КРАСНОПАХАРЕВСКАЯ ООШ – ФИЛИАЛ МБОУ «НОВАДЕЖДИНСКАЯ СОШ». Урок математики для 1 класса по теме: «Вычитание из чисел 8, 9. Решение задач». . Автор: ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Взаимное расположение графиков линейных функций
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию