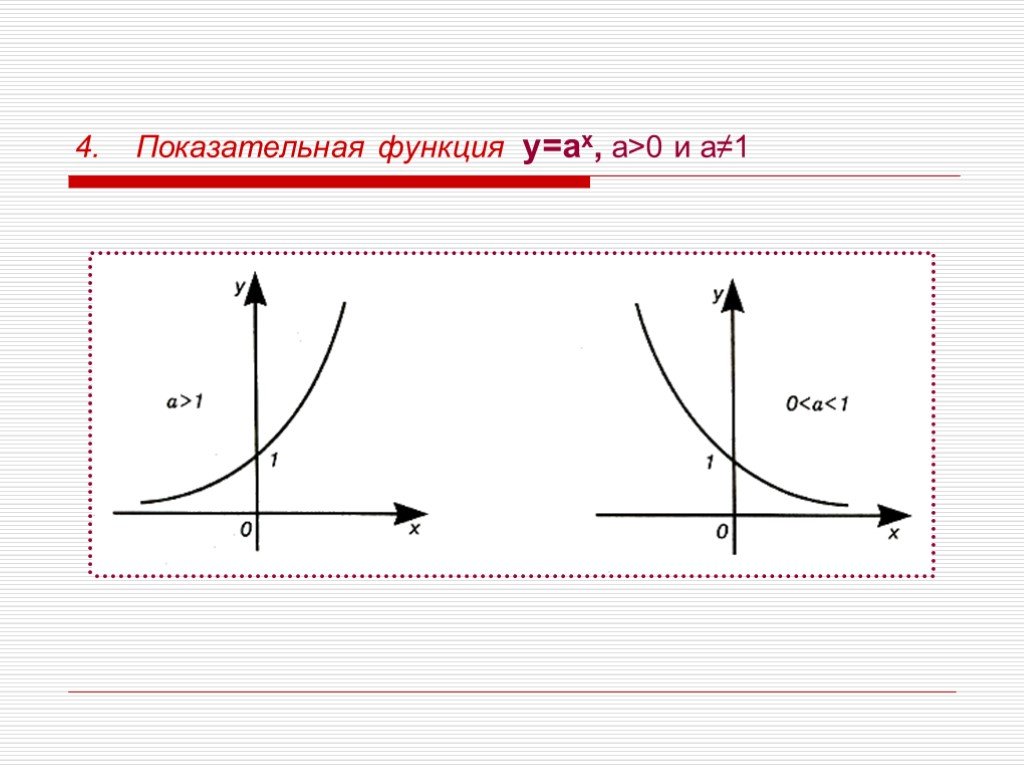
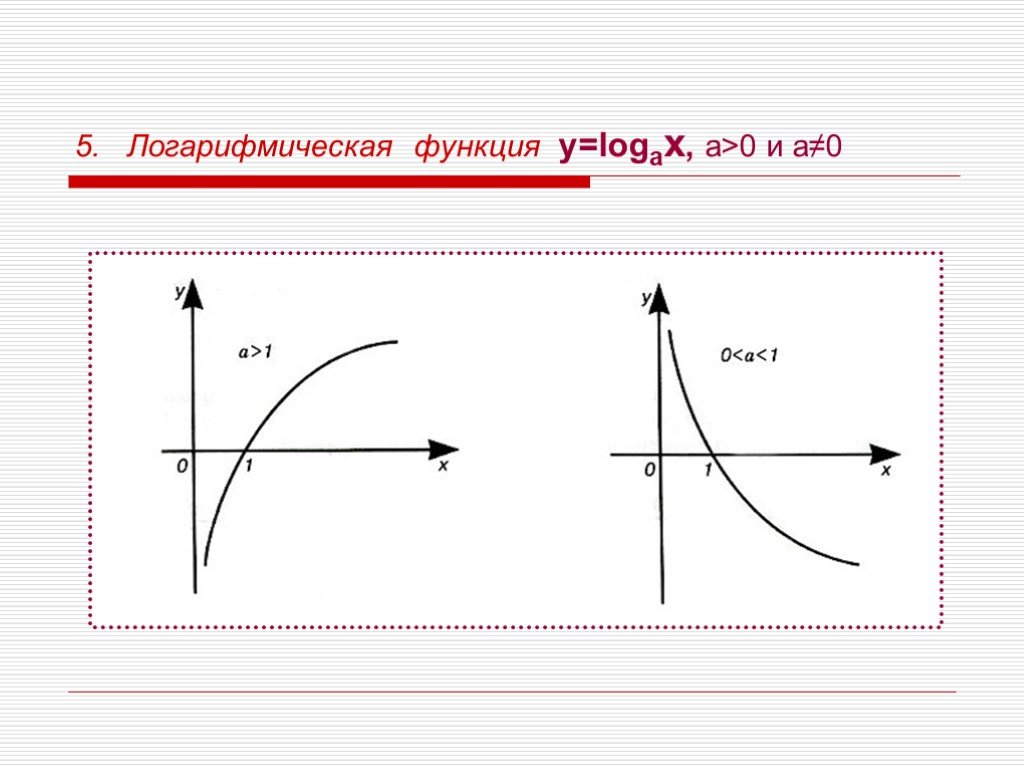
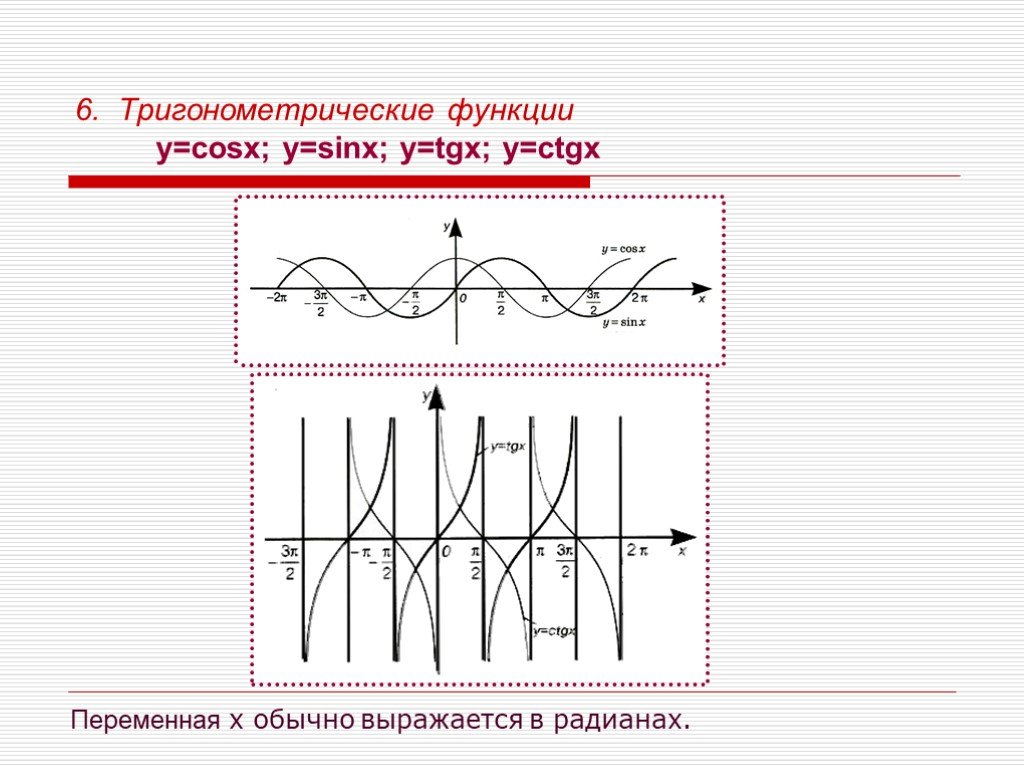
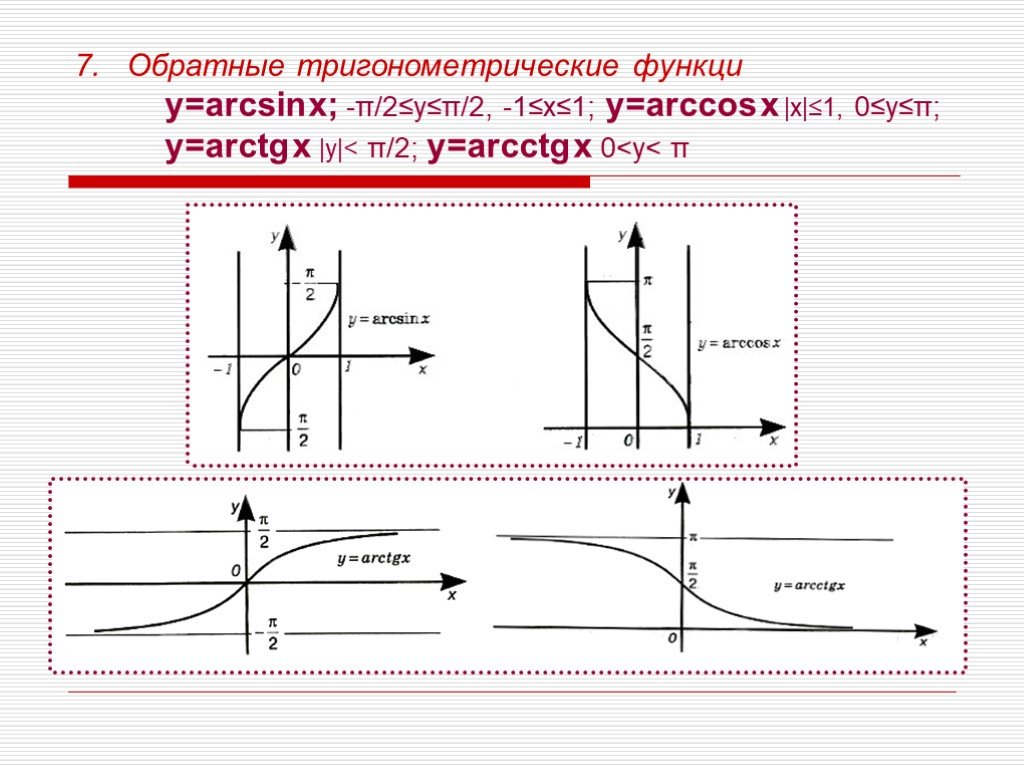
Презентация "Виды функций" по математике – проект, доклад
Презентацию на тему "Виды функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства функций
ОПРЕДЕЛЕНИЕ № 1. Функцию у = f(x) называют возрастающей на множестве X Є D(f), если для любых двух элементов x1 и х2 множества Х, таких, что x1 < ...Производная и графики функций
Доказать, что функция монотонна на заданном промежутке:. Дана непрерывная на функция. Используя график производной этой функции, определите, имеет ...Свойства обратных тригонометрических функций
Тема элективного занятия: «ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ. РЕШЕНИЕ УРАВНЕНИЙ, СОДЕРЖАЩИХ АРКФУНКЦИИ». ЦЕЛИ УРОКА: 1. Обобщить, систематизировать ...Преобразование графиков функций, содержащих модуль
y = f(x) + a y = f(x) y = f(x) - a +a -a. Преобразование графиков функций. Т1. Параллельный перенос по оси Оу. y = f(x) график исходной функции. y ...Применение производной к исследованию функций
Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики. Готфрид Вильгельм фон Лейбниц. ...Построение графиков функций, содержащих знак модуля
Содержание. I. Введение. II. Основная часть. 1) Понятия и определения. 2) Теоремы, следствия. 3) Построение графиков. III. Заключение. IV. Список ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Виды алгоритмов
Шевели мозгами! У Алёши а книг, у Бори b книг, а у Саши с книг. Что обозначают выражения? a + b b + c a + c a – b b – c a + b + c. 17.12.2017. Шевели ...Виды алгоритмов и их характеристика
1. Линейный алгоритм. Все действия выполняются последовательно друг за другом. начало ввод действия вывод. 2. Разветвляющийся алгоритм. Выполнение ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Виды аксонометрических проекций
Цеди урока : Образовательная: - познакомить с видами аксонометрических проекций; - научить выполнять простые геометрические построения с использованием ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Аппроксимация функций
Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции. Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени ...Трапеция. Виды трапеции
Трапеция. от греч. trapeza — стол. Трапеция буквально — «столик». Геометрическая фигура была названа так по внешнему сходству с маленьким столом. ...Виды алгоритмов и работа с ними
- линейные - разветвляющиеся - циклические. линейным. называется алгоритм, в котором действия выполняются после- довательно. например: режим дня. ...Угол. Виды углов (задания)
Отгадайте загадку. Здравствуйте, ребята! Меня зовут Сова – умная голова. Вместе с вами мы отправимся в замечательный город – Геометринск! Что ж пора ...Виды вкладов и расчет накоплений
Цель работы : развитие экономического образа мышления - умения применять аппарат математики и экономики для анализа конкретных экономических явлений ...Пределы последовательностей и функций
Цели:. Сформировать понятие предела последовательности, функции; Ввести понятие сходящихся и расходящихся последовательностей, горизонтальной асимптоты; ...Виды движения
Понятие движения. Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками. Примером движения могут служить: ...Конспекты
Применение производной для исследования функций на монотонность и экстремумы
Урок алгебры в 10 классе. по теме: «Применение производной для исследования функций. . на монотонность и экстремумы». Тип урока:. . интегрированный. ...Производные функций и применение производной
Государственное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа с. Чёрный Ключ. . муниципального района Клявлинский ...Нестандартные методы решения уравнений и неравенств. Использование области определения функций
Тема урока: Нестандартные методы решения уравнений и неравенств. Использование области определения функций. . ФИО (полностью). . Кривошеин ...Преобразование графиков тригонометрических функций
. . Воробьева Ирина Юрьевна. учитель математики. 1 категории. ГУ «Экономический лицей». г. Семей. Методическая разработка урока. ...Исследование взаимного расположения графиков линейных функций
МОУ ООШ с. Иран, учитель математики Джабиева Рита Алексеевна. . Пояснительная записка. Предмет:. алгебра. Класс:. 7. Тема:. «. Исследование ...Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений
Тема урока: Квадратные уравнения. Виды квадратных уравнений. Решение неполных квадратных уравнений. Цели урока:. Образовательные. :. . ...Взаимное расположение графиков линейных функций
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Треугольники. Виды треугольников: прямоугольный, остроугольный, тупоугольный и различение их на рисунках
Ф.И.О. . Михеенко Ольга Сергеевна,. . учитель начальных классов МОУ СОШ №70. Предмет:. математика. Класс:. 2 «А». Тип урока:. Изучение нового ...Взаимное расположение графиков линейных функций
Муниципальное образовательное учреждение средняя общеобразовательная школа № 33 с углубленным изучением отдельных предметов. Дзержинского района ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 апреля 2019
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию