Презентация "Свойства функций" по математике – проект, доклад
Презентацию на тему "Свойства функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Основные свойства функций
Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому ...Свойства и графики элементарных функций
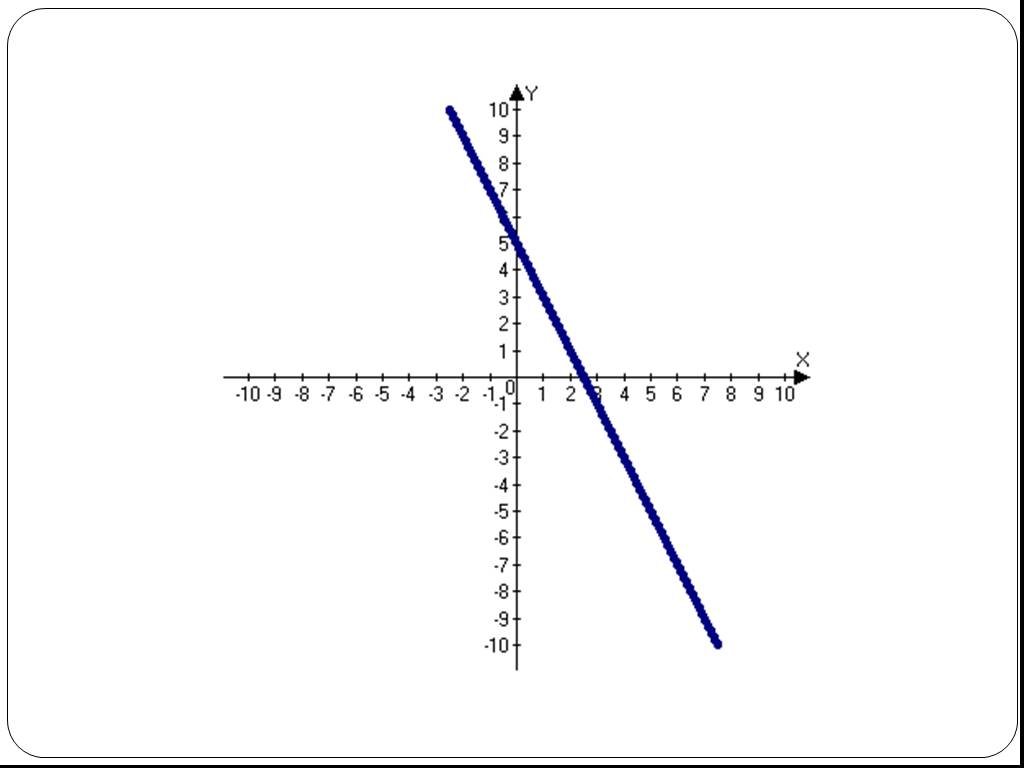
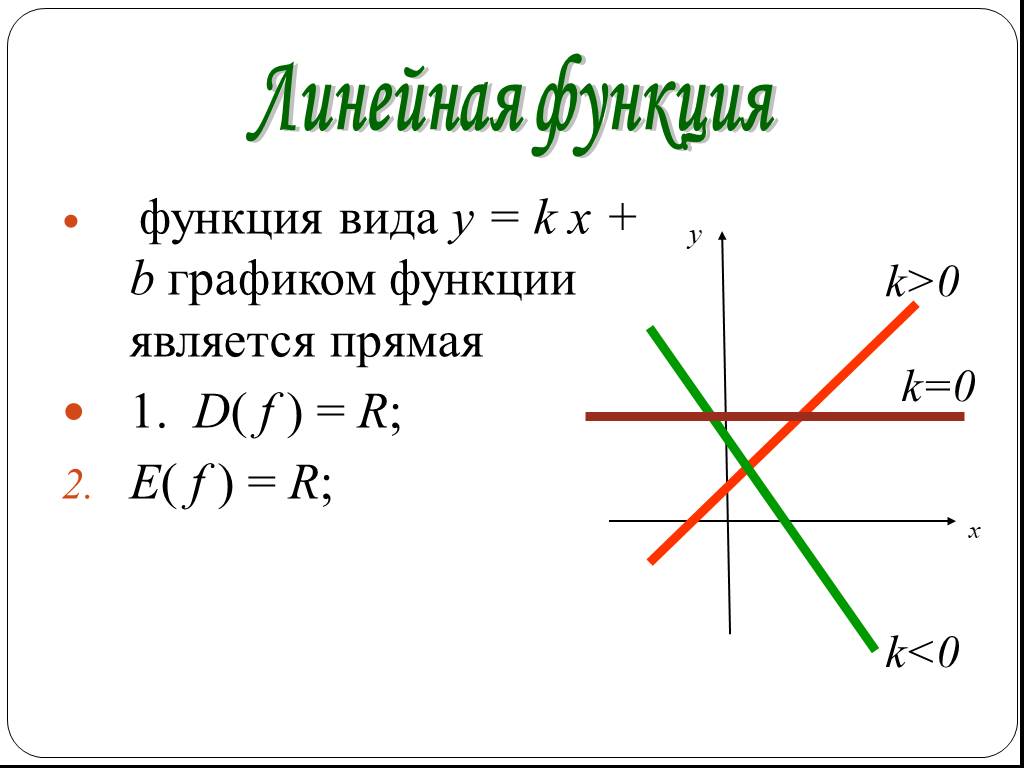
1. Определение функции. 2. Линейная функция: возрастающая; убывающая; частные случаи. 3. Квадратичная функция. 4. Степенная функция: с четным натуральным ...Свойства обратных тригонометрических функций
Тема элективного занятия: «ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ. РЕШЕНИЕ УРАВНЕНИЙ, СОДЕРЖАЩИХ АРКФУНКЦИИ». ЦЕЛИ УРОКА: 1. Обобщить, систематизировать ...Общие свойства функций
Вариант 1 Вариант 2 Задача 1. Найти область определения функции. Задача 2. Функция f(x) возрастающая. Сравните f(3) и f(5). Функция f(x) убывающая. ...Свойства производной. Построение графиков функций
Построение графика функции, заданной формулой, начинают с её исследования 1) Находят область определения функции 2) Выясняют, является ли функция ...Преобразования графиков функций
y=f(x) y=|f(x)| y=f(|x|) |y|=f(x) |y|=|f(x)| y=|f(|x|)|. Актуальность: Эта тема актуальна, т.к. в конце 11 класса необходимо сдавать единый государственный ...Свойства натурального ряда
ИССЛЕДОВАНИЕ. ИССЛЕДОВАНИЕ Предмет исследования. ИССЛЕДОВАНИЕ Предмет исследования Свойства натурального ряда. ИССЛЕДОВАНИЕ Предмет исследования Свойства ...Свойства и график логарифмической функции
- 5 - 4 - 3 - 2 -1 0 1 2 3 4 5 4 3 2 1 -1 -2 -3 -4. D(f)= E(f)= y=0 при х= y>0 при х y. Логарифмическая функция, её свойства и график. Опр. Логарифмической ...Свойства квадратного корня
ПЛАН УРОКА. 1.Организационный момент 2. Проверка домашнего задания 3. Устная работа 4. Закрепление изученного материала 5. Самостоятельная работа ...Свойства арифметического квадратного корня
Куда: г. Стерлитамак, МБОУ «СОШ №8» Кому: 8 классу. Прочитайте выражения:. х+75 (15-8)+у 34-(х+10) (а-12)-(х-86) (х-у)-(7+а) (у+99)+(76-4) (25+у)-х ...Готовимся к ОГЭ – 2018 Задание 23 Графики функций
Цель урока: подготовка к ОГЭ; отработка умений решать задачи, связанные с построением графиков различных функций. Постройте график функции и определите, ...Графики квадратичных функций
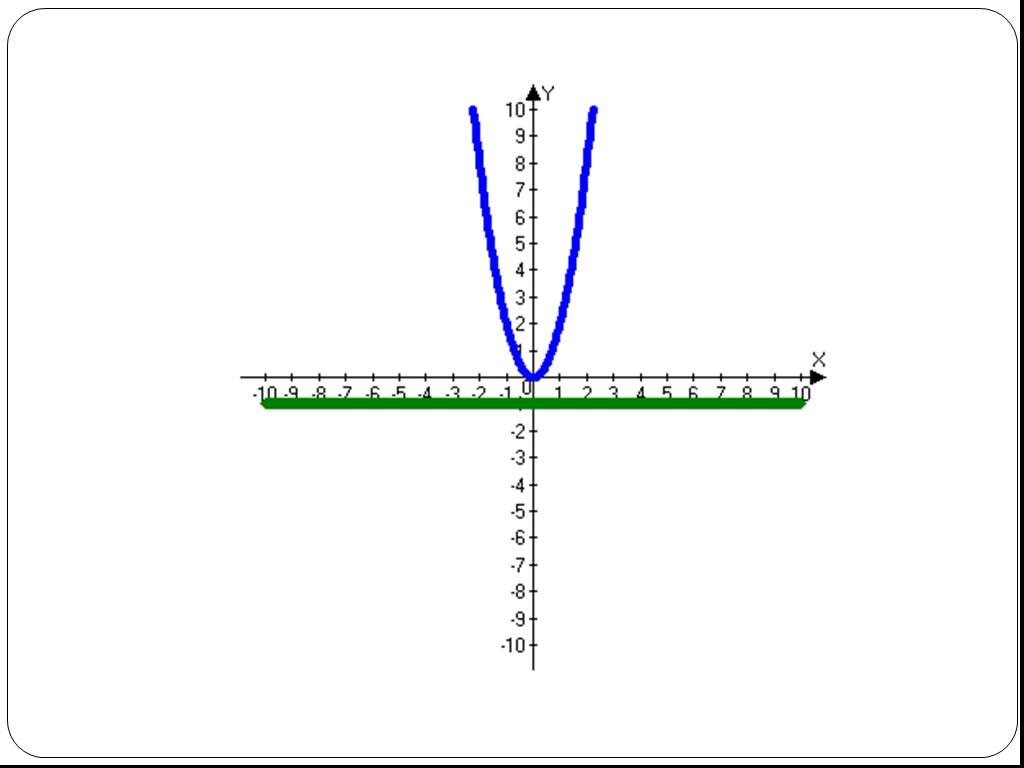
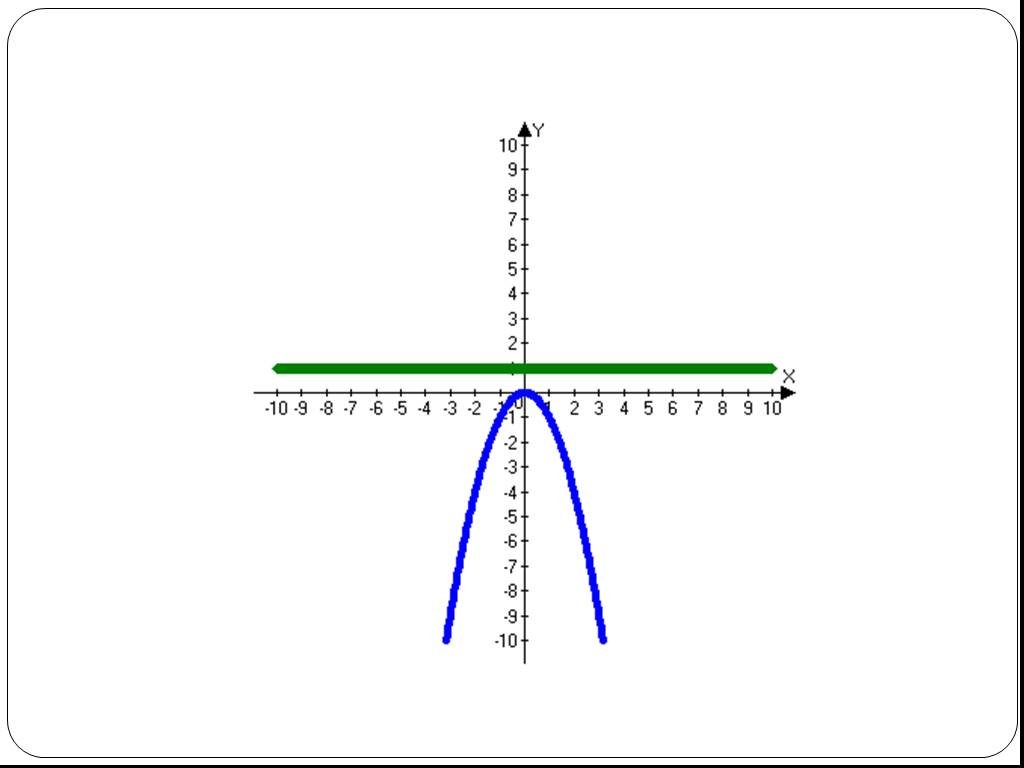
Этапы рассмотрения Простейшие примеры Свойства графиков квадратичных функций Графики и коэффициенты уравнений – простейшие закономерности Динамические ...Возрастание и убывание функций
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на отрезке [-1;10]. Эта функция ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Виды функций
План. Величины постоянные и переменные Понятие функции: определение функции область определения, значения сложная функция способы задания функции ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Алгоритм. Свойства алгоритма
Алгоритм «Заваривания чая». Вскипятить воду. Окатить заварочный чайник кипятком. Засыпать заварку в чайник. Залить кипятком. Закрыть крышечкой. Накрыть ...Графики простейших функций, содержащих модули
Графики простейших функций, содержащих модули. Определение модуля:. Модулем числа х называется расстояние от начала отсчета до точки, изображающей ...Конспекты
Свойства функций
МОУ «Никифоровская СОШ №2». . Интегрированный урок алгебра – ИВТ с использованием слайдов. ...Свойства функций. Чтение графиков функций
Муниципальное бюджетное образовательное учреждение «Усть – Вельская СОШ № 23». Свойства функций. Чтение графиков функций. Конспект урока по алгебре. ...Свойства функций
Конспект урока по алгебре и началам анализа в 11 классе. . . . Учитель математики высшей категории. Юдинцева Валентина ...Свойства функций
Тема урока:. Свойства функций. Предварительная подготовка к уроку:. обучающиеся должны знать следующие темы: «Линейная функция и ее график», «Обратная ...Свойства функций
Урок по теме:. Свойства функций. . 9 класс ,алгебра. Подготовила учитель. МОУ СОШ№1. Дмитренко В.А. Цель урока. : «Совершенствовать навыки ...Решение уравнений нестандартными методами, используя свойства функций
Подготовил и провел учитель математики. . МКОУ «СОШ №1» г. Поворино. . Воронежской области. . Карташова С. А. 2014г. Тема урока:. ...Применение свойства монотонности функций при решении уравнений и неравенств
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Свойства тригонометрических функций
Тема: Свойства тригонометрических функций. Цель:. Повторить, закрепить, обобщить свойства тригонометрических функций. Совершенствовать умения и ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Свойства предметов. Выделение из группы предметов одного или нескольких предметов, обладающих определёнными свойствами
МКС(К)ОУ "Краснинская школа - интернат. VIII. вида". Конспект урока по математике. «Свойства предметов. Выделение из группы предметов ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 мая 2019
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию














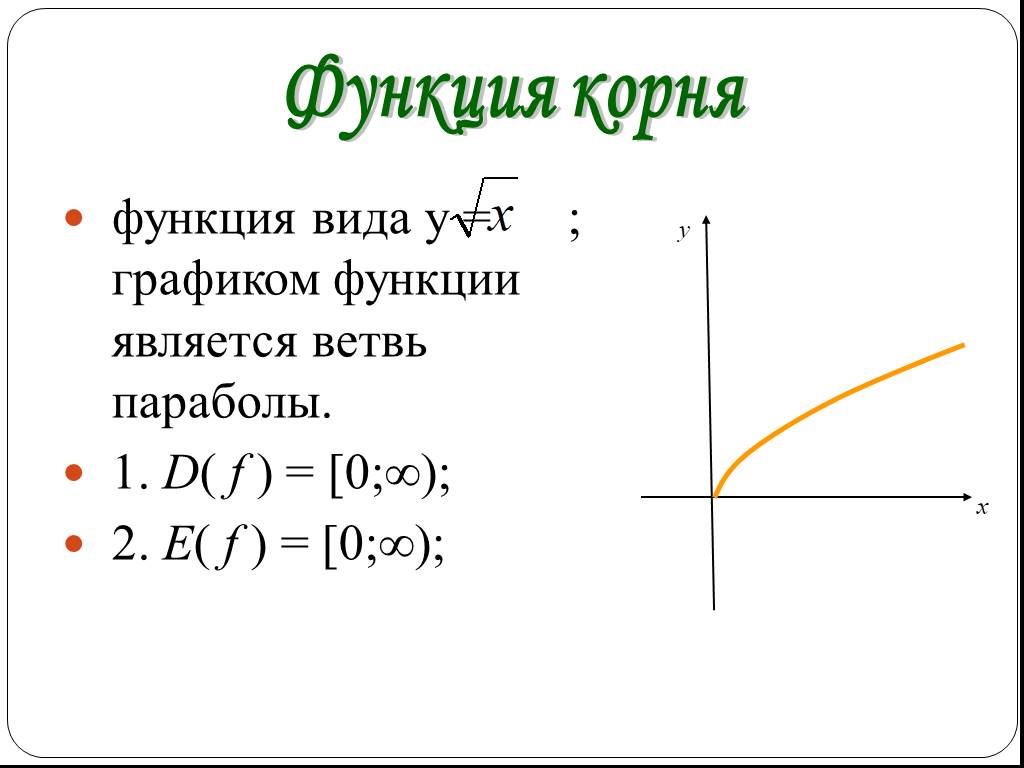














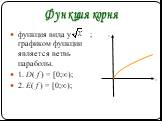
![функция вида y = |x|; 1. D( f ) = R; 2. E( f ) = [0;∞); 3. график функции на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х. Функция модуля функция вида y = |x|; 1. D( f ) = R; 2. E( f ) = [0;∞); 3. график функции на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х. Функция модуля](https://prezentacii.org/upload/cloud/19/05/146575/images/thumbs/screen20.jpg)