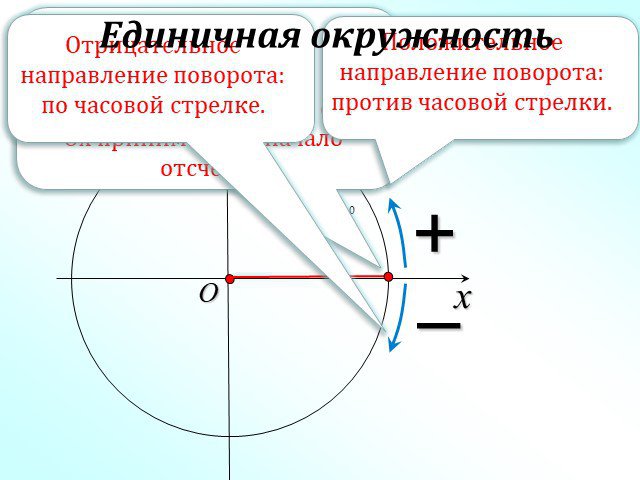
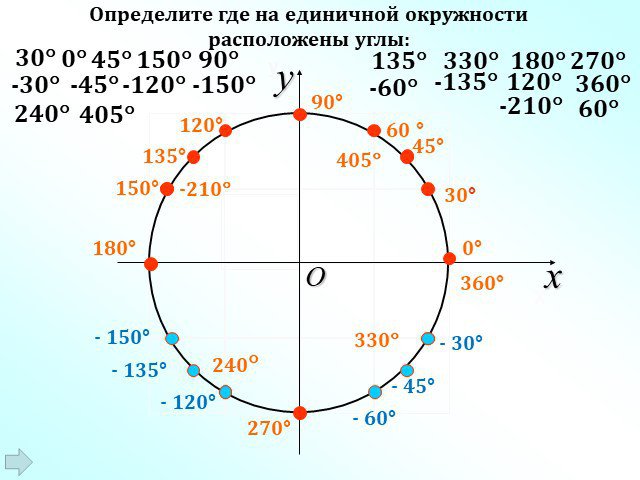
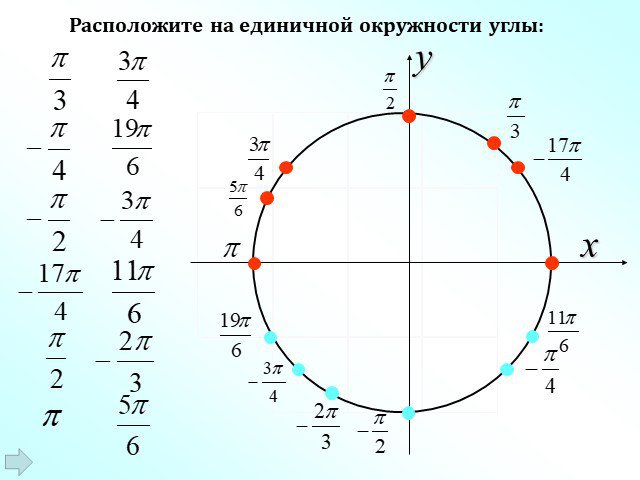
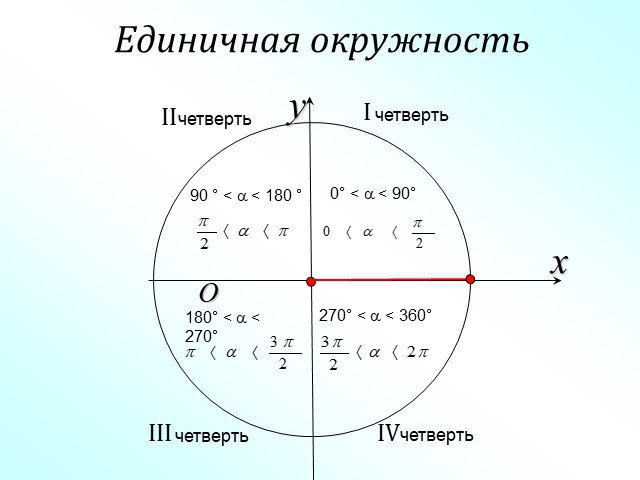
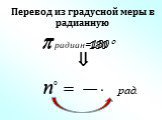
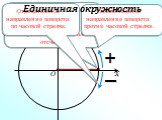
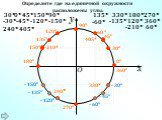
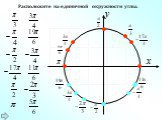
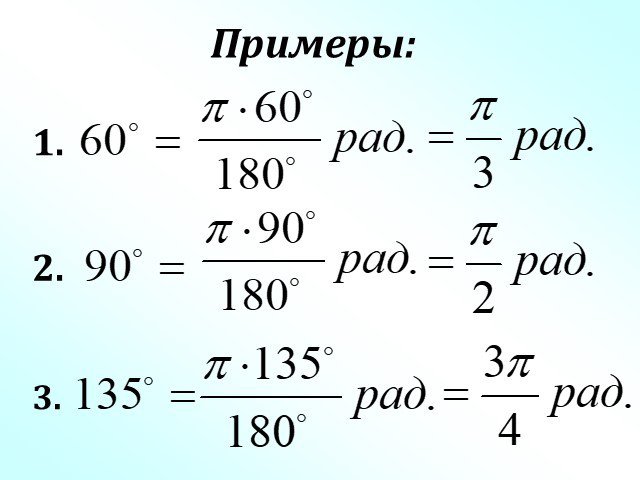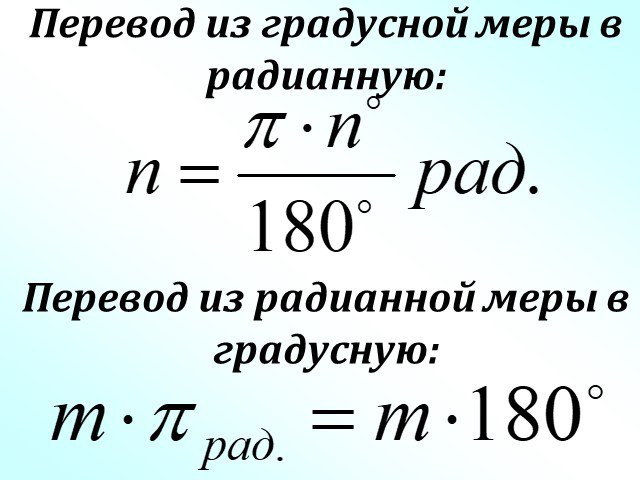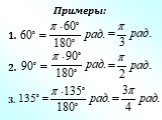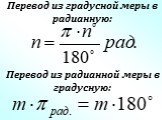Презентация "Радианная мера угла. Угол поворота" (10 класс) по математике – проект, доклад
Презентацию на тему "Радианная мера угла. Угол поворота" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
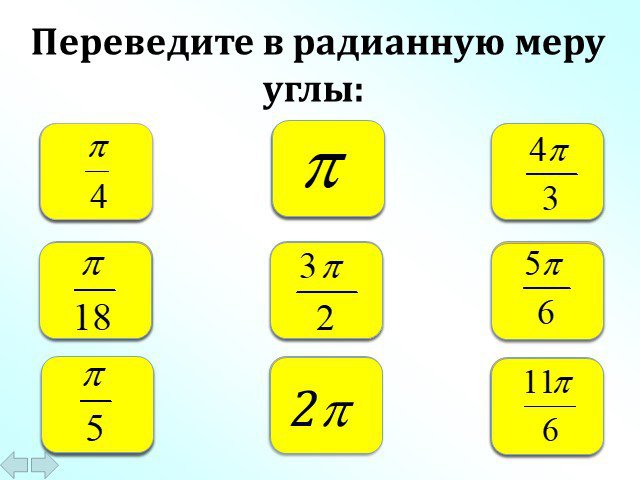
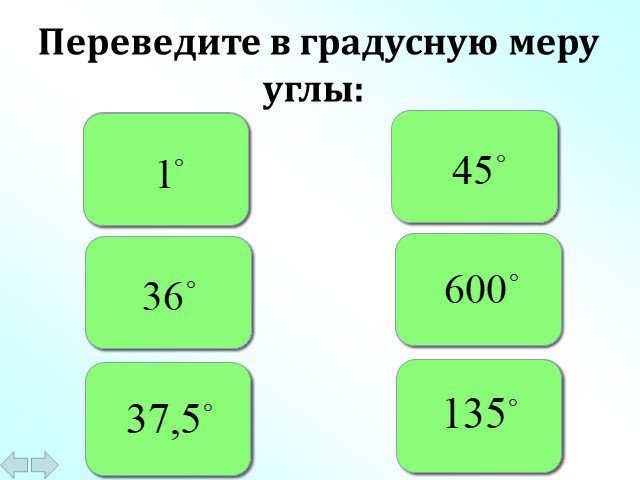
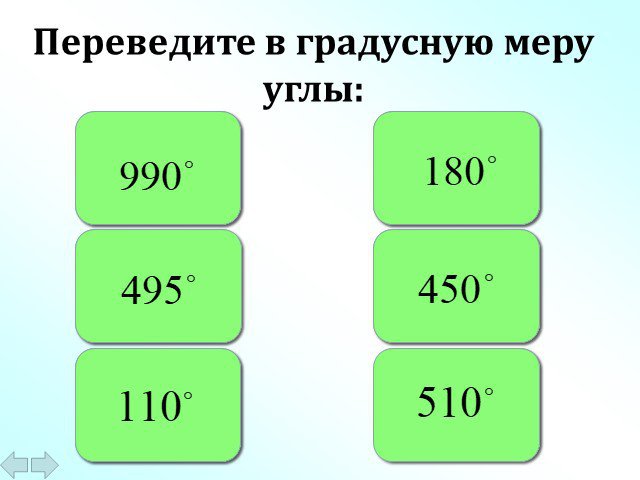
Слайды презентации
Список похожих презентаций
Косинус острого угла прямоугольного треугольника
Историческая справка. Расположение углов и сторон. А С В b c a. АС – противолежащий катет. ВС – прилежащий катет. ВС - противолежащий катет. АС – ...Биссектриса угла в треугольнике
Задачи УЧЕБНИК А О В С D 80º ? 180º- 80º= 100º 100º Ответ:155º, 25º, 155º. Задача №535 биссектриса ? Определение. Биссектриса угла – это луч с началом ...Косинус угла
О В А С D. М N C. . Треугольник АВС – прямоугольный. ∟С – прямой. ∟А – острый. АС - прилежащий катет. ВС – противолежащий катет. АВ – гипотенуза. ...Золотое сечение - божественная мера красоты
Предмет исследования: элементы, связанные друг с другом золотой пропорцией, большинству людей кажутся красивыми, такая пропорция создает зрительное ...Знаменитые задачи древности. Трисекция угла
Выполнил: ученик 6 класса Зеленин Никита Руководитель: учитель математики Левищенко О. П. Образовательное учреждение: МОУ «Средняя общеобразовательная ...Задача о трисекции угла
Задача о трисекции угла разрешима при некоторых частных значениях величины данного угла. A C N M B D. При помощи циркуля и линейки можно разделить ...Cинус, косинус, тангенс и котангенс угла
Тест. Синус угла А равен: а) 4/5; б) 3/5; в) 4/3 2.Тангенс угла В равен: а) 4/3; б) 3/5; в)¾ 3.Косинус. равен : а) б) ½; в). 4. Упростить выражение:. ...Перпендикуляр и наклонная. Угол между прямой и плоскостью.
Перпендикуляр и наклонная. 1.Перпендикуляр МН – отрезок прямой, перпендикулярной к прямой a, проходящей через точку М. MН – перпендикуляр к прямой ...Двугранный угол. Угол между плоскостями
Основные понятия. Прямая а разделяет плоскость на две полуплоскости. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями ...Величина двугранного угла
?. ПОВТОРЕНИЕ ( устная работа). 1) Что называется углом на плоскости? 2) Какой угол называется углом между прямыми в пространстве? 3) Какой угол называется ...Божественная мера красоты
Что общего? Последовательность Фибоначчи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится».. Кто-то поместил пару кроликов ...Биссектриса угла
Цели:. Повторить с учащимися определение смежных углов, вертикальных углов, теорему о смежных углах, вертикальных углах. Ввести определение биссектрисы, ...Определение синуса, косинуса, тангенса и котангенса углов поворота
x y 1 0. Вспомним, что любая точка координатной плоскости имеет две координаты – абсциссу и ординату:. y – ордината точки M. x – абсцисса точки M. ...Двугранный угол. Угол между плоскостями2
В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD. В правильной пирамиде SABCD, все ребра которой равны 1, найдите ...Определение угла
Класс: 7 «А» Дата: ноябрь 2010 года Предмет: геометрия Тип урока: объяснение нового материала Тема урока: «Первые уроки геометрии. Углы» Форма урока: ...Зависимость между синусом, косинусом и тангенсом одного и того же угла
∙. . . П р о в е р ь и о ц е н и с е б я ! Ордината Абсцисса. О с н о в н о е т р и г о н о м е т р и ч е с к о е т о ж д е с т в о :. a2-b2=(a-b) ...Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку ..."Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ...Конспекты
определение угла
Конспект занятия (при реализации классно-урочной системы обучения). Учитель математики МОУ «»Сторожевская СОШ» Латкина Надежда Анатольевна. Тема ...Величина угла
Тема: Угол. Величина угла/1/. Цель урока:. -. образовательная. : способствовать совершенствованию полученных знаний по применению и развитию при ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:21 марта 2017
Категория:Математика
Классы:
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию