Презентация "Божественная мера красоты" по математике – проект, доклад
Презентацию на тему "Божественная мера красоты" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 43 слайд(ов).
Слайды презентации
Список похожих презентаций
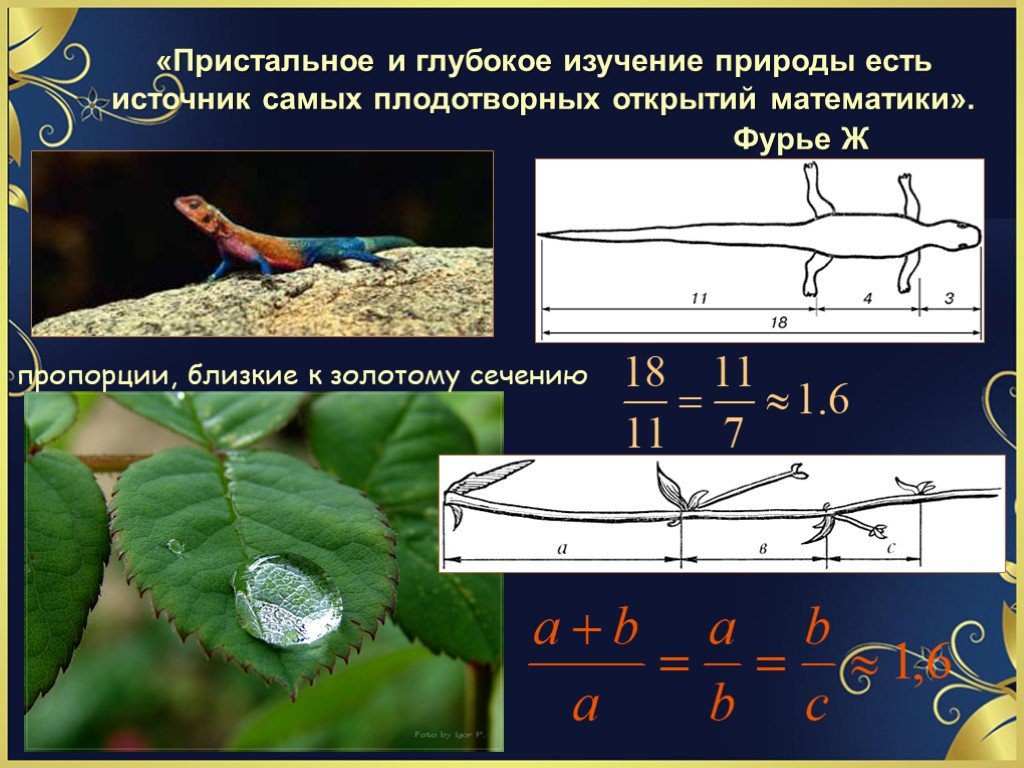
Золотое сечение - божественная мера красоты
Предмет исследования: элементы, связанные друг с другом золотой пропорцией, большинству людей кажутся красивыми, такая пропорция создает зрительное ...Угол поворота. Радианная мера угла
Проверка домашней работы. Устный счет. Найдите градусную меру угла. π 2π 450 900 180 1800 3600. Найдите радианную меру угла. 900 1800 3600 180. 2π ...Угол поворота. Радианная мера угла
Укажите соответствие:. 1 3 4 5. развёрнутый угол прямой угол тупой угол полный угол острый угол. Угол поворота х у -1 II IV I III. ОР0 - неподвижный ...Русская мера веса
ФУНТ (от латинского слова 'pondus' - вес, гиря) равнялся 32 лотам, 96 золотникам, 1/40 пуда, в современном исчислении 409,50 г. Используется в сочетаниях: ...Радианная мера углов и дуг
Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад). 1 рад R A B O ...Радианная мера угла. Угол поворота
Угол – геометрическая фигура, состоящая из двух лучей, выходящих из одной точки. α. Измерение углов . Единицы измерения угла: 1 минута ( 1’) - 1 ...Радианная мера угла
Каждой точке прямой ставиться в соответствие некоторая точка окружности. Точки (1, π/2, -1, -2) перейдут соответственно в точки окружности (М1, М2, ...Радианная мера угла
1 1 радиан. Угол в 1 радиан – это центральный угол окружности, который соответствует дуге, равной радиусу. № 1.2.1. № 1.2.2. № 1.2.3. № 1.2.4. Точки ...Орнамент - математическое воплощение красоты
Цель: Продемонстрировать возможности законов геометрии при создании различных орнаментов, украшающих многие предметы декоративно-прикладного искусства. ...Математический закон красоты мира
Гипотеза: Я предполагаю, что красота мира подчиняется какому – либо математическому закону. Цель исследования: Вывести закон красоты мира с точки ...Математика и архитектура
Ни один из видов искусств так тесно не связан с геометрией, как архитектура. «Окружающий нас мир – это мир геометрии чистой, истинной, безупречной ...Золотое сечение и числа Фибоначи
. 1+1=2 1+2=3 2+3=5 3+5=8 5+8=13 8+13=21 13+21=34 21+34=55 34+55=89 55+89=144. 13:8=1,625 21:13=1,615… 55:34=1,617.. 144:89=1,6179… 610:377=1,618. ...Золотое сечение на Новгородчине
Цель данной работы: формирование представлений о “золотом сечении”, как основе пропорционального строя архитектурных шедевров. Задачи данной работы: ...Золотое сечение или гармоническая пропорция
Учебный проект по математике. Автор проекта: Урбаева Клара Климентьевна, зам. директора ОГОУ НПО ПУ № 59 по общеобразовательным дисциплинам, преподаватель ...Золотое сечение вокруг нас
Актуальность. 1. Увлекательная история «Божественной пропорции» 2.Всеобщий характер исследуемого материала 3.Познание законов гармонии и красоты. ...Золотое сечение и применение золотого сечения в жизни
Цель работы:. 1.Изучить тему «золотая пропорция». 2.Рассмотреть связанные с нею отношения. 3.Познакомиться с «золотой пропорцией» в природе. Методы ...Золотое сечение в математике
Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе ...Золотое сечение в математике и в жизни
« В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценность золота, ...Золотое сечение в геометрии
Правило Золотого Сечения впервые сформулировано Евклидом. Вкратце оно определяется так: отношение целого к большей части должно равняться отношению ...Конспекты
Радианная мера угла
Республика Казахстан. г. Шымкент. основная школа № 112. имени Б.Садыкова. учитель математики. . Адилметов Мирахмат Сулайманкулович. Предмет:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 декабря 2018
Категория:Математика
Содержит:43 слайд(ов)
Поделись с друзьями:
Скачать презентацию