Презентация "Золотое сечение и применение золотого сечения в жизни" по математике – проект, доклад
Презентацию на тему "Золотое сечение и применение золотого сечения в жизни" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
"Золотое сечение".
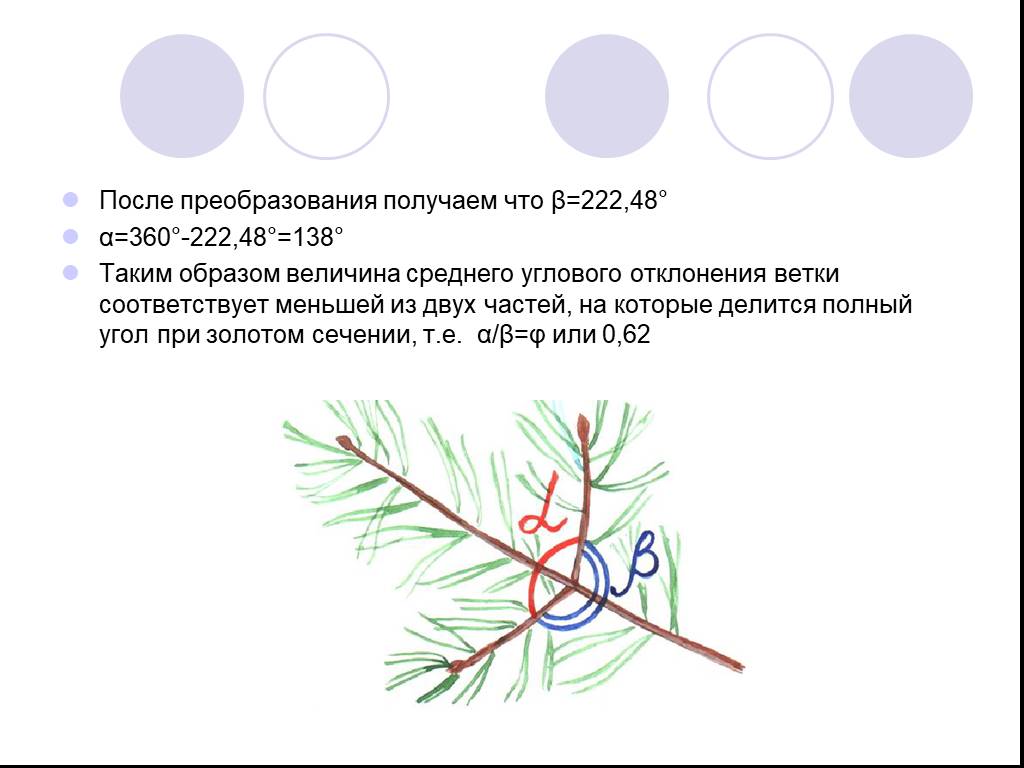
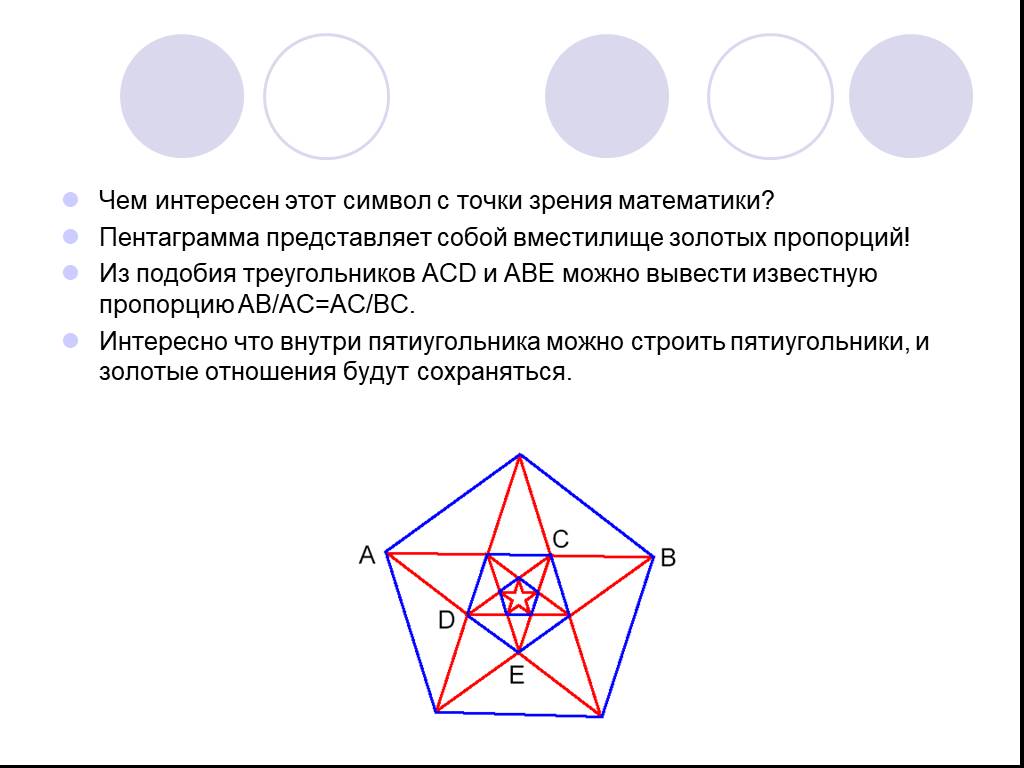
Золотое сечение. божественная золотая золотое сечение золотая середина золотое деление золотое число. Золотым сечением называют деление отрезка, при ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ..."Симметрия в архитектуре Старого Оскола"
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ..."Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...«Правильные и неправильные дроби»
«Учёные Грузии нашли золото в составе крови человека». Из журнальной статьи. “ЗОЛОТАЯ КРОВЬ” (ЭДУАРД АСАДОВ). Не так давно учёные открыли Пусть небольшой, ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ...5.Уравнение в полных дифференциалах. Интегрирующий множитель
Теорема:. Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Сложение и вычитание десятичных дробей»
Чтобы сложить (вычесть) десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы ...I Функция У=АХ², её график и свойства
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...Конспекты
I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. ...Арифметический квадратный корень и его свойства
Тема: «Арифметический квадратный корень и его свойства». Урок-игра «Аукцион математических знаний». Цели урока. :. . Образовательные:. - ...Веселая и полезная математика
. Тюрина Валентина Викторовна. 1 квалификационная категория – учитель математики. Город Прокопьевск Кемеровская область. МКОУ «Школа – интернат ...Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов
Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов. . КАЗАХСТАН. ЮЖНО-КАЗАХСТАНСКАЯ ОБЛАСТЬ. Г.ШЫМКЕНТ, ОСНОВНАЯ СРЕДНЯЯ ШКОЛА №97. ...+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при ...Вероятность и математическая статистика
Открытый урок. . по учебной дисциплине Теория вероятностей и математическая статистика. Тема: «Вероятность и математическая статистика». Группа ...Арифметический корень натуральной степени и его свойства
Урок алгебры в 9 классе. . Тема урока. : «Арифметический корень натуральной степени и его свойства». . Из опыта работы учителя математики. ...Арифметический квадратный корень из произведения, степени и дроби
Тема: «Арифметический квадратный корень из произведения, степени и дроби». Цели урока:. . Образовательные:. изучить основные свойства квадратных ...Верно и неверно
МБОУ Чымнайская средняя общеобразовательная школа имени Г.Д.Бястинова. Таттинского улуса республики Саха(Якутия). Варламова Татьяна Спиридоновна- ...Арифметический способ отбора корней в тригонометрических уравнениях
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях». Цели и задачи урока:. . . повторение ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 февраля 2019
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию