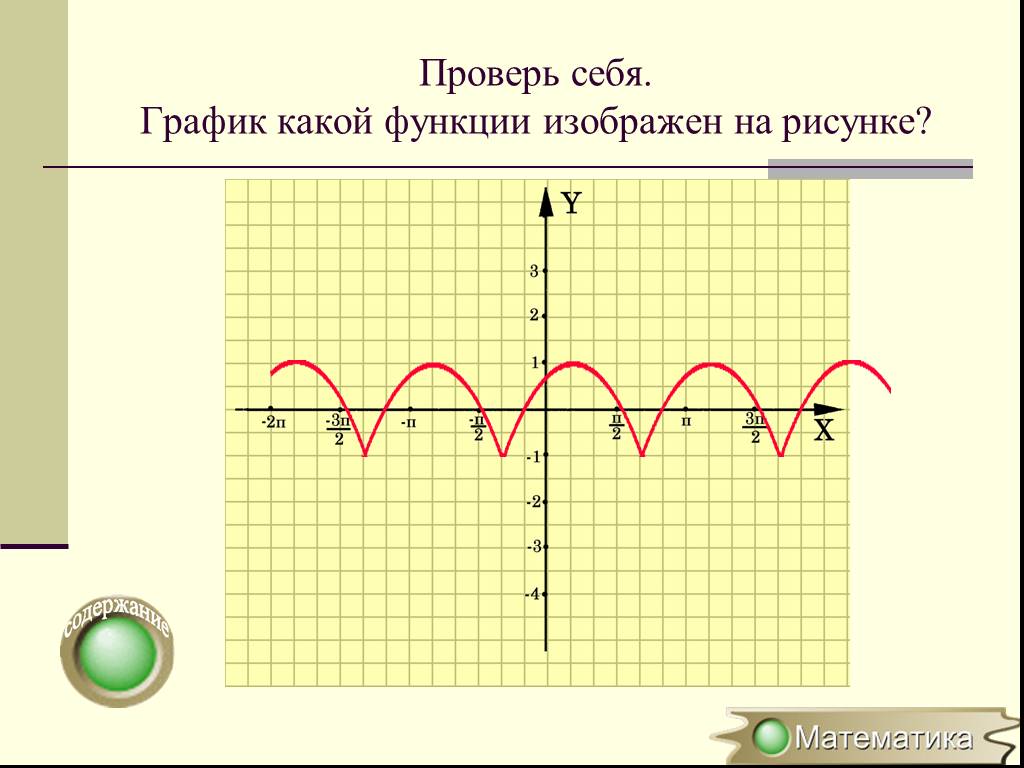
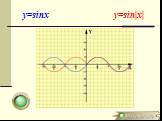
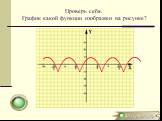
Презентация "Преобразование графиков" по математике – проект, доклад
Презентацию на тему "Преобразование графиков" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
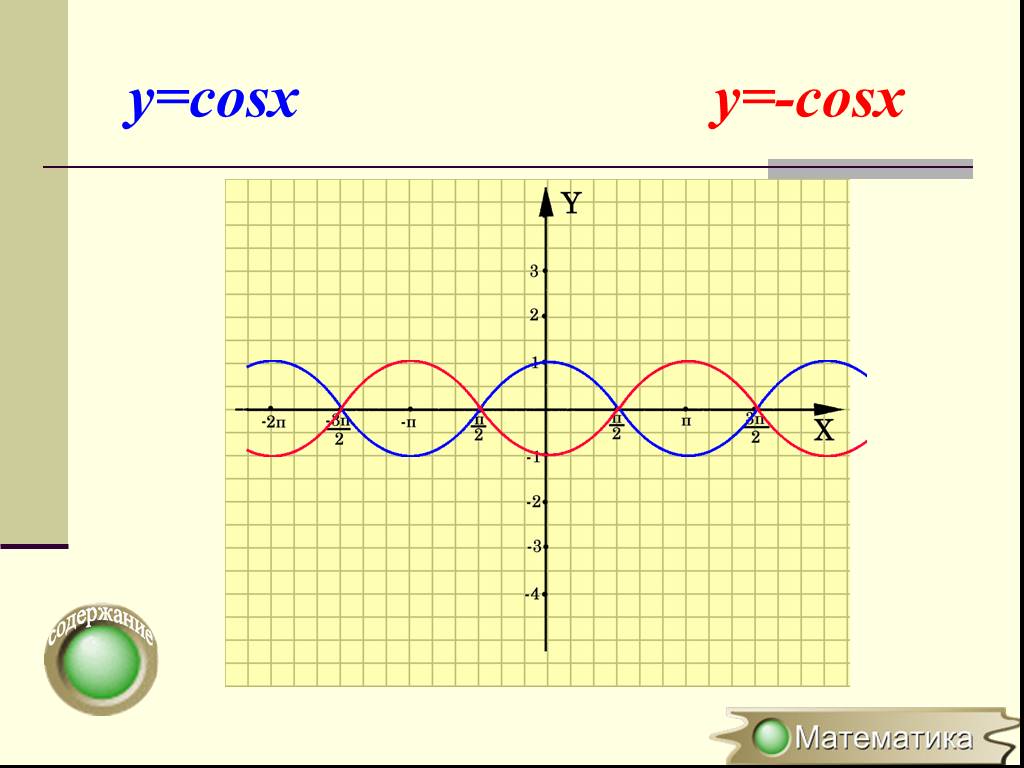
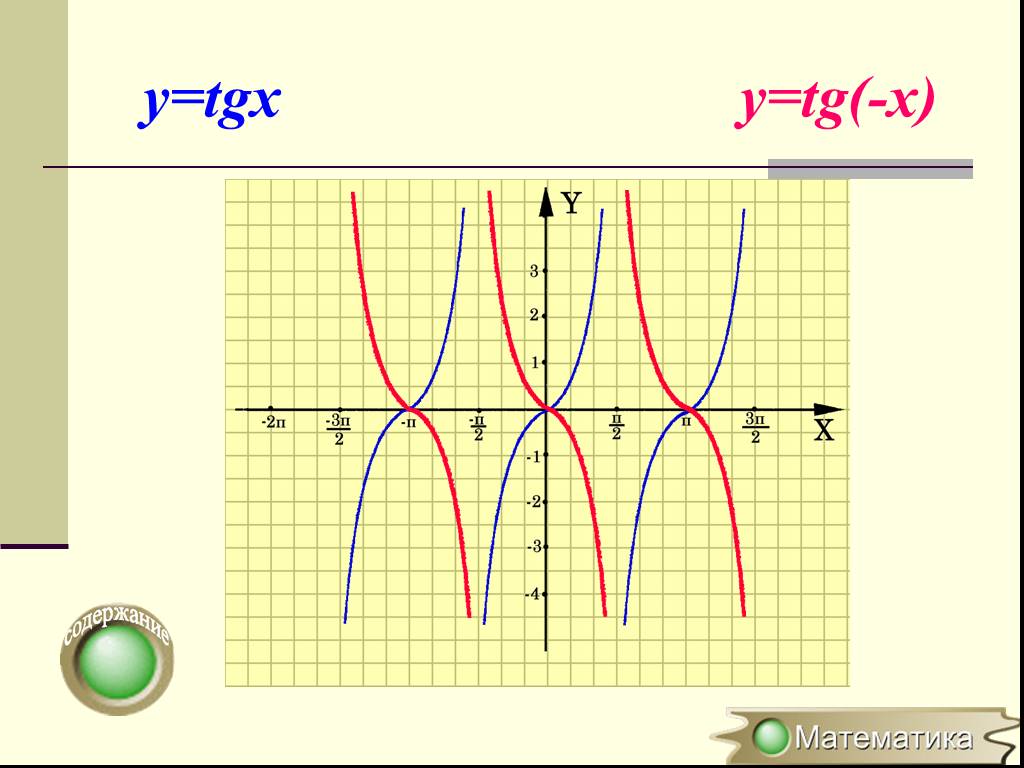
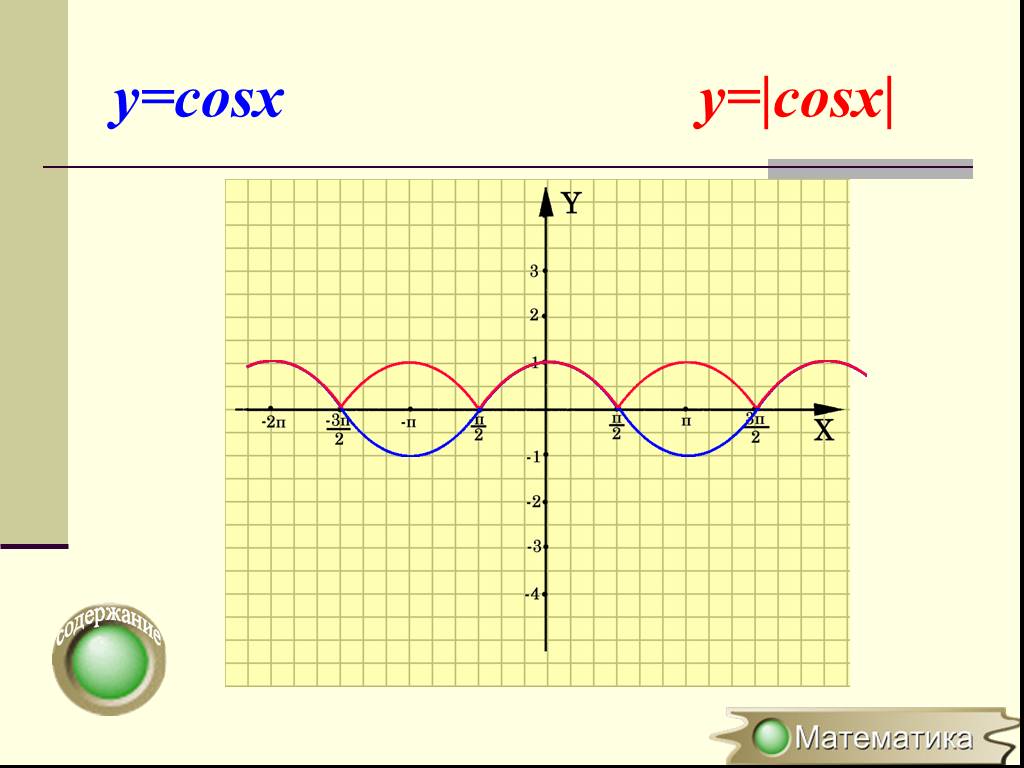
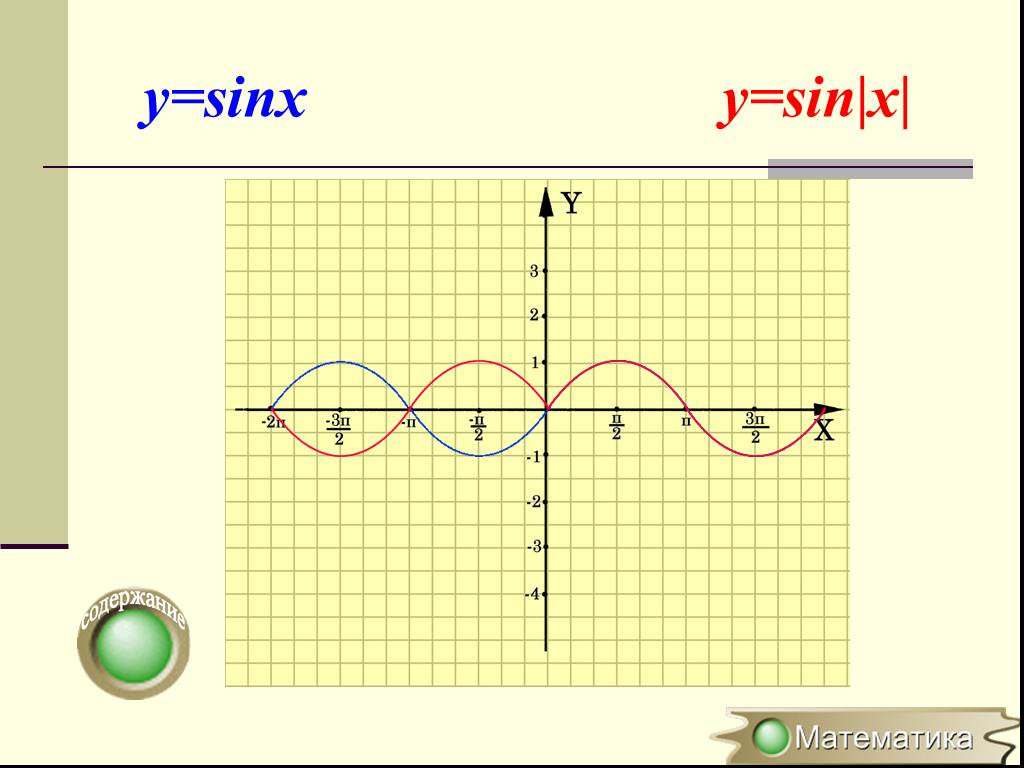
Преобразование графиков тригонометрических функций
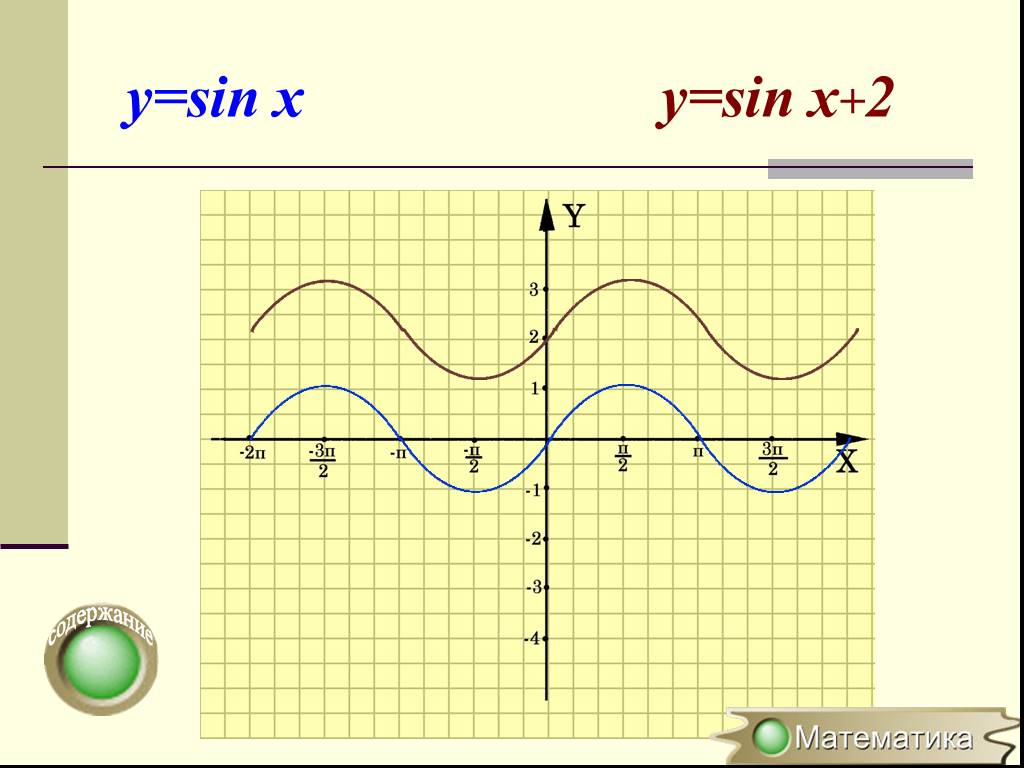
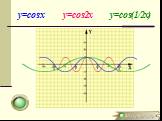
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Преобразование графиков тригонометрических функций
Цели урока:. Обобщить и систематизировать знания учащихся по теме. Показать актуальность темы в связи с введением ЕГЭ в штатный режим. Показать возможности ...Преобразование графиков тригонометрических функций
Цель урока:. Повторить свойства тригонометрических функций Изучить графическую программу Advanced Grapher, облегчающую построение графиков Изучить ...Преобразование графиков функции
Повторение. Как построить график функции если известен график функции. . Рассмотрим построение графика функции. 1 случай: m – положительное число. ...Преобразование графиков тригонометрических функций
Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в положительном направлении ...Преобразование графиков функций
Основные правила преобразования графиков функций. 1. У = - f(x) ← y = f(x) , отображением относительно оси ОХ. 2. У = f(- x) ← y = f(x), отображением ...Преобразование графиков функций
Дорогу осилит идущий, а математику – мыслящий Т.Эдисон. Цель урока. Изучить способ построения графиков функций y = f(kx), y = mf(x). Преобразование: ...Преобразование графиков функций
Y=f (x ). Y=f (x+c). c>0 Сдвиг по оси Ох на с единиц влево. Y= f(x+c). c. Y=f (ax). 0. Y=f(ax). a>1 Сжатие вдоль оси Ох в а раз (или к оси Оу). Y=f ...Преобразование графиков функций на координатной плоскости
Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...Преобразование графиков функций, содержащих модуль
y = f(x) + a y = f(x) y = f(x) - a +a -a. Преобразование графиков функций. Т1. Параллельный перенос по оси Оу. y = f(x) график исходной функции. y ...Преобразование графиков тригонометрических функций
Оборудование урока: компьютер, проектор, экран. Цели: Обобщить знания и умения. Развить умение наблюдать, сравнить, обобщать. Воспитать познавательную ...Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.
1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...Симметрия функций и преобразование их графиков
ЦЕЛИ:. Повторить определение функции; основные понятия, связанные с ней; способы задания функции. Ввести понятие чётной и нечётной функции. Освоить ...Преобразование тригонометрических графиков
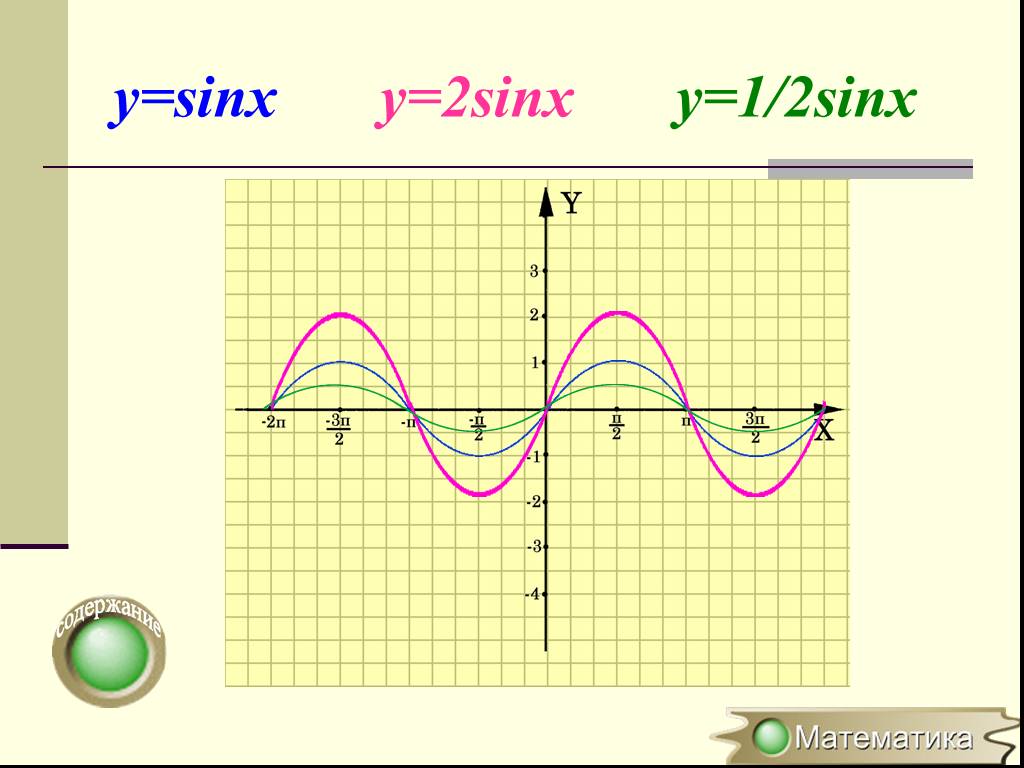
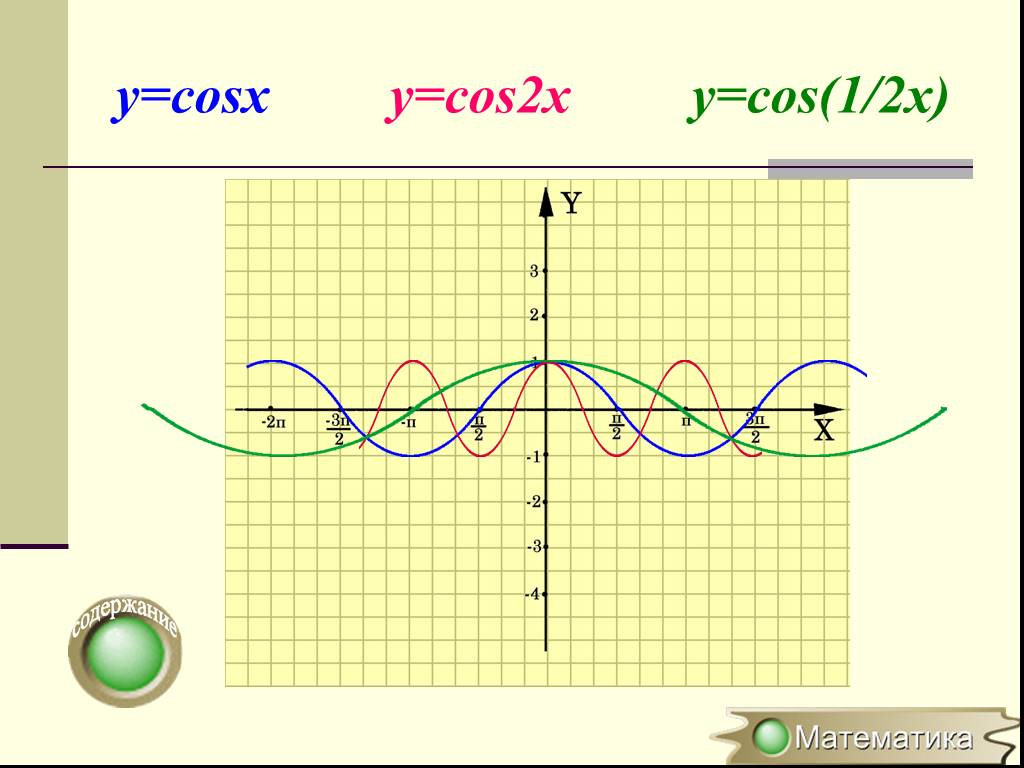
Характеристика преобразований графиков функций у=mf(x), y=f(kx) из графика функции y=f(x). 1. Если известен график функции y=f(x), то график функции ...Взаимное расположение графиков линейных функций.
Экспресс – опрос:. Какую функцию называют линейной? Что является графиком линейной функции? Какой формулой задаётся прямая пропорциональность? От ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Преобразование выражений, содержащих операцию извлечения квадратного корня
Основные свойства квадратного корня из неотрицательного числа. ? Тема:Преобразование выражений, содержащих операцию извлечения квадратного корня. ...Преобразование выражений, содержащих квадратные корни
Фронтальный опрос. Дайте определение арифметического квадратного корня. Перечислите свойства арифметического квадратного корня. Чему равно значение ...Свойства производной. Построение графиков функций
Построение графика функции, заданной формулой, начинают с её исследования 1) Находят область определения функции 2) Выясняют, является ли функция ...Зачем нужно строить асимптоты графиков дробно-рациональной функции?
В работе сделан экскурс в историю возникновения понятия асимптоты, сделан сравнительный анализ различных определений асимптоты. Рассматривается построение ...Конспекты
Преобразование графиков тригонометрических функций
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Преобразование графиков тригонометрических функций
. . Воробьева Ирина Юрьевна. учитель математики. 1 категории. ГУ «Экономический лицей». г. Семей. Методическая разработка урока. ...Преобразование графиков тригонометрических функций
Конспект урока по алгебре в 10 классе. Васильева Екатерина Сергеевна. ,. . учитель математики. ОГБОУ «Смоленская специальная (коррекционная). ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Преобразование рациональных выражений
Тема:. Урок- обобщение «Преобразование рациональных выражений». Цель:. Проверить знания уч – ся, умение выполнять действие с алгебраическими дробями. ...Преобразование дробно-рациональных выражений
Урок по теме:. . "Преобразование дробно-рациональных выражений". Капацына Людмила Константиновна,. учитель математики. . 1 категории,сшл№23 г.Актобе. ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Применение производной к исследованию функций и построению графиков
ОГБОУ СПО «Белгородский строительный колледж». Конспект урока по дисциплине. «Математика». Тема: «Применение производной к ...Преобразование целых выражений
Тема:. Преобразование целых выражений. Тип:. Повторения и обобщения материала. Цели:. 1.- Закрепить навыки преобразования целых выражений, ...Преобразование фигур
Урок 14. Тип урока:. ОНЗ. Тема: «Преобразование фигур». Автор:. С.В. Петрова (МБОУ «СОШ №2 п.г.т. Актюбинский» муниципального Азнакаевского района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию