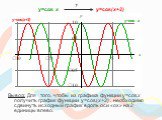
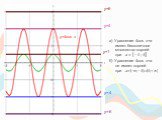
Презентация "Преобразования графиков функций" по математике – проект, доклад
Презентацию на тему "Преобразования графиков функций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 35 слайд(ов).
Слайды презентации
Список похожих презентаций
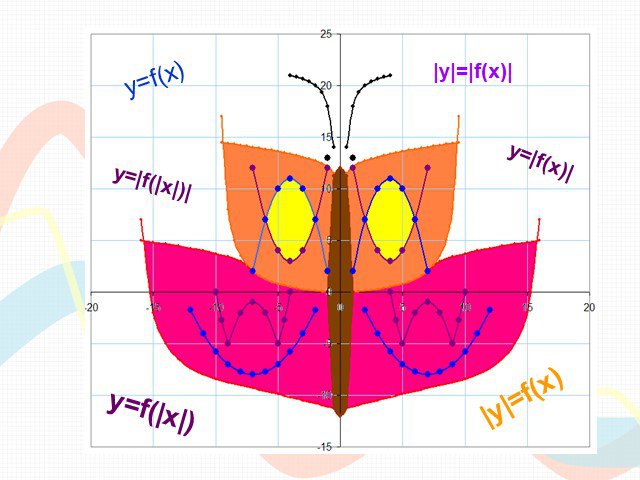
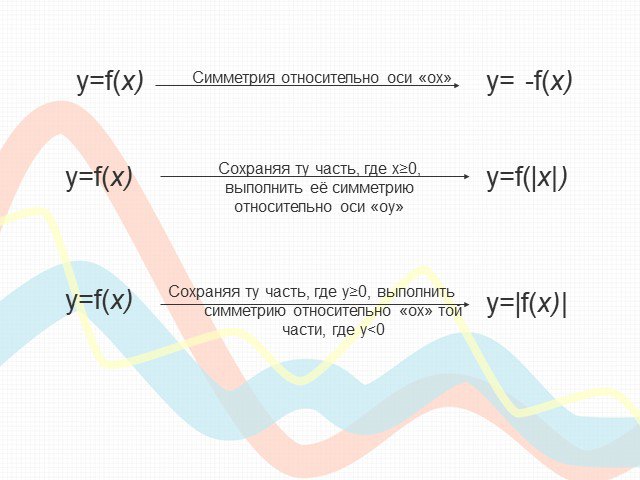
Преобразования графиков функций
A B C x y 0 1. В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2). ...«Примеры преобразования графиков функций»
у = х3 у = -х3 у = (х - 1)3 у = х3 + 1 у = 2х3 у = (2х)3 х = у3. у = х4 у = -х4 у = (-х)4 у = (х-1)4 у = х4-1 у = -2х4 x = y4. у = 3х у = 3-х у = ...Простейшие преобразования графиков функций
Зная вид графика некоторой функции, можно при помощи геометрических преобразований построить график более сложной функции. Рассмотрим график функции ...Построение диаграмм и графиков функций
Диаграмма (график) — это наглядное графическое представление числовых данных. Основные типы диаграмм. Линейчатая Круговая Линии (график). показывает ..."Взаимное расположение графиков функций"
угловой коэффициент прямой, условие параллельности прямых. ТЕМА УРОКА:. Давайте узнаем имя одного математика, который ввел обозначение функций. Для ...Взаимное расположение графиков линейных функций.
Экспресс – опрос:. Какую функцию называют линейной? Что является графиком линейной функции? Какой формулой задаётся прямая пропорциональность? От ...Взаимное расположение графиков линейных функций.
Цели урока. Цели: Рассмотреть разные случаи взаимного расположения графиков линейных функций. Научились распознавать взаимное расположение графиков ...Взаимное расположение графиков линейных функций.
Цели урока:. Выяснить зависимость расположения графиков линейных функций от значений k и b. Научиться по внешнему виду определять взаимное расположение ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Взаимное расположение графиков линейных функций".
"Числа не Боги, они не управляют миром, они показывают, как управляется мир". (поэт, гений немецкой литературы, Гёте). -2 2 5 1 -4 0. 3 6. 4 -1. -3. ...Построение графиков функций, содержащих модуль
Цели урока:. Продолжить формирование навыка построения графиков функций, содержащих модуль; обратить внимание на геометрический смысл модуля; Научить ...Построение графиков функций, содержащих переменную под знаком модуля
1. Построение графиков функций вида y=|f(x)|. По определению модуля, выражение y=|f(x)| равносильно системе f(x), если f(х)0, Y= -f(x), если f(x). ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Свойства производной. Построение графиков функций
Построение графика функции, заданной формулой, начинают с её исследования 1) Находят область определения функции 2) Выясняют, является ли функция ...Решение задач на построение графиков алгебраических функций
Анализ содержания материала. Кто не знает в какую гавань он плывет, для того нет попутного ветра. Сенека. Главной целью данной темы является: научить ...Построение графиков функций, содержащих выражения под знаком модуля
Цель работы:.построение графиков графики функций, содержащие выражения под знаком модуля. Частный случай (под знаком модуля одно выражение и нет ...
Построение графиков функций, содержащих знак модуля
Содержание. I. Введение. II. Основная часть. 1) Понятия и определения. 2) Теоремы, следствия. 3) Построение графиков. III. Заключение. IV. Список ...Построение графиков функций и уравнений, содержащих переменную под знаком модуля
Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля». Тип урока:. «Урок обобщения и систематизации знаний». ...Конспекты
Взаимное расположение графиков линейных функций
Тема:. Взаимное расположение графиков линейных функций. Тип урока. : Совершенствование знаний, умений, и навыков. Цели урока:. Выяснить ...Взаимное расположение графиков линейных функций
Муниципальное образовательное учреждение средняя общеобразовательная школа № 33 с углубленным изучением отдельных предметов. Дзержинского района ...Взаимное расположение графиков линейных функций
Тема урока: « Взаимное расположение графиков линейных функций». Цель урока:. закрепить умения и навыки нахождения углового коэффициента, познакомить ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Взаимное расположение графиков линейных функций
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №10. Урок алгебры для 7 класса. «Взаимное расположение ...Взаимное расположение графиков линейных функций
Учитель: Короленко Евгения Николаевна. Конспект урока по алгебре 7 класса. Тема «Взаимное расположение графиков линейных функций». Цели:. Образовательные:. ...Взаимное расположение графиков линейных функций
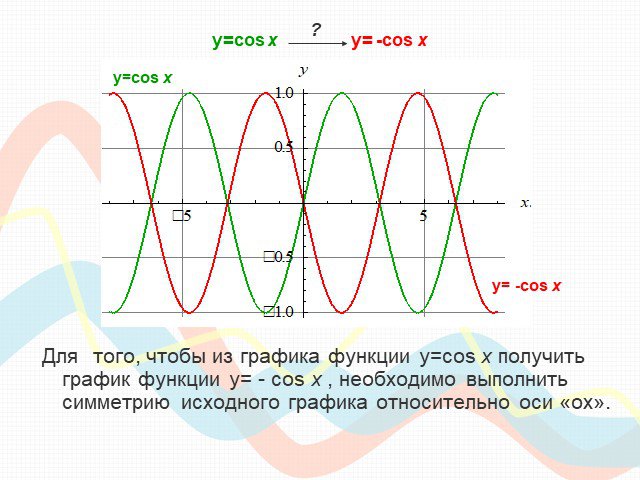
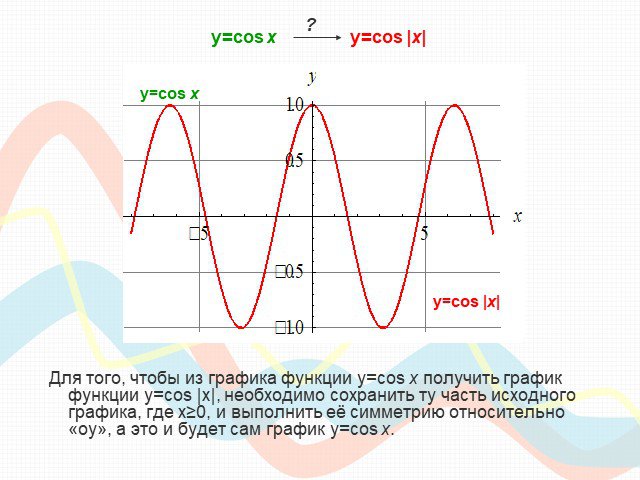
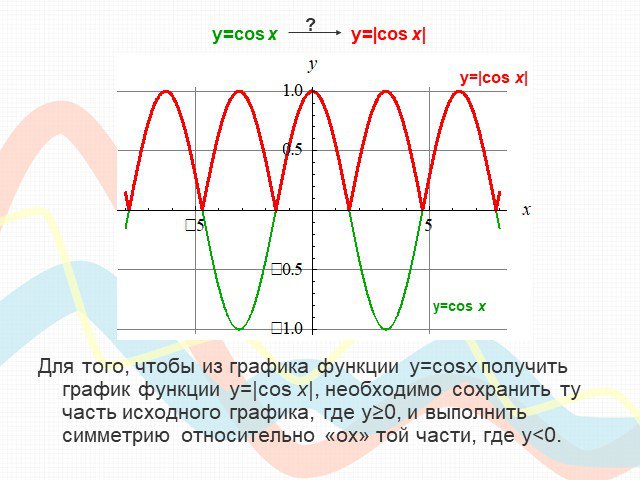
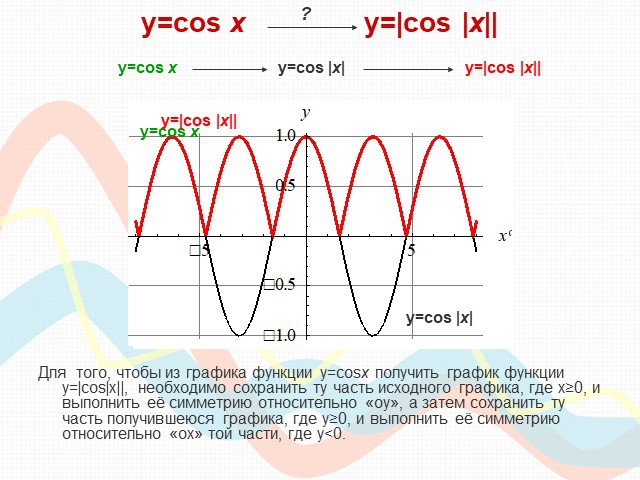
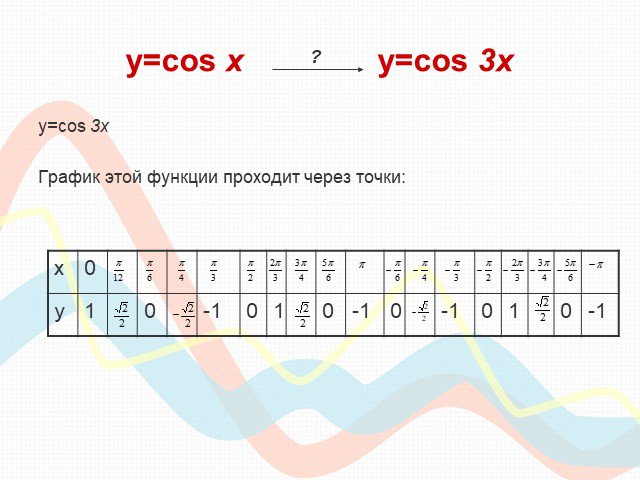
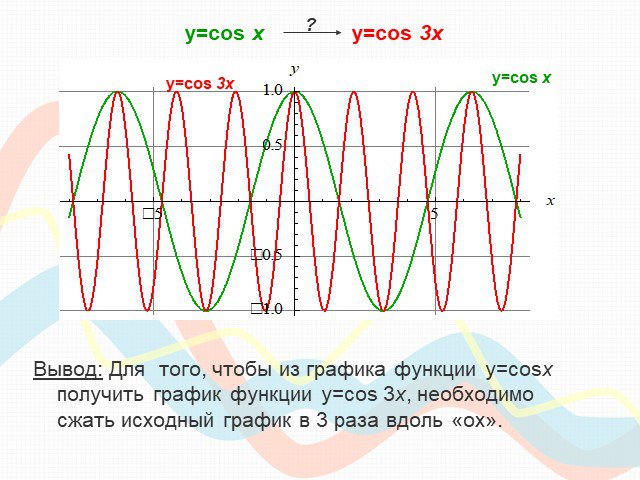
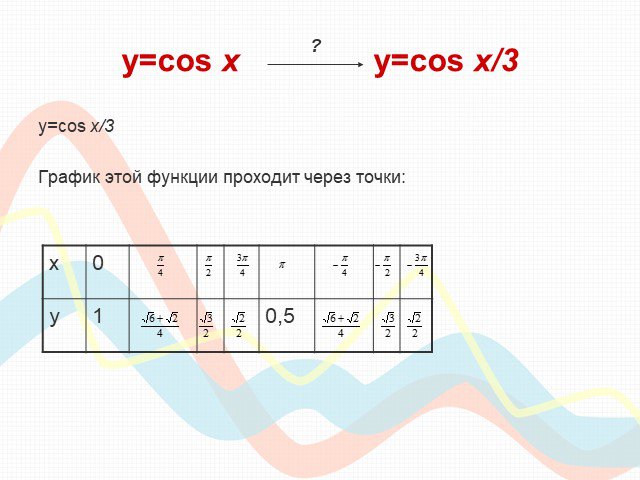
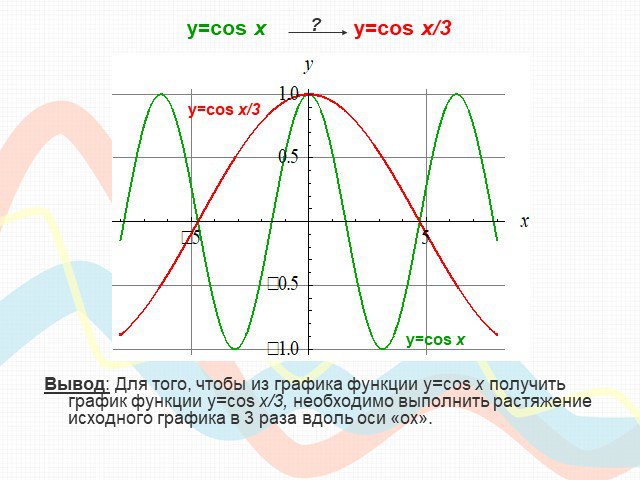
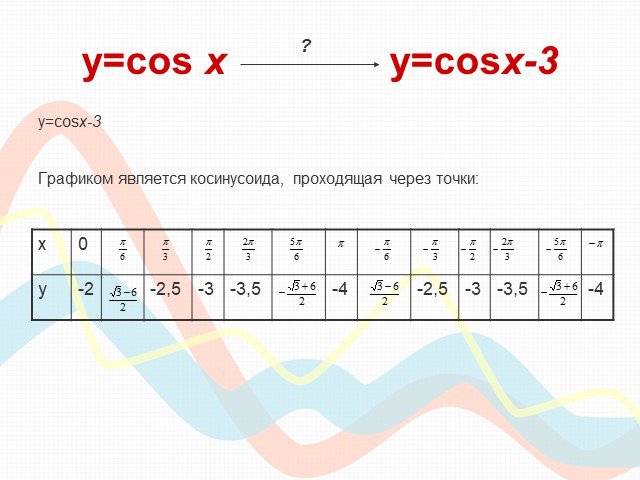
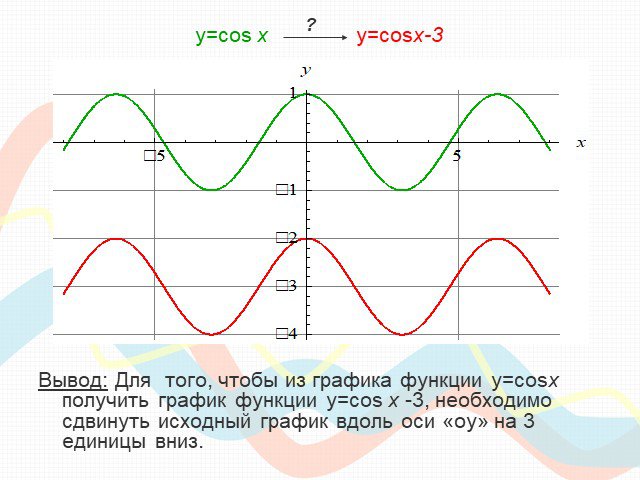
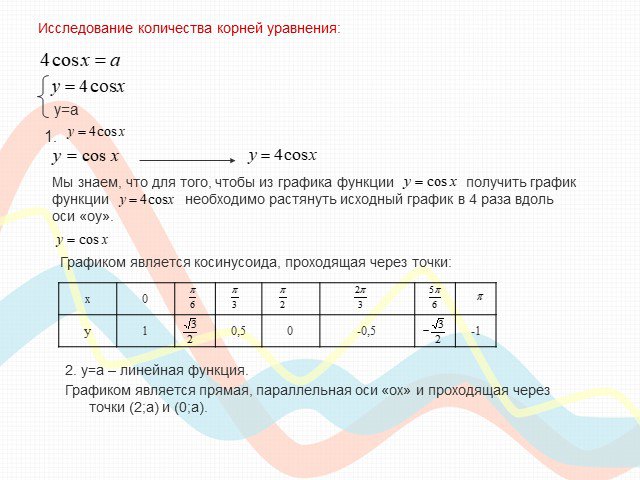
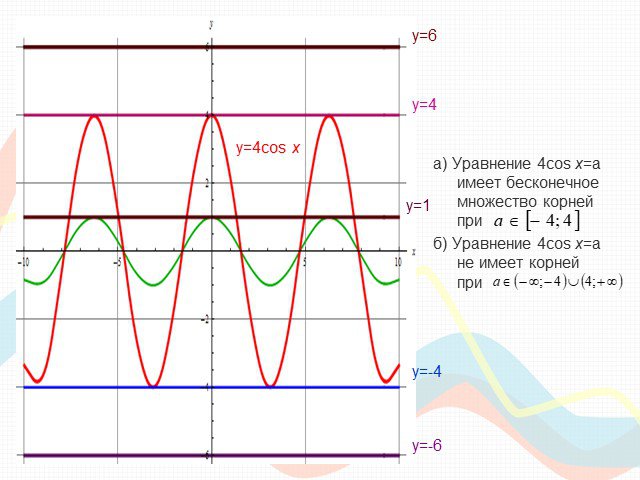
ПЛАН-КОНСПЕКТ УРОКА Конспект урока по теме: «Взаимное расположение графиков линейных функций». . ФИО (полностью). . Чичерова Татьяна ...Преобразование графиков тригонометрических функций
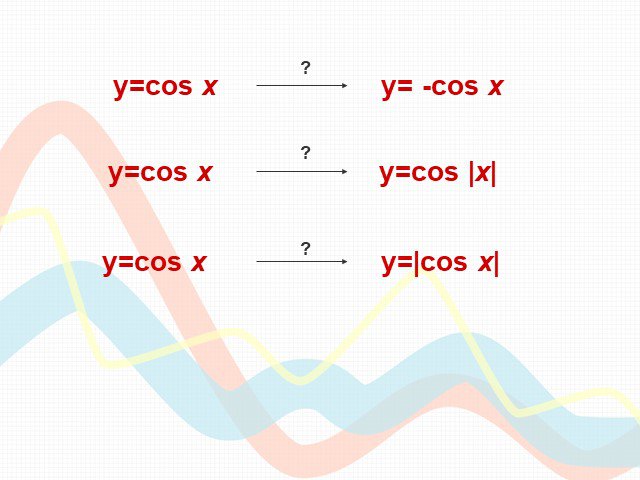
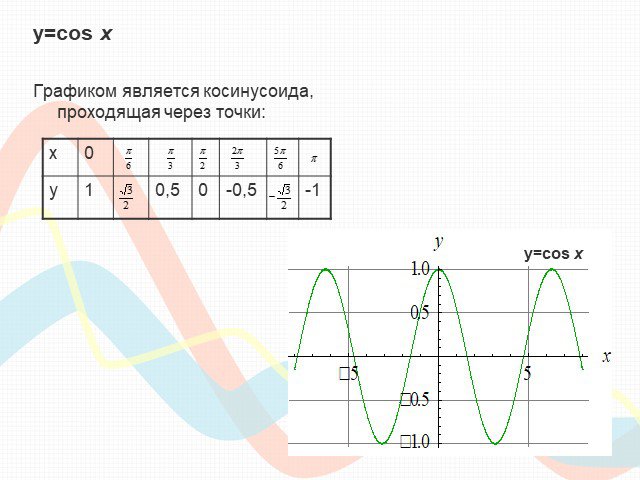
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Преобразование графиков тригонометрических функций
. . Воробьева Ирина Юрьевна. учитель математики. 1 категории. ГУ «Экономический лицей». г. Семей. Методическая разработка урока. ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:35 слайд(ов)
Поделись с друзьями:
Скачать презентацию