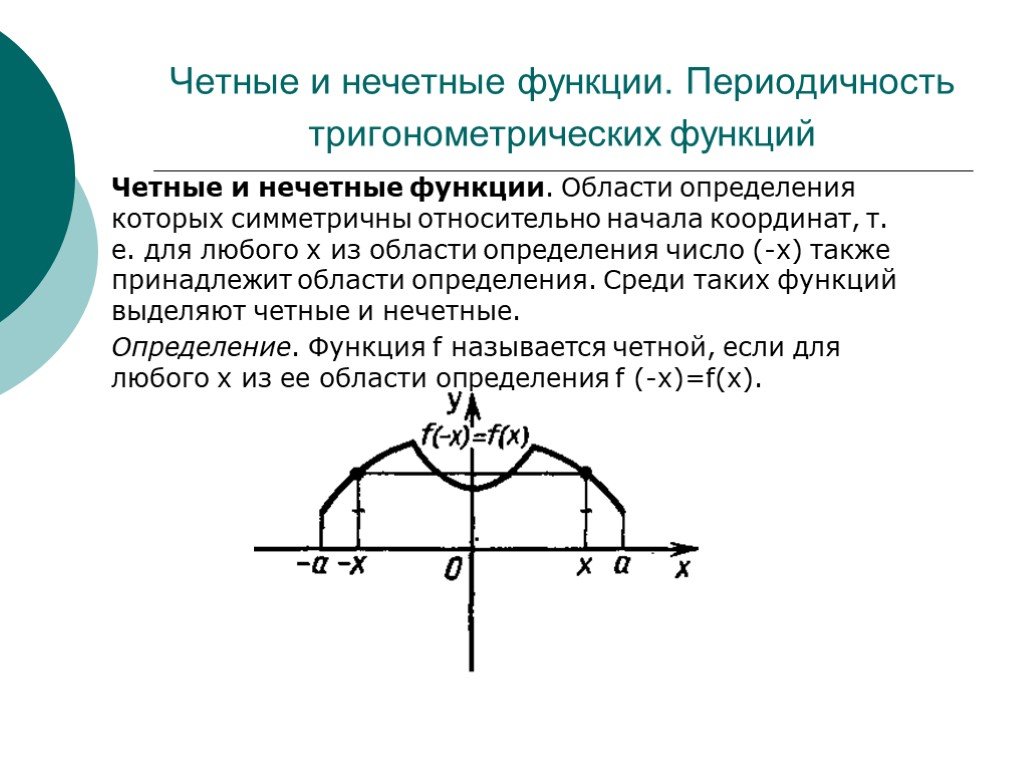
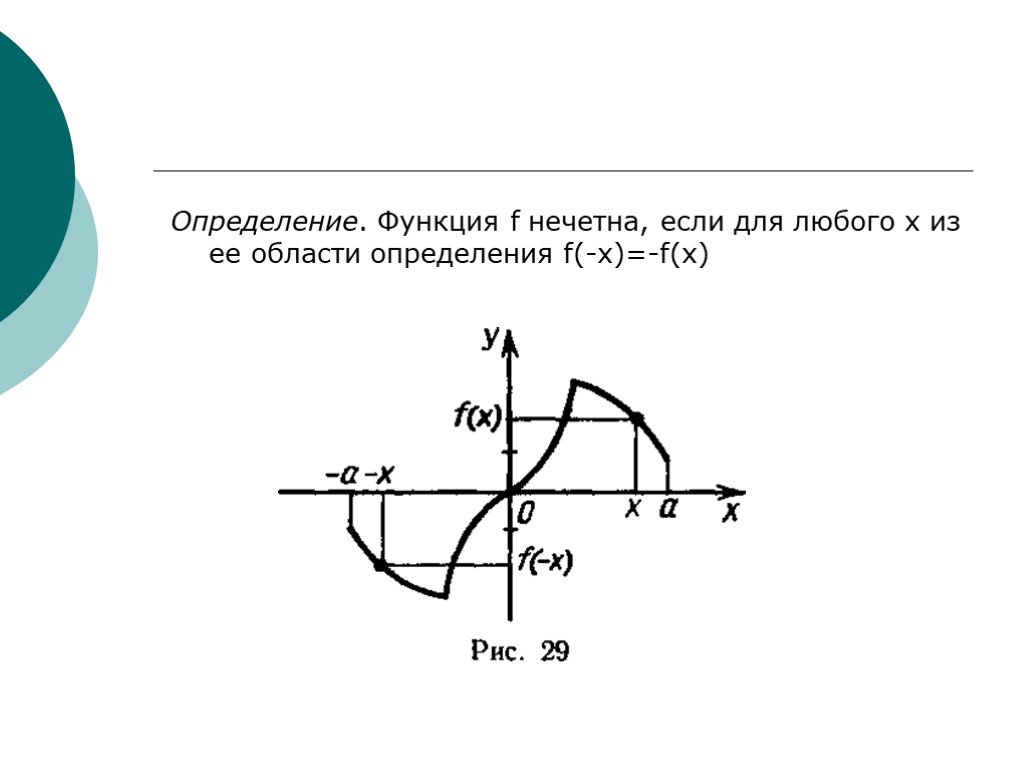
Презентация "Основные свойства функций" по математике – проект, доклад

ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х. Функции обычно обозначают латинскими (а иногда греческими) буквами. Рассмотрим произвольную функцию f. Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f (х). Область определения функции f обозна­чают D (f). Множество, состоящее из всех чисел f (х), таких, что х принадлежит области определения функции f, называют областью значений функции f и обозначают E(f).

Функции и их графики

Объединением множеств А и В называется множество, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В. Функции вида f(x)=p(x), где р(х) — многочлен, называют целыми рациональными функциями, а функции вида где р и q — многочлены, называют дробно-рациональными функциями. Частное определено, если q (х) не обращается в нуль. Поэтому область определения дробно-рациональной функции множество всех действительных чисел, из которого m-iwnvj4cnDi корни многочлена q (х).

Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y = f(x), а х «про­бегает» всю область определения функции f. Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу. Часто функцию задают графически. При этом для любого хо из области определения легко найти соответствующее значение yo =f(xo ) функции.

Четные и нечетные функции. Периодичность тригонометрических функций

Четные и нечетные функции. Области определения которых симметричны относительно начала координат, т. е. для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные. Определение. Функция f называется четной, если для любого х из ее области определения f (-x)=f(x).

Определение. Функция f нечетна, если для любого х из ее области определения f(-x)=-f(x)

Используемые свойства при построении графиков четных и нечетных функций.

1. График четной функции симметричен относительно оси ординат. 2. График нечетной функции симметричен относительно начала координат. Из этих двух правил вытекает следующее: при построении графика четной или нечетной функции достаточно построить его часть для неотрицательных х, а затем отразить полученный график относительно оси ординат (в случае четной функции) или начала координат (в случае нечетной).