Презентация "Основные свойства логарифмов" по математике – проект, доклад
Презентацию на тему "Основные свойства логарифмов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 65 слайд(ов).
Слайды презентации
Список похожих презентаций
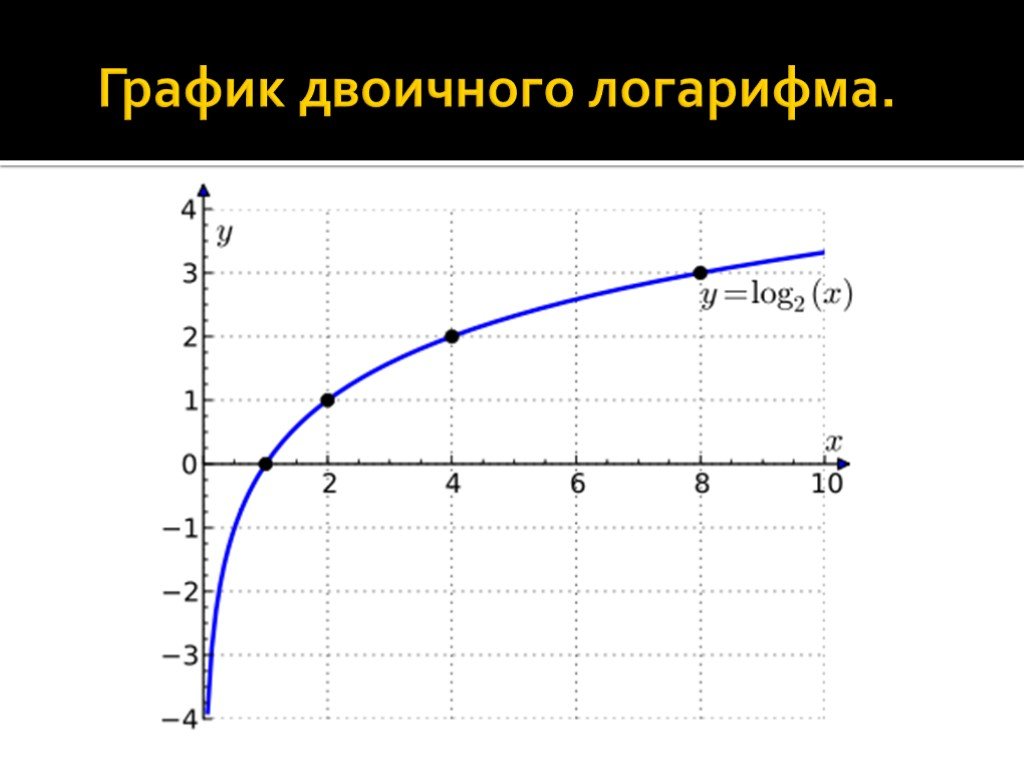
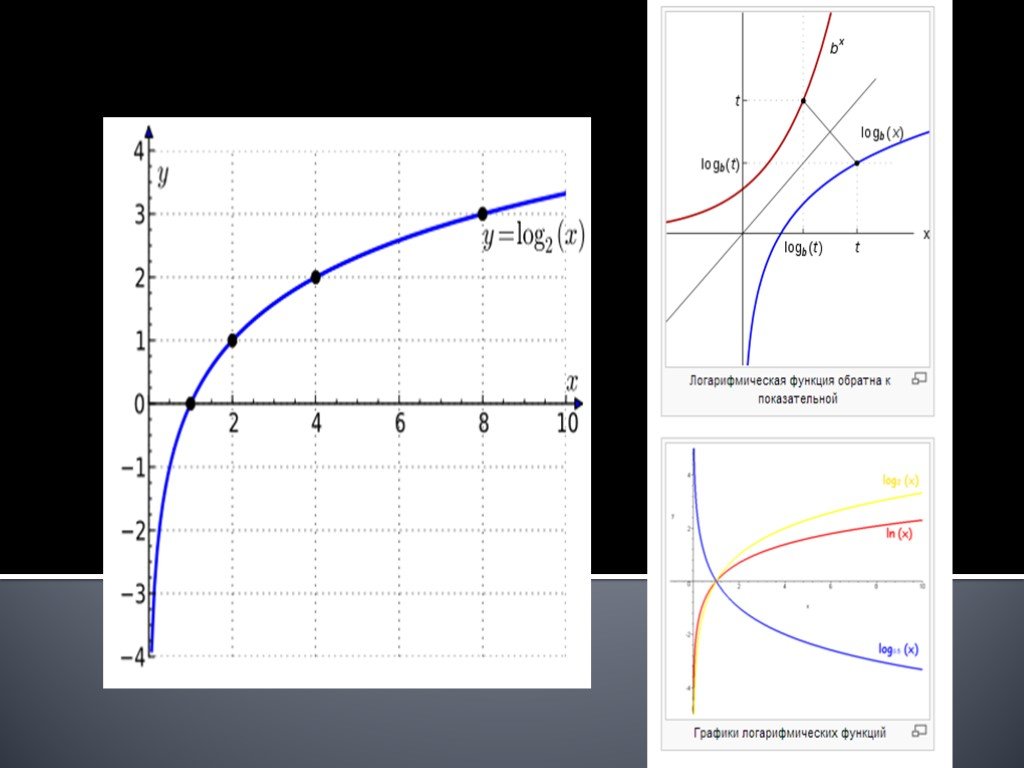
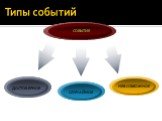
Понятие логарифма, основные свойства логарифмов
Решите уравнение. Мы искали показатель степени, в который надо возвести основание , чтобы получить 27. 1) 0,5х =32, х = - 5. 3) 4х+1+4х = 320 , 4х(4+1) ...Свойства логарифмов
Цель урока:. – обобщить и закрепить определение логарифма числа; – закрепить навыки применения основных свойств логарифма. Основное логарифмическое ...Свойства логарифмов (теория)
Вычислить устно:. . 1. Логарифм произведения равен сумме логарифмов множителей:. 2. Логарифм частного равен логарифмов делимого без логарифма делителя:. ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Свойства логарифмов
Цель. Закрепить понятие логарифма числа Повторить основное логарифмическое тождество, основные свойства логарифмов. 1) 2) 3) 4) 5) 6) 7). . Устно ...Свойства логарифмов
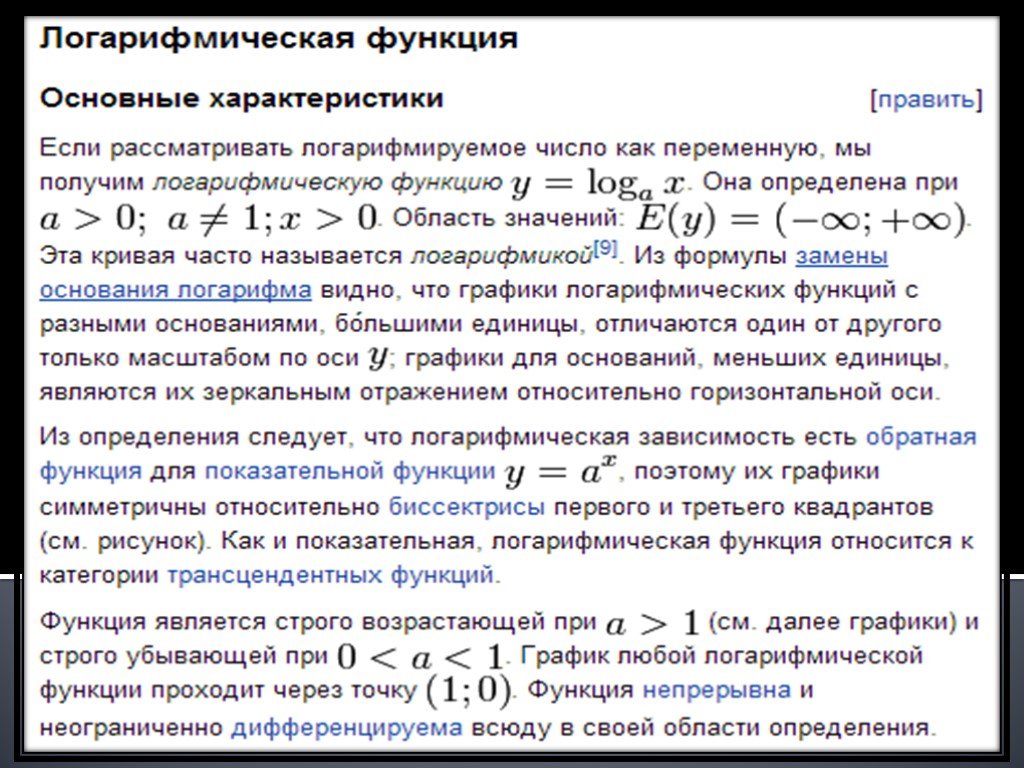
Дайте определение логарифма. a > 0; a ≠ 1; alogab = b b >0. Вычислите :. При каких значениях х существует логарифм. Х > 3 XНе существует ни при каком ...Основные свойства функций
Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому ...Квадратные уравнения. Основные свойства
Из данных уравнений выбрать квадратные. А) х2 – 1 = 0; Б) х3 + 2х – 1 = 0; В) - 1 = 0;. Г) 3х = 0; Д) 2х2 – 5х + 6 = 0; Е) 7х – х2 + 3 = 0. ах2 + ...Основные свойства неопределенного интеграла
Доказательство:. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению. . 3. Неопределенный интеграл от дифференциала некоторой ...Основные формулы тригонометрии
Содержание. Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы суммы и разности ...Основные тригонометрические формулы
Основные формулы тригонометрии и их свойства. Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой ...Основные понятия теории вероятности
Теория вероятностей. Введение. Основные комбинаторные объекты. Элементы теории вероятности. Задачи в которых производится подсчет всех возможных комбинаций ...Прямоугольный треугольник, его свойства
Цели урока:. обучающая – знать свойства прямоугольного треугольника, уметь доказывать их, применять эти свойства при решении задач; развивающая – ...Применение распределительного свойства умножения
Цели урока:. Закрепить навыки применения распределительного свойства умножения для упрощения выражений и устного счета. Проверка выполнения домашнего ...Практическое применение логарифмов в экономике
Непер Джон (1550 - 1617) Известный английский математик, шотландский барон. Математика и астрономия были его увлечениями, а не профессией. Непер вошел ...История возникновения логарифмов
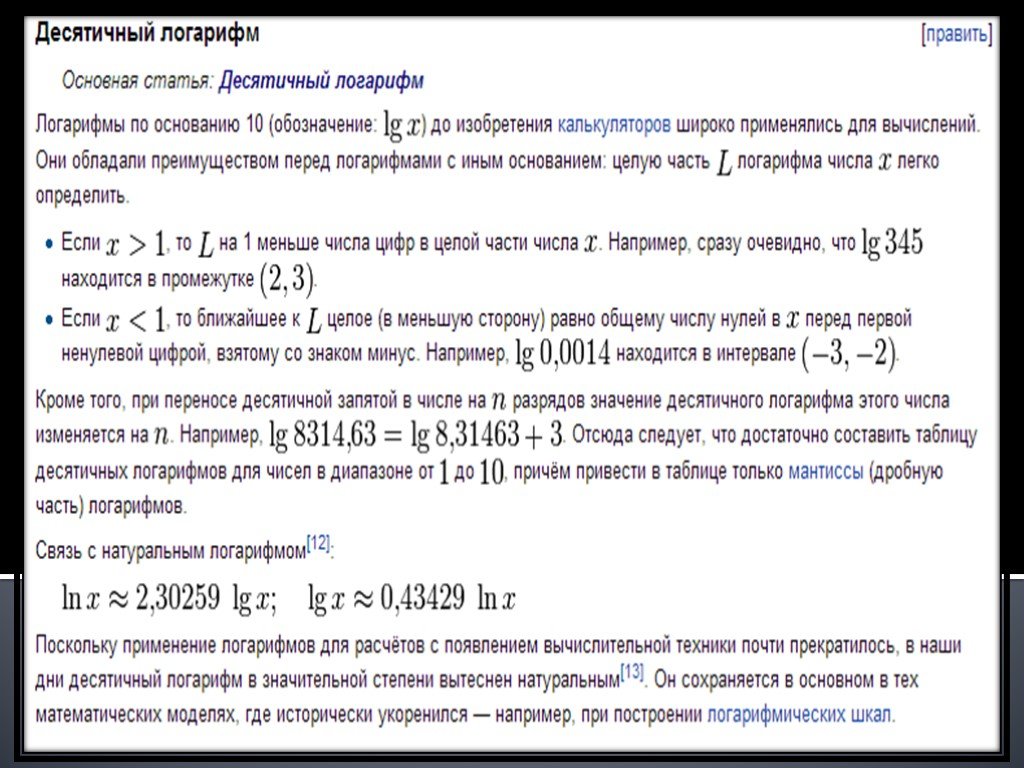
Для чего были придуманы логарифмы? для упрощения вычислений. для ускорения вычислений. для решения астрономических задач. ~. Идея сравнения двух прогрессий: ...Из истории логарифмов
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другим, более древним великим изобретением ...Игра по теме "Степень и ее свойства"
Цели: повторить, обобщить и закрепить знания по данной теме; развивать логическое мышление, смекалку, способность применять теоретический материал ...Дроби и их свойства
Проверка домашнего задания. Iвариант 1.Представьте данную дробь со знаменателем 36 2 9. IIвариант 1.Представьте данную дробь со знаменателем 24 5 ...Действия с натуральными числами и их свойства
"Тропинка к истине сложна, И потому в мышленье чистом Отвага дерзкая нужна Не менее, чем альпинистам» "Мыслители" Евгений Винокуров. I этап. «Разминка». ...Конспекты
Свойства логарифмов
Государственное областное бюджетное. профессиональное образовательное учреждение. «ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ». Методическая ...Формула Шеннона. Свойства логарифмов
Конспект. интегрированного урока алгебры и информатики. по теме «Формула Шеннона. Свойства логарифмов» в 10 классе. Подготовили: Грызайкина Лидия ...Логарифмы. Свойства логарифмов
Шкарупина Наталья Сергеевна. учитель математики. МАОУ «Гимназия № 1 МО «Ахтубинский район» Астраханской области. Урок математики по теме. «Логарифмы. ...Свойства логарифмов
Муниципальное бюджетное общеобразовательное учреждение. . лицей № 35г. Ставрополя. «. Свойства. . логарифмов. ». урок ...Логарифм числа. Свойства логарифмов
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа № 2 р.п Сенной. вольского района саратовской области». . ...Логарифмы. Свойства логарифмов
Филиал боу СПО. «. ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ. ». минздравсоцразвития чувашии Г. КАНАШ чувашской республики. . «. Утверждаю. ». . зав ...Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Справочные сведения. Логарифмом. . положительного числа b. по основанию ...Свойства логарифмов
Урок по алгебре и началам анализа в 11 классе. . Тема: Свойства логарифмов. Цель. :. Организовать работу учащихся по изучению и применению свойств ...Степень с рациональным показателем и ее свойства
Марьевский филиал. МОУ Ивановской средней. общеобразовательной школы. Алгебра 9 класс. . Молчанова. . Валентина Алексеевна. ...Степень и ее свойства
Урок по алгебре "Степень и ее свойства". . Тип урока:. . обобщение и систематизация полученных ранее знаний по теме “Степень и ее свойства”. Форма ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 марта 2019
Категория:Математика
Содержит:65 слайд(ов)
Поделись с друзьями:
Скачать презентацию