Презентация "Основные тригонометрические формулы" по математике – проект, доклад

Скачать презентацию (0.38 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Презентацию на тему "Основные тригонометрические формулы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).

Скачать презентацию (0.38 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Основные тригонометрические формулы

Подготовила ученица 10 класса: Панькина Диана Учитель: Малянов Иван Иванович Сосновская СОШ 2012 г.

Слайд 2

Основные формулы тригонометрии и их свойства

Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой прямоугольный треугольник. Из курса геометрии мы знаем, что у него есть два катета и гипотенуза, причем угол между двумя катетами прямой - то есть равен 90o, или π/2 радиан.

Рассмотрим угол α, который образован одним из катетов и гипотенузой.

Синусом угла α называется отношение длин противолежащего катета к гипотенузе. Косинусом угла α называется отношение длин прилежащего катета к гипотенузе. Тангенсом угла α называется отношение длин противолежащего катета к прилежащему. Котангенсом угла α называется отношение длин прилежащего катета к противолежащему.

Из определений тригонометрических функций сразу же следуют тригонометрические тождества:

Слайд 4

Связь между тригонометрическими функциями одного и того же аргумента

Слайд 5

Тригонометрические функции двойного и половинного аргумента

Слайд 6

Формулы, что выражают тригонометрические функции через тангенс половинного угла

Слайд 7

Тригонометрические функции суммы и разности углов

Слайд 8

Значения синуса, косинуса, тангенса, котангенса

sin(α)=OA cos(α)=OC tg(α)=DE ctg(α)=MK R=OB=1

Слайд 9

Пример решения тригонометрического уравнения при помощи тригонометрической формулы

Пример 1. sin3x = sinx.

Решение. Перенесем sinx в левую часть уравнения и полученную разность преобразуем в произведение. sin3x - sinx == 0; 2sinx · cos2x = 0. Из условия равенства нулю произведения получим два простейших уравнения.

sinx = 0 или cos2x = 0.

x1 = p n, n Î Z, x2 = p /4 + p n/2, n Î Z

Ответ: x1 = p n, n Î Z, x2 = p /4 + p n/2, n Î Z.

Список похожих презентаций

Основные формулы тригонометрии

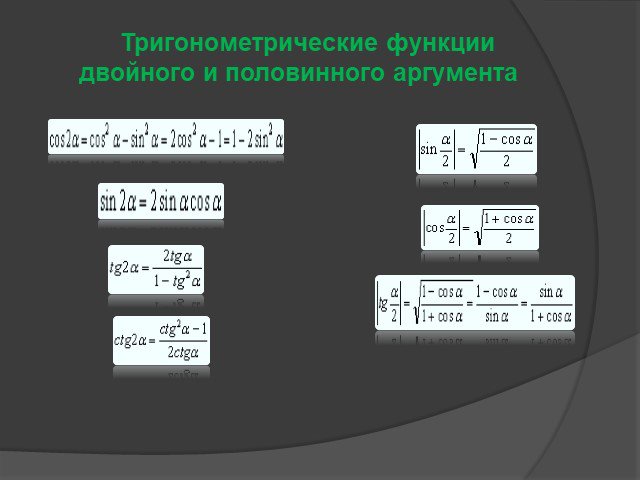
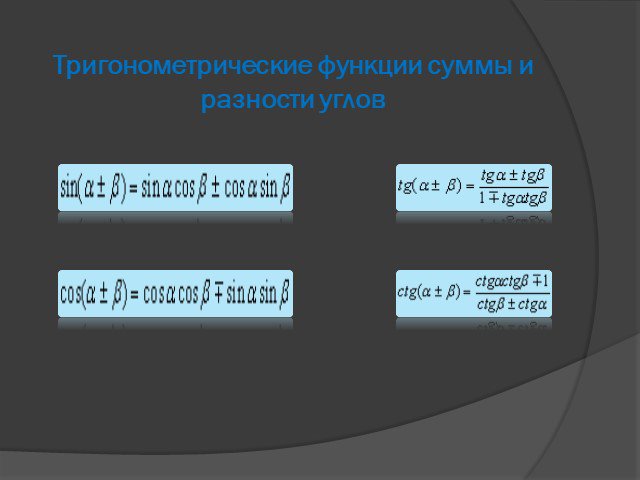
Содержание. Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы суммы и разности ...

Тригонометрические формулы

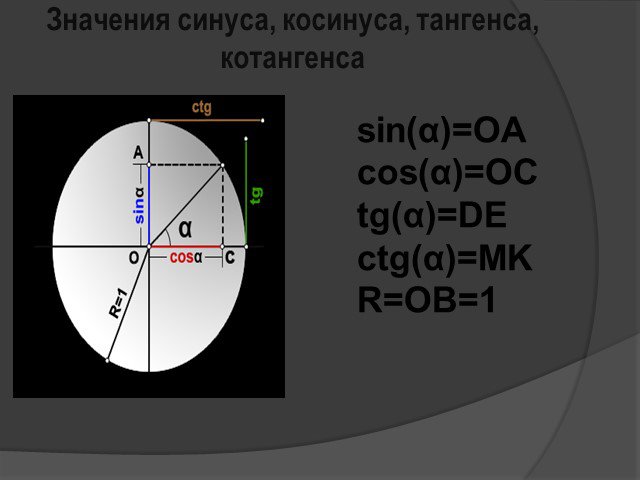
Цель урока. Повторить и систематизировать изученный материал Подготовиться к контрольной работе. Задачи урока. Повторить определение синуса, косинуса, ...

Основные формулы тригонометрии

Могут ли одновременно выполняться равенства? Правильный ответ: Да 17.06.2019. . Нет. Вычислите:. учитель математики Кустова М.О. . - 0,6. . . . . ...

Тригонометрические формулы

Математический турнир. Тур I. В какой четверти лежит угол α, если выполняется условие Sinα>0, cosα. Определите знак значения функции cos150˚ ( « - ...

Основные тригонометрические функции

Пояснительная записка. В результате изучения курса математики учащиеся должны понимать, что функция – математическая модель, позволяющая описывать ...

Тригонометрические формулы

Рассмотрим следующие вопросы:. радианная мера угла; поворот точки вокруг начала координат; определение синуса, косинуса и тангенса произвольного угла; ...

Основные аксиомы стереометрии

Скажи мне – и я забуду. Покажи мне – и я запомню. Вовлеки меня – и я научусь. Древняя китайская пословица. Четыре равносторонних треугольника. Геометрия ...

Основные фигуры

А В С Е. Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,…. Планеты и звезды в масштабе вселенной. Птицы и самолеты в небе. Атомы ...

Основные теоремы теории вероятностей

Литература и интернет - ресурсы. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учебное пособие. М.: Академия, 2003. – 448 ...

Основные свойства неопределенного интеграла

Доказательство:. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению. . 3. Неопределенный интеграл от дифференциала некоторой ...

Граф и его элементы. Основные определения

Переход по слайдам осуществляется только по нажатию левой кнопки мыши клик мыши!!! Если есть мигающая стрелка, значит нужно нажатие левой кнопки мыши ...

Интерполяционные формулы

Пусть точка х лежит в окрестности середины интервала содержащего 2n+1 равноотстоящих с шагом h узла интерполирования. Для интерполирования функции ...

Решение задач с использованием формулы полной вероятности и формулы Бейеса

Формула полной вероятности. Формула Бейеса P(Hi|A) = =. Задачи. 1. В сборочный цех поступили детали с трех станков. На первом станке изготовлено 51% ...

Однородные тригонометрические уравнения

Кроссорд. 1. Значение переменной, обращающее уравнение в верное равенство 2. Единица измерения углов 3. Числовой множитель в произведении 4. Раздел ...

Определение запыленности воздуха по листьям деревьев с использованием формулы Пика

Введение. В последние годы, наряду с изменениями климата, происходит значительное увеличение антропогенной нагрузки на природные и урбанизированные ...

Обратные тригонометрические функции

Содержание: Обратные тригонометрические функции, свойства, графики Историческая справка Преобразование выражений, содержащих обратные тригонометрические ...

Обратные тригонометрические функции

Историческая справка. Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике ...

Обратные тригонометрические функции

15.05.2019. I. Математический диктант. 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная. I вариант y=sin x II вариант ...

Логарифм. Основные понятия

. . . . Десятичные логарифмы. Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная ...

Квадратные уравнения. Основные свойства

Из данных уравнений выбрать квадратные. А) х2 – 1 = 0; Б) х3 + 2х – 1 = 0; В) - 1 = 0;. Г) 3х = 0; Д) 2х2 – 5х + 6 = 0; Е) 7х – х2 + 3 = 0. ах2 + ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.