Конспект урока «Тригонометрические формулы» по математике
Тема: Тригонометрические формулы (25 часов)
Урок 6 – 7: Зависимость между синусом, косинусом и тангенсом одного и того же угла.
Цель: изучить зависимость между синусом, косинусом и тангенсом одного и того же угла.
Для достижения поставленной цели необходимо:
-
Знать:
-
формулировки определений основных тригонометрических функций (синуса, косинуса и тангенса);
-
знаки тригонометрических функций по четвертям;
-
множество значений тригонометрических функций;
-
основные формулы тригонометрии.
-
Понимать:
-
что пользоваться основным тригонометрическим тождеством можно только для одного и того же аргумента;
-
алгоритм вычисления одной тригонометрической функции через другую.
-
Применить:
-
умение правильно выбрать нужную формулу для решения конкретного задания;
-
умение работать с простыми дробями;
-
умение выполнять преобразование тригонометрических выражений.
-
Анализ:
-
анализировать ошибки в логике рассуждения.
-
Синтез:
-
предложить свой способ решения примеров;
-
составить кроссворд, используя полученные знания.
-
Оценка:
-
знаний и умений по данной теме для использования в других разделах алгебры.
Оборудование: макет тригонометрической окружности, раздаточный справочный материал с формулами и таблицами значений тригонометрических функций, компьютер, мультимедийный проектор, презентация, листы с заданиями для самостоятельной работы.
Ход урока:
-
Организационный момент.
Приветствие. Сообщение цели урока и плана работы на уроке.
-
Актуализация знаний и умений.
Учащимся раздаются карты урока и даются пояснения как с ними работать.
На экран выводятся вопросы; учащиеся записывают ответы в тетрадь; преподаватель выводит на экран правильный ответ. После окончания опроса учащиеся выставляют баллы в карту урока для Задания № 1.
-
В какой четверти находится угол в 1 радиан и чему он примерно равен?
(В I четверти, 1 рад.57,30).
-
Какое слово пропущено в определение функции синус?
Синусом угла называется ............ точки единичной окружности. (Ордината)
-
Какое слово пропущено в определении функции косинус?
Косинусом угла называется............ точки единичной окружности (Абсцисса).
-
Допишите формулу:

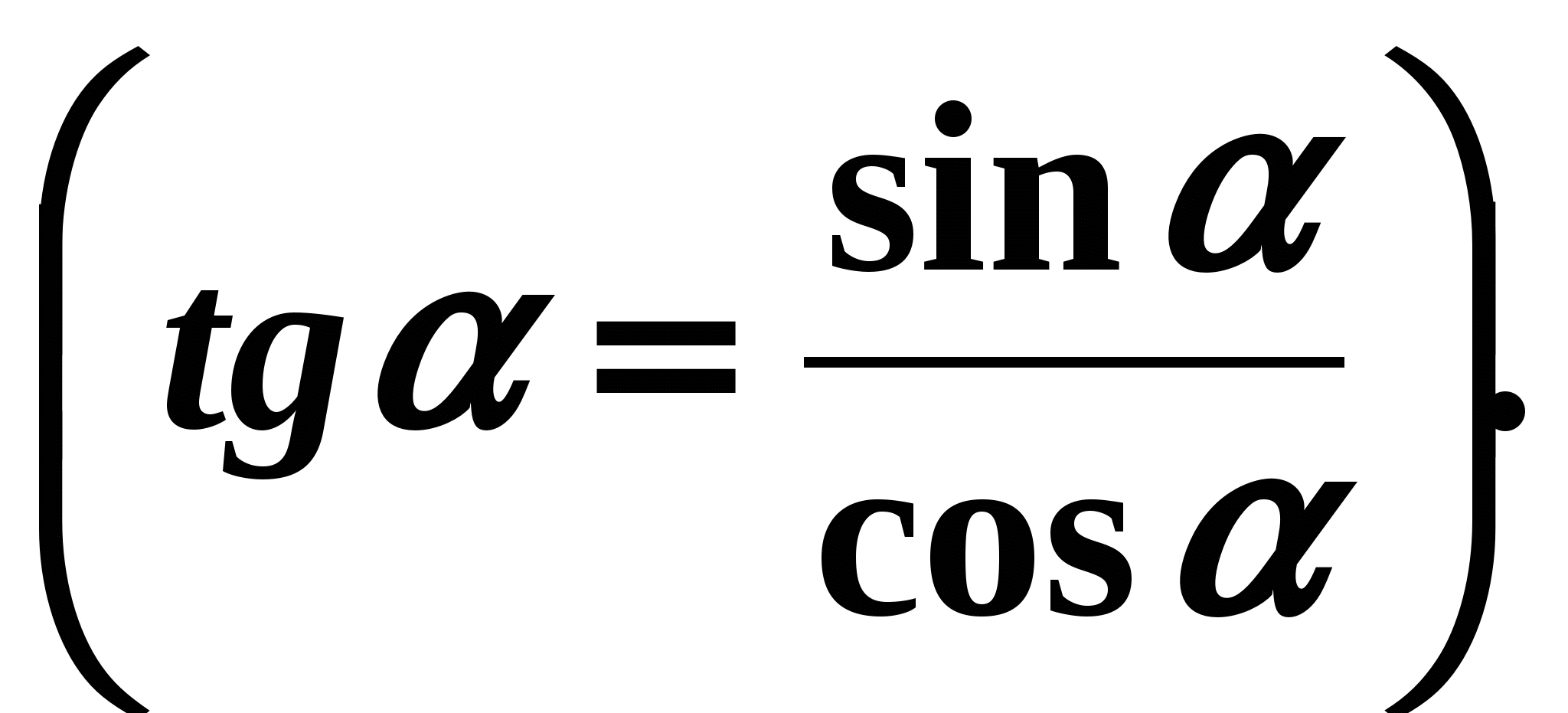
-
Определите знак произведения:
 (
(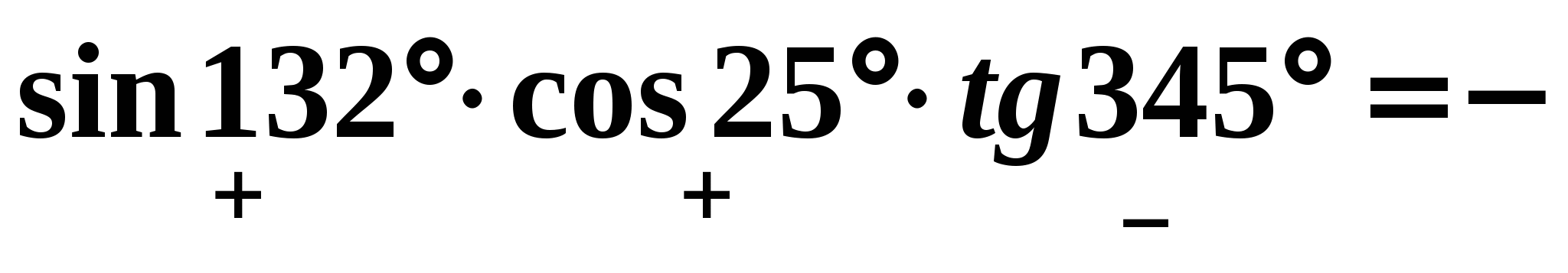 )
)
-
Какие значения может принимать синус?
![]()
-
Вычислите:
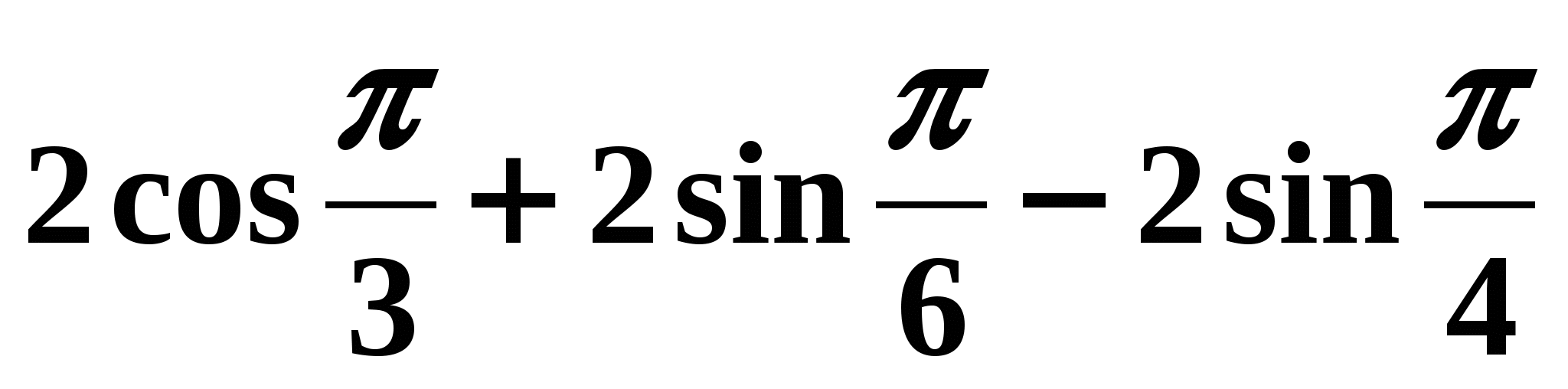
( ![]() )
)
-
Объяснение нового материала.
И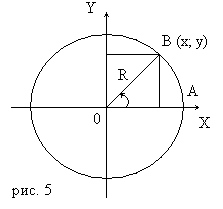 зобразим единичную окружность с центром в точке О. Пусть при повороте радиуса ОА, равного R, на угол получен радиус ОВ (рис. 5). Тогда по определению
зобразим единичную окружность с центром в точке О. Пусть при повороте радиуса ОА, равного R, на угол получен радиус ОВ (рис. 5). Тогда по определению ![]() где
где ![]() – абсцисса точки В,
– абсцисса точки В, ![]()
![]() – ее ордината.
– ее ордината.
Отсюда следует, что ![]()
Точка В принадлежит окружности. Поэтому ее координаты удовлетворяют уравнению ![]()
![]()
Воспользовавшись тем, что ![]() получим
получим
![]()
![]() (1). Мы получили равенство справедливое при любых значениях входящих в него букв. Как называются такие равенства? Правильно – тождества. Равенство (1) называется основным тригонометрическим тождеством.
(1). Мы получили равенство справедливое при любых значениях входящих в него букв. Как называются такие равенства? Правильно – тождества. Равенство (1) называется основным тригонометрическим тождеством.
В равенстве (1) может принимать любые значения. Самостоятельно завершите запись:
|
|
| |
| 2. |
|
|
| 3. |
|
|
| 4. |
|
|
Проверьте правильность вашей записи. Выставите себе баллы в карту урока для Задания № 2.
Продолжаем. Мы вывели основное тригонометрическое тождество, а для чего оно нам нужно?
Правильно – для нахождения по одному известному нам значению синуса значение косинуса и наоборот. Вот теперь мы с вами всегда сможем пользоваться основным тригонометрическим тождеством, но главное – для одного и того же аргумента.
Учащимся в тетради предлагается самостоятельно выразить из основного тригонометрического тождества синус через косинус и косинус через синус.
Для проверки к доске вызываются два ученика. Одному предлагается выразить синус через косинус, второму – косинус через синус.
На экран выводится верный ответ: ![]()
Учащиеся проверяют свои ответы и выставляют баллы в карту урока для Задания № 3.
В этих формулах от чего зависит знак перед корнем? (От того, в какой четверти расположен угол тригонометрической функции, которую мы определяем).
Пример 1. Вычислить ![]() если
если ![]()
Определим четверть, в которой находится угол ![]() . Четверть – III.
. Четверть – III.
Вспомним, что синус в третьей четверти отрицательный, т. е. в формуле (2) перед корнем нужно поставить знак « – »:
![]()
Пример 2. Вычислить ![]() если
если ![]()
Определяем четверть, в которой находится угол . Четверть – IV, косинус в четвертой четверти положителен. Поэтому в формуле (3) перед корнем нужен знак « + »:
![]()
Выясним теперь зависимость между тангенсом и котангенсом. По определению тангенса и котангенса ![]()
Перемножая эти равенства, получаем:
![]()
Из равенства (4) можно выразить ![]() через
через ![]() и наоборот:
и наоборот:
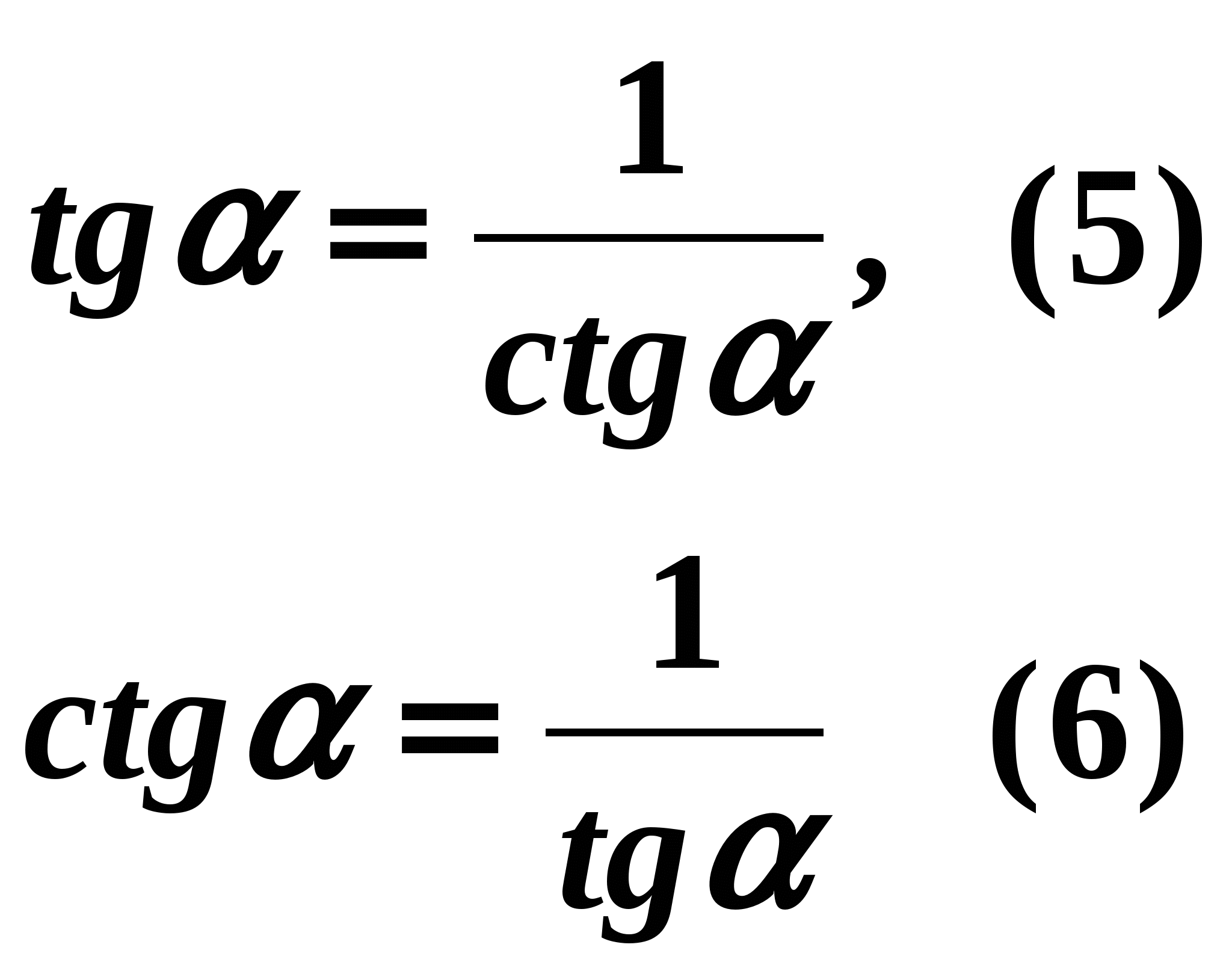
Равенства (4) – (6) верны при всех значениях, при которых ![]() имеют смысл, т. е. при
имеют смысл, т. е. при ![]()
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также котангенсом и синусом одного и того же аргумента.
Разделив обе части равенства (1) на ![]() , получим:
, получим:
![]() т.е.
т.е. ![]()
Если обе части равенства (1) разделить на ![]() , то будем иметь:
, то будем иметь:
![]() т.е.
т.е. ![]()
Рассмотрим примеры использования выведенных формул для нахождения значений тригонометрических функций по известному значению одной из них.
Пример 1. Найдем ![]() если известно, что
если известно, что ![]()
Решение:
-
Найдем сначала
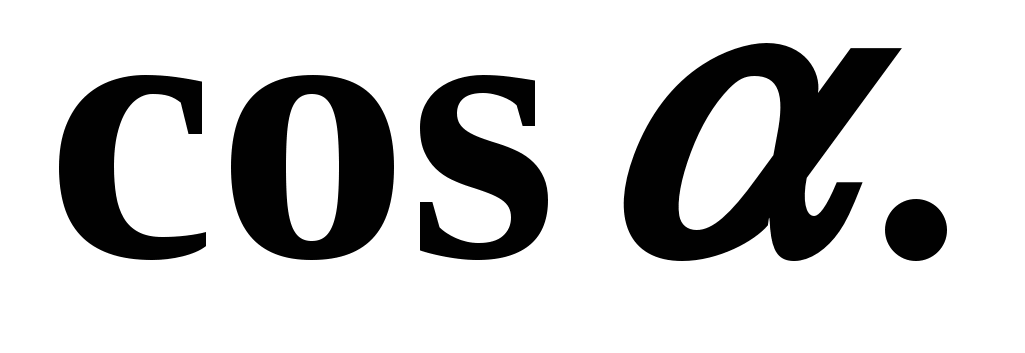 Для этого воспользуемся формулой (3). Так как является углом 2 четверти, то его косинус отрицателен. Значит,
Для этого воспользуемся формулой (3). Так как является углом 2 четверти, то его косинус отрицателен. Значит, 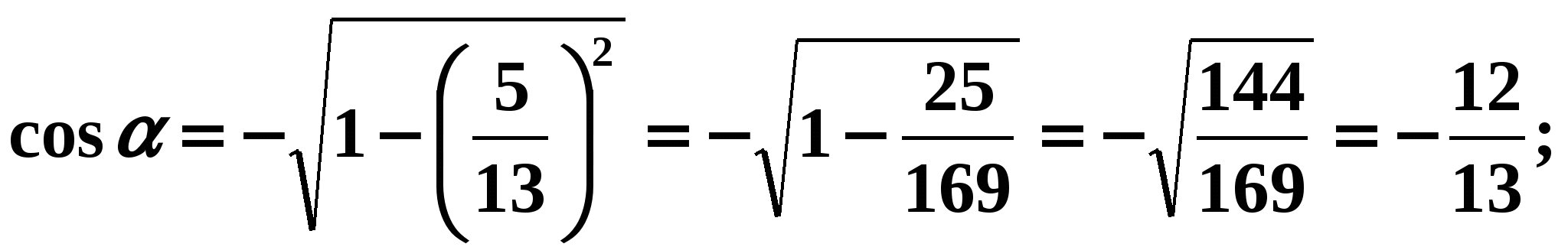
-
Зная синус и косинус можно найти его тангенс:
![]()
-
Для отыскания котангенса угла удобно воспользоваться формулой (6):
![]()
Ответ: ![]()
Пример2. Известно, что ![]() . Найдем все остальные тригонометрические функции.
. Найдем все остальные тригонометрические функции.
Решение:
-
Воспользуемся формулой (7). Имеем:
![]()
![]() ,
, ![]() . По условию задачи угол является углом 1 четверти, поэтому его косинус положителен. Значит
. По условию задачи угол является углом 1 четверти, поэтому его косинус положителен. Значит ![]()
-
Зная
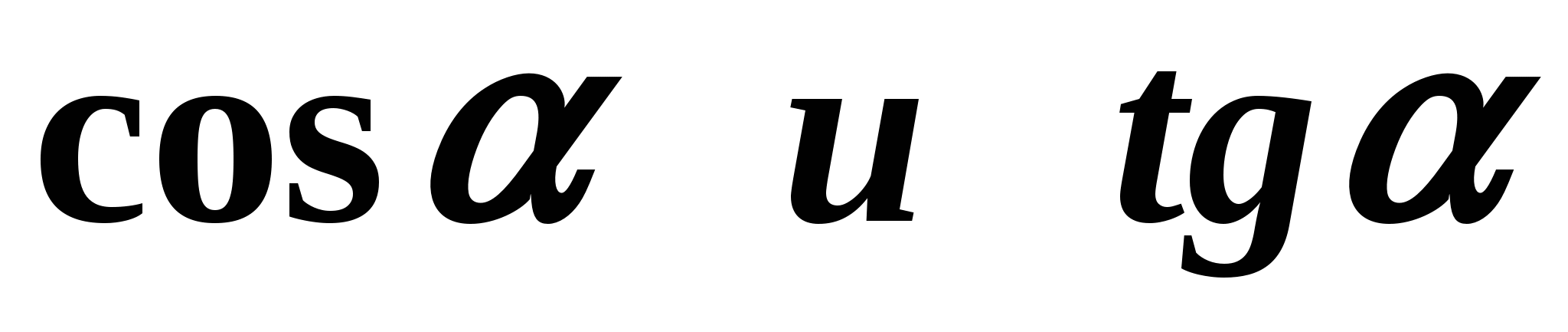 , можно найти
, можно найти 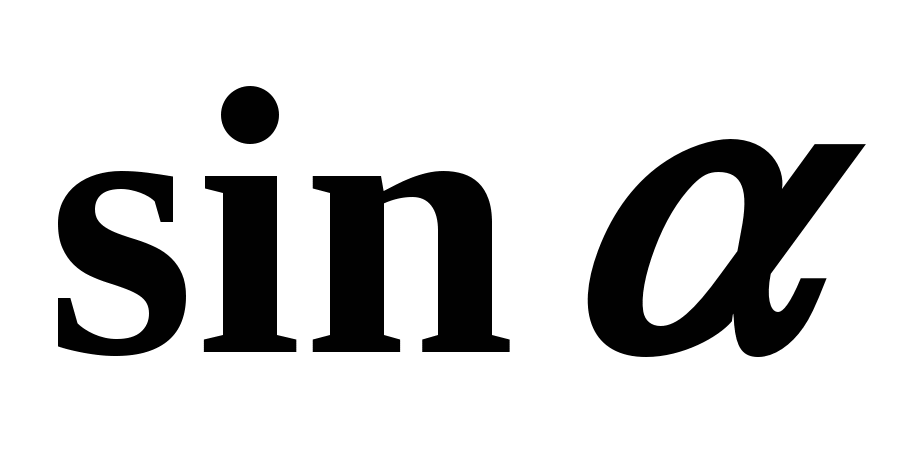 . Из формулы
. Из формулы 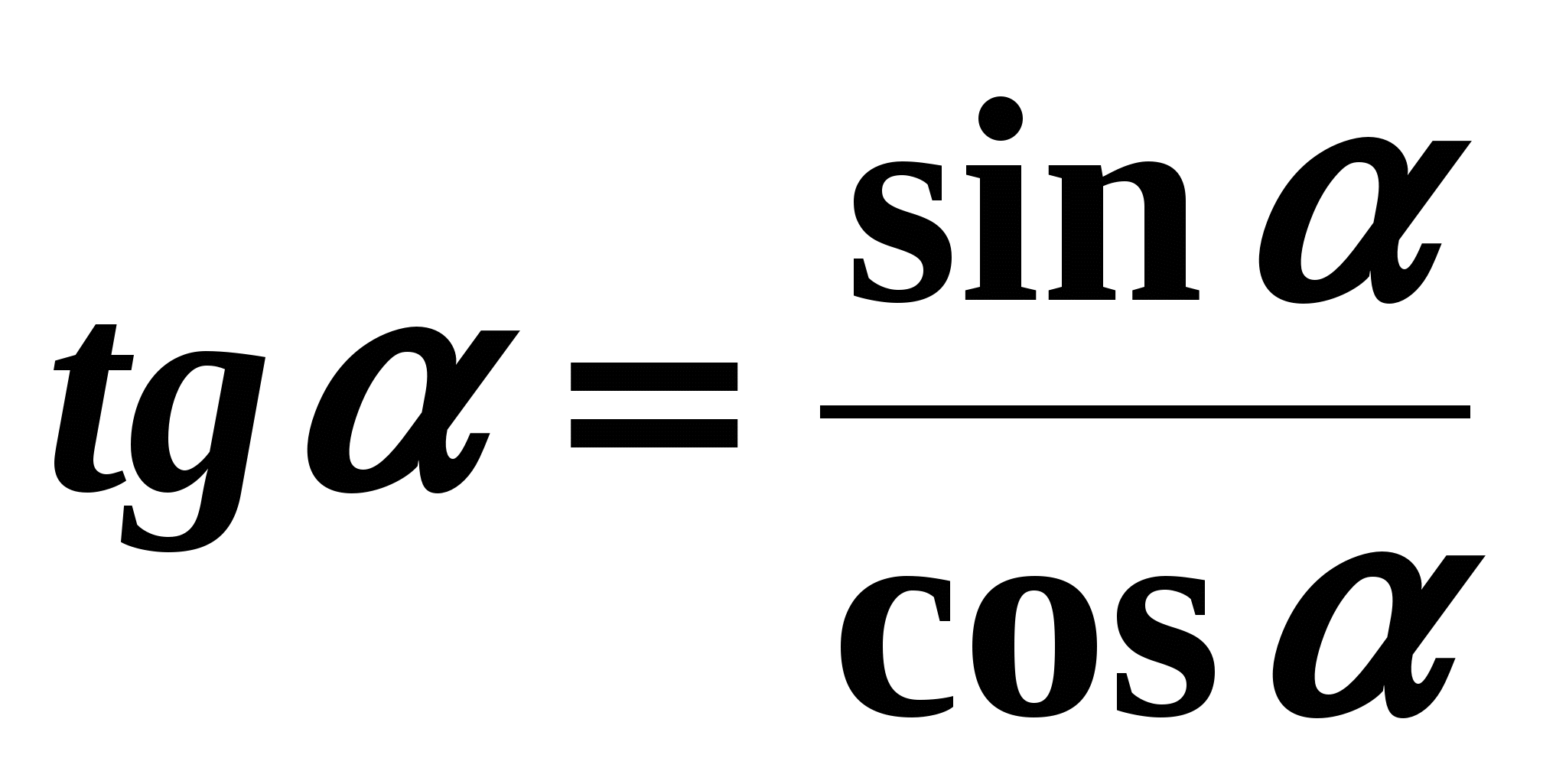 получим:
получим:
![]()
-
По известному
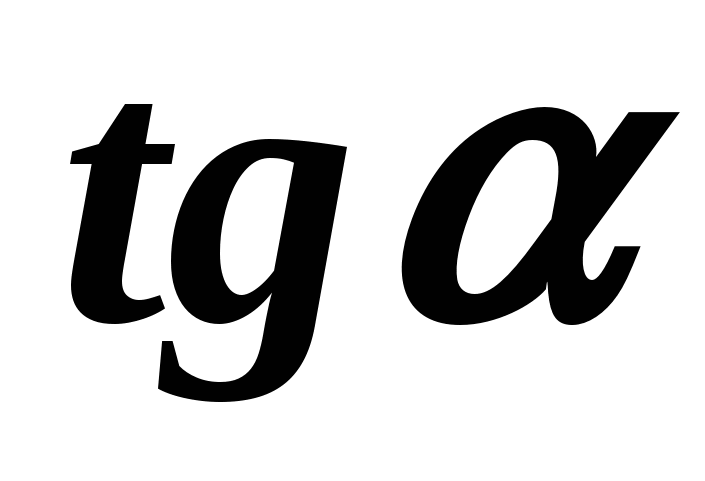 легко найти
легко найти  :
: 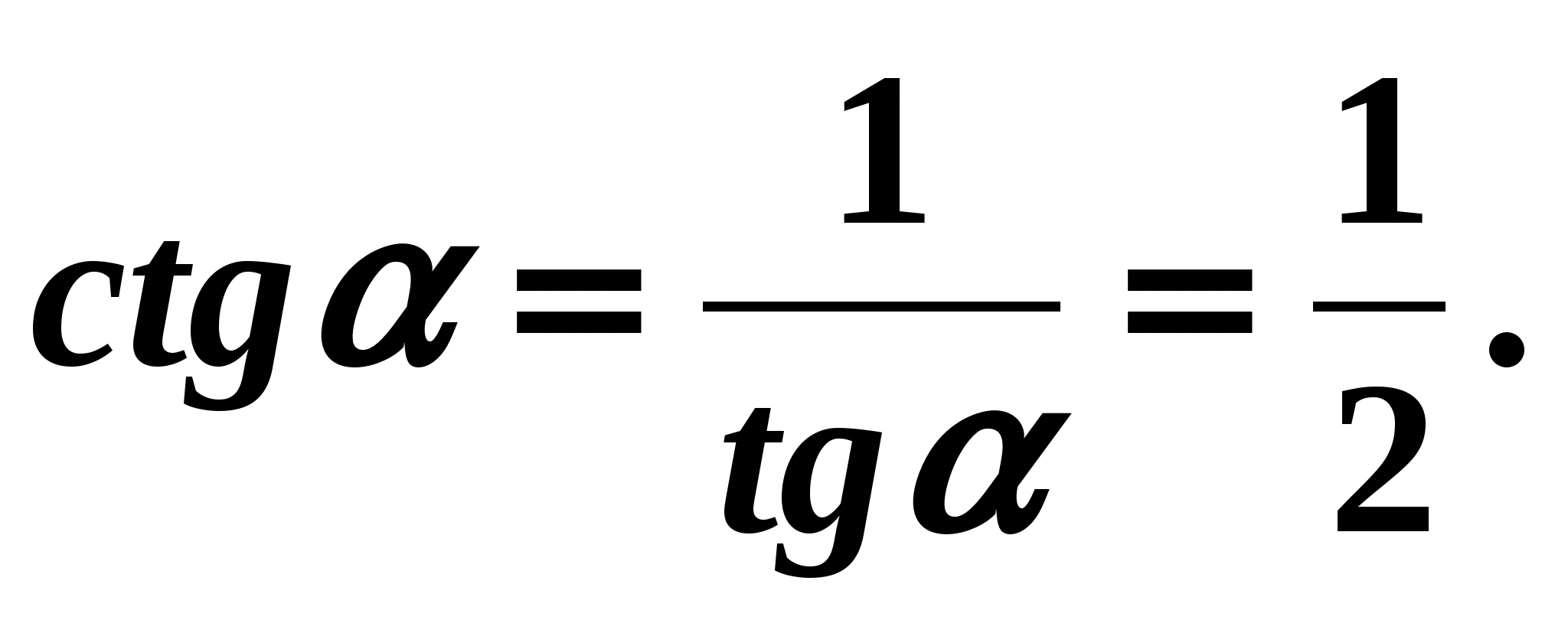
Ответ: ![]()
Установленные соотношения между тригонометрическими функциями одного и того же аргумента позволяют упрощать тригонометрические выражения.
Пример 3. Упростим выражение: ![]()
Решение: Воспользуемся формулами: ![]() . Получим:
. Получим: ![]()
![]()
-
Закрепление.
А сейчас на экране представлены рубрики самооценки по данной теме. Отметьте, на какой уровень вы бы хотели сегодня выйти.
-
Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, но с помощью наводящих вопросов (карточка – инструкция).
-
Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, используя указания преподавателя.
-
+ Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, без наводящих вопросов и указаний.
-
+ Я понял тему и могу решать примеры по алгоритму, не заглядывая в тетрадь.
Какой бы уровень вы не выбрали, сначала внимательно просмотрите все задания, которые я вам раздала, а затем выполните задание, соответствующее выбранному вами уровню (перед вами лежат задания четырех вариантов, номер варианта соответствует уровням самооценки.)
1 вариант
-
Дано:
 Найдите
Найдите 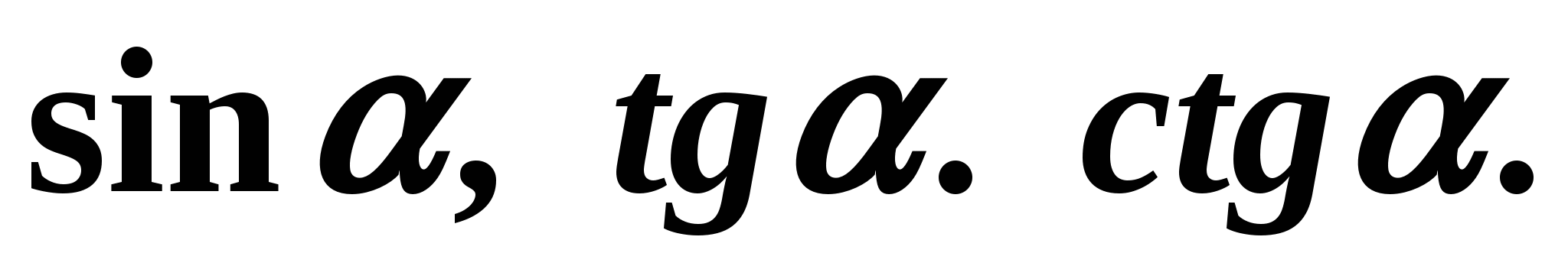
Инструкция:
-
определите четверть, в которой находится угол . Если возникают затруднения, то можно посмотреть в справочнике;
-
определите знак функции синус в этой четверти. Проверьте себя, посмотрев в справочник;
-
напишите формулу (2) из сегодняшнего урока, указав перед корнем знак, который выбрали ранее;
-
в написанное выражение подставьте значение косинуса, вспомните, как дробь возводится в квадрат (нужно возвести в квадрат числитель и знаменатель дроби);
-
выполните вычисления под корнем, извлеките корень (нужно извлечь корень из числителя и знаменателя);
-
вспомните определение функции тангенс, (можно посмотреть в справочник), запишите формулу;
-
правильно выполните деление дробей: при деление дроби на дробь, вторую дробь нужно перевернуть и дальше числитель первой дроби умножить на числитель получившейся дроби, тоже нужно сделать и со знаменателями:
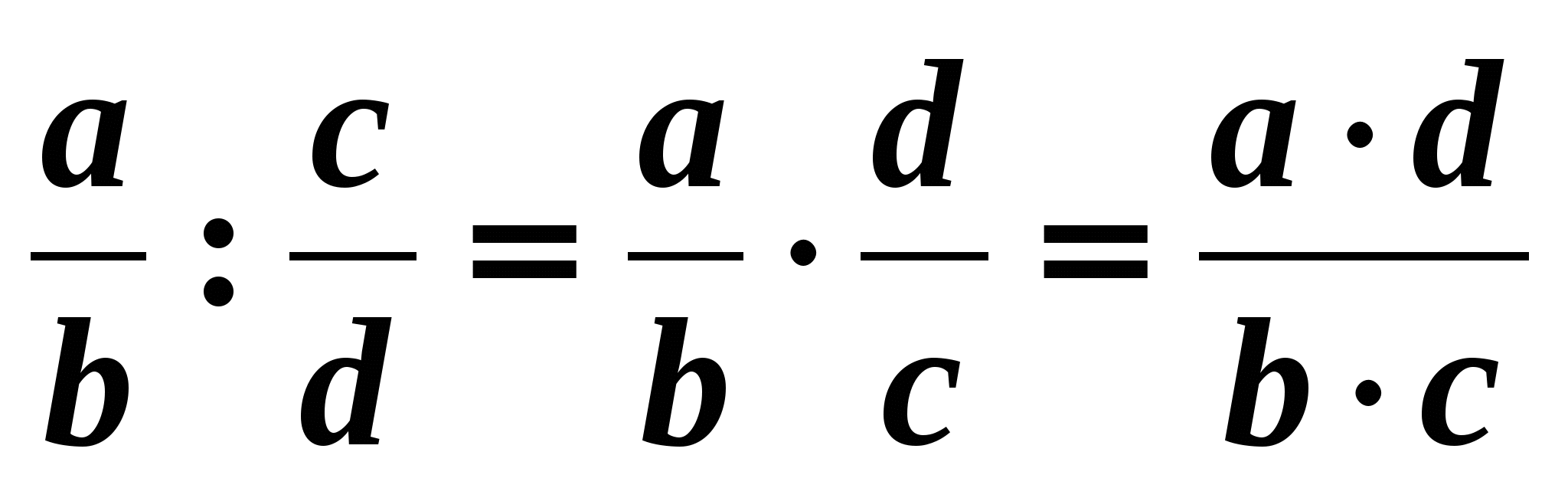 ;
; -
функцию котангенс можно найти по формуле (6) из сегодняшнего урока;
-
запишите ответ.
-
Упростите выражение:

Инструкция:
-
замените единицу равным ей выражением
 Только не забудьте, что в примере перед единицей стоит знак минус, значит у всех слагаемых изменится знак;
Только не забудьте, что в примере перед единицей стоит знак минус, значит у всех слагаемых изменится знак; -
приведите подобные;
-
запишите ответ.
2 вариант
-
Дано:
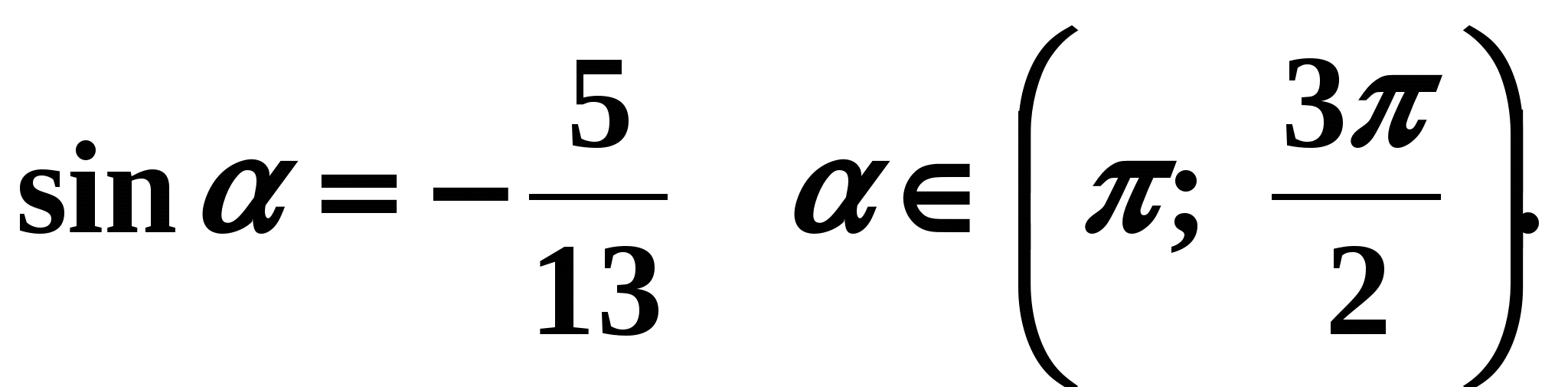 Найдите
Найдите 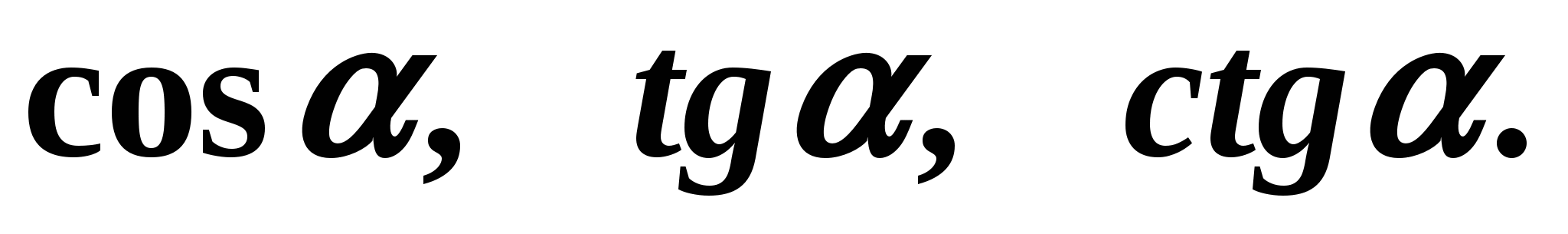
Указание: Для определения функции косинус воспользуйтесь формулой (3) из сегодняшнего урока. Не забудьте определить знак, который будет стоять перед корнем. Для вычисления значений тангенса и котангенса можно воспользоваться определением этих функций ил использовать формулы, которые мы вывели сегодня на уроке.
-
Упростите
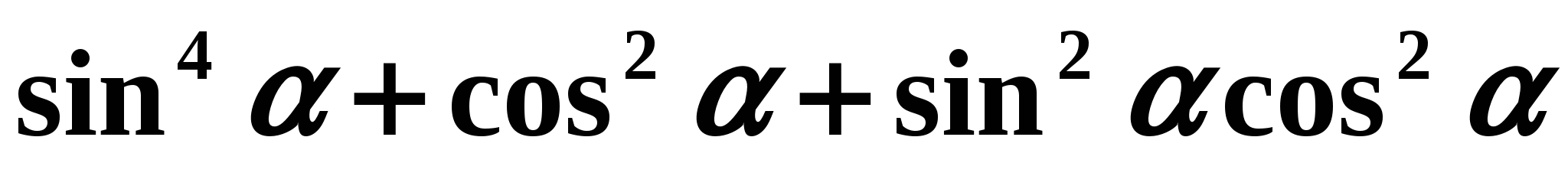
Указание. Сгруппируйте первый и третий члены выражения, вынесите за скобку общий множитель….
3 вариант
-
Дано:
 Найдите
Найдите 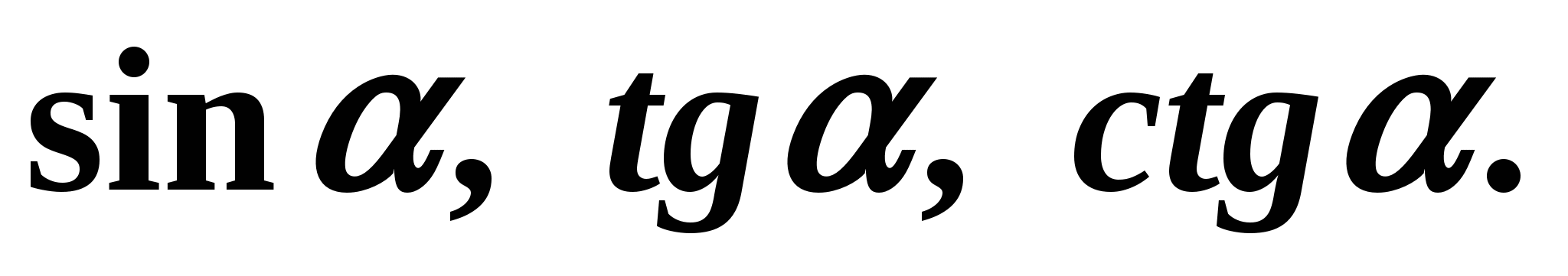
-
Упростите:

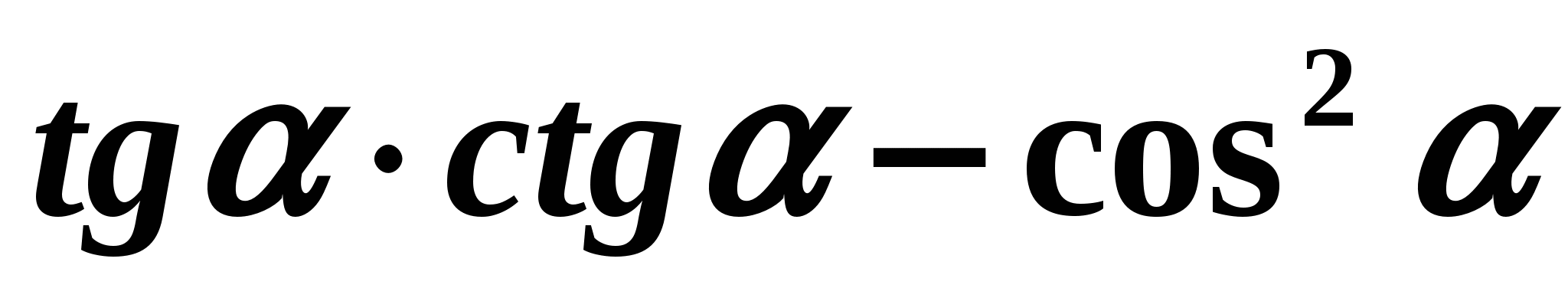 .
.
4 вариант
-
Дано:

 Найдите
Найдите 
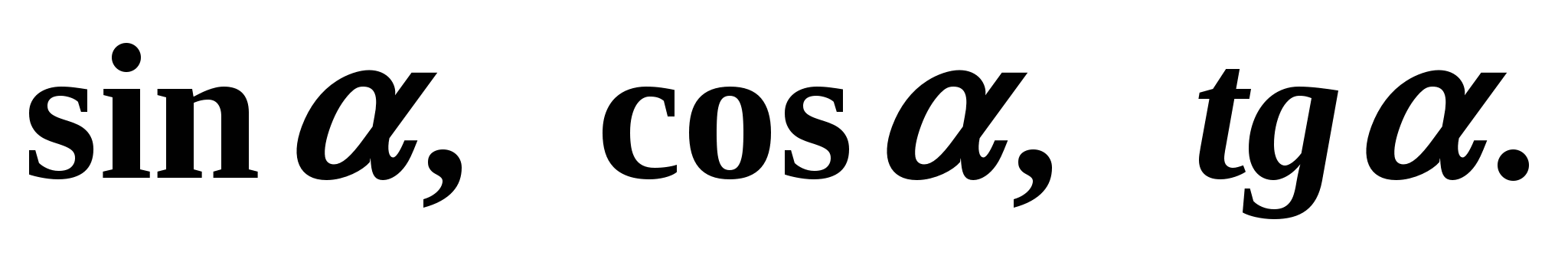
-
Упростите

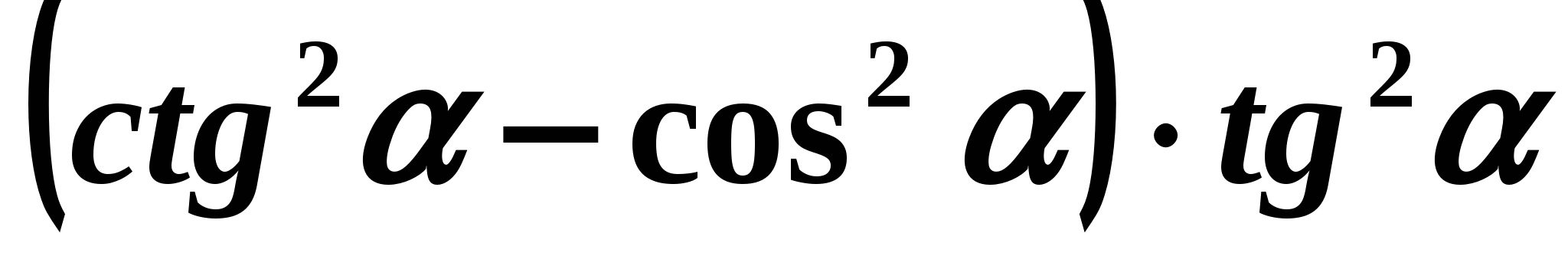 .
. 
А теперь, ребята, давайте проверим ответы. На экран выводятся правильные ответы, и учащиеся проверяют свои работы и выставляют баллы в карту урока для Задания № 4.
По карте урока оцените себя. Подсчитайте свои баллы и выставите их в карту.
-
Домашнее задание.
-
Записать все выведенные формулы в справочник.
-
По учебнику №459 (3, 5), №460 (1)
-
Здесь представлен конспект к уроку на тему «Тригонометрические формулы», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

