Конспект урока «Геометрическое применение производной»
Тема «Геометрическое применение производной»
Производная функции y = y(x) при данном значении аргумента х = х0 равна угловому коэффициенту касательной, проведенной к графику этой функции в точке с абсциссой х0 и ординатой y0 = y(x0)
y'(x0) = tg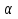 (1)
(1)
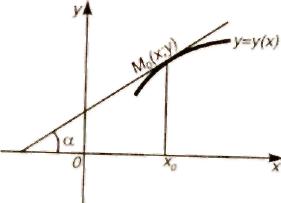
Уравнение касательной к графику функции y = y(x) в точке М0(х0; у0) имеет вид: у – у0 = y'(x0)(х – х0) (2)
Если y(x) имеет при х = х0 бесконечную производную, то уравнение касательной таково: х = х0
Уравнение нормали, т. е. прямой, проходящей через точку касания М0(х0; у0) перпендикулярно касательной, записывается в виде
у – у0 =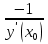 (х – х0) (3)
(х – х0) (3)
Примеры.
1. Составить уравнение касательной и нормали к параболе
у = 2х2-6х+3 в точке М0(1; -1)
Решение: Найдем производную функции у = 2х2-6х+3 при х =1. Имеем
у' = 4х – 6, откуда у'(1) = -2.
Воспользовавшись уравнением касательной к графику функции, получим искомое уравнение: у – (-1) = -2(х - 1) или 2х + у – 1= 0.
Уравнение нормали получим, используя уравнение (3)
у + 1 = 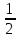 (х – 1), или х – 2у – 3 = 0
(х – 1), или х – 2у – 3 = 0
2. Составить уравнения касательной и нормали (решить самостоятельно):
а) к гиперболе у = 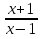 в точке А(2;3)
в точке А(2;3)
б) к кривой у = х3 + 4х2 – 1 в точке с абсциссой х0 = -1
в) к параболе у = х2 – 4х + 4 в точках, ординаты которых равны единице.
Тема «Механические приложения производной»
Производная 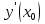 от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
В частности, если зависимость между пройденным путем s и временем t при прямолинейном движении выражается формулой s = s(t), то скорость движения в любой момент времени t есть 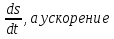 (т. е. скорость изменения скорости) есть
(т. е. скорость изменения скорости) есть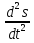
Пример.
1. Точка движется прямолинейно по закону s = 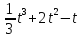 (s выражается в метрах,
(s выражается в метрах, 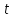 - в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
- в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
Решение:
Скорость прямолинейного движения равна производной пути по времени:
v(t) = 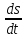 =
= 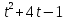 , откуда v(1) = 4 (м/с)
, откуда v(1) = 4 (м/с)
Ускорение прямолинейного движения равно второй производной пути по времени: a(t) = 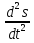 = 2t + 4.
= 2t + 4.
Следовательно, a(1) = 6(м/с2)
Решить самостоятельно следующие задачи:
2. Закон прямолинейного движения точки выражается формулой
s = 1 + 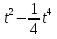 (s выражается в метрах,
(s выражается в метрах, 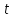 - в секундах). Найти скорость и ускорение движения в момент времени
- в секундах). Найти скорость и ускорение движения в момент времени 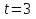
3. Тело массой 25 кг движется прямолинейно по закону s = ln(1 + 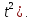 Найти кинетическую энергию тела (0.5m
Найти кинетическую энергию тела (0.5m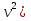 через 2с после начала движения.
через 2с после начала движения.
4. Точка движется по оси абсцисс по закону x = 0,25(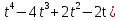
(х выражается в метрах, 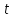 - в секундах). В какой момент времени точка остановится?
- в секундах). В какой момент времени точка остановится?
Здесь представлен конспект к уроку на тему «Геометрическое применение производной», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

