Конспект урока «Применение дифференциального и интегрального исчисления» по геометрии

Урок 6

Тема урока: «Применение дифференциального и интегрального исчисления»

Тип учебного занятия:

Обобщение и систематизация знаний учащихся.

Цели урока:

Организовать деятельность учащихся по обобщению и систематизации знаний учащихся в рамках темы.

Обеспечить проверку и оценку знаний и способов действий, выявить типичные ошибки и пробелы в знаниях учащихся с целью их устранения.

Создать условия для развития у учащихся умений структурировать информацию, приобщать к чтению научно-популярной литературы, формировать умения выделять главное, существенное, логически верно излагать материал.

Способствовать воспитанию самостоятельности, воли, умения преодолевать трудности.

Рекомендуемая литература для учащихся:

- «История математики в средней школе» Г.И.Глейзер;

- Энциклопедический словарь юного математика;

- Учебники «Алгебра и начало анализа»

Ход урока.

I. Организационный момент.

Преподаватель объясняет цель и задачи урока.

II. Актуализация знаний учащихся.

1. Фронтальный устный опрос.

- То такое производная?

- Геометрический и механический смысл производной.

- Какие практические задачи можно решить с помощью производной?

- Что такое интеграл?

III. Этап обобщения и систематизации знаний и способов действия.

Из истории дифференциального исчисления. (Сообщение учащегося).

Раздел математики, в котором изучаются производные и их применеиние, нзывается дифференциальным исчислением. Приращения вида  представляющие собой разности, играют заметную роль при работе с производными. Естественно, поэтому появление латинского корня differentia (разность) в нзвании нового исчисления. Это название появилось уже в конце XV века, т.е. при рождении нового меттода. Термин «производная» является буквальным переводом на русский язык французского слова derivec,которое ввел в 1797 году Ж.Лагранж (1736-1813гг.), он ввел современное обозначение y’и ‘.

Такое название отражает смысл понятия: функция ’(x) происходит от (x) и является производным от (x) «получается от нее».И.Ньютон называл производную функцию «флюксией», а саму

функцию - «флюентой». Лейбниц говорил о дифференцильном отношении, обознчал прроизводную как 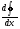. Это обозначение так же часто встречается в современной литературе. Дифференциальное исчисление создано Ньютоном и Лейбницем срвнительно недавно, в конце XVII века. Тем более поразительно, что задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумель нйти максимум функции (x) = x² (a –x). Эпизодически понятие касательной, которое связано с понятием производной, встречалось в работах итальянского математика Н. Ортальи (1500-1557гг.). Здесь касательная появилась в ходе изучениявопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полет снаряда. И.Кеплер рассматривал касательную в ходе решения задачио наибольшем объеме параллепипеда, вписаного в шр данного радиуса. В XVII веке на основе учения Г.Галилея о движении активно развилась кинетическая концепция производной. Различные врианты изложения, примененные к разным задачам, встречаются уже у Р. Декартье, французского математка Роберваля (1602- 1677гг) и, наконец, в работах И.Ньютона.

Систематическое учение о прроизводных развито Лейбницем и Ньтоном, который сформулировал две основные проблемы анализа:

1. Длина прямого пути постоянная (т.е. в любой момент времени). Дана S(t) т. Требуется найти скорость V (t) движения в предложенное время.

2. Скорость движения постоянна Требуется найти длину пройденного в предложенное время пути

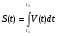
Первая первообразная здает программу развития дифференциального исчисления. Вотря проблема относится к интегрльному исчислению. Если Ньютон исходил в основном из здач мехники (Ньютонов анализ развивался одновременно с ньютовской классической механикой), то Лейбниц по преимуществу исходил из геометрических задач. Говоря о последнем развитии идей анализа (а они очень быстро завоевали популярность и нашли много последователей) следует в первую очередь назвать имена учеников Лейбница – братьев Я. и И. Бернулли. Лопиталь (1661-1704гг), который учился у И.Бернулли и издал уже в 1696 году первый печатный корпус дифференциального исчисления «Анализ бесконечно малых для исследования кривых линий».

Интегральное исчисление

Дифференцирование и интегрирование (нахождение производной и первообразной) – действия математического анализа.

В отличии от действий над числом в алгебре (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, логарифмирование) это действия над функциями, позволяющие найти:

- с помощью производной: закон изменения скорости роста функции.

- с помощью первообразной – изменение площади фигуры, находящейся под графиком функции.

Конкретные функции использовались в математике еще в глубокой древности. Сам термин «функция» впервые применил Лейбниц, а его ученик И. Бернулли в 1712 году дал определение близкое к тому, которым мы пользуемся.

Почти все действия, существующие вокруг нас, описываются функцией.

S =V t – закон равномерного движения, где S – путь, t – время, V – скорость.

S = 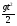закон свободного падения.

q = C U –уравнение заряда конденсатора.

Е = 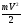- кинетическая энергия материальной точки.

V= 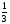п R²H – объем кругового конуса и т.д..

Применение производной и интеграла.

Механический и геометрический смысл производной.

1. Механический смысл производной.

Механическй смысл производной – это нахождение закона изменения скорости по известному закону движения. Дано S (t), находим V (t) =S’(t) по данной функции находим мгновенную скорость, задавая любое время.

Обратная задача: По известному закону скорости находим закон изменения рассттояния, что предполагает

интегрирование.

Дано: V (t), находим 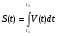и вычисляем пройденный путь з промежуток времени от t₁ до t₂ , где V (t) – изменяющаяся скорость.

Задачи:

1. Водитель автомобиля, заметив на дороге пешехода на расстоянии 9м, начал экстренное торможение. Скорость автомобиля на момент торможения 28,8 км/ч. При торможении скорость автомобиля менялась за 1с на 4 м/с. Успеет ли водитель остновить автомобиль?

2. Из пункта А, находящегося в поле в 5км от прямолинейной дороги, автомобиль ГАЗ-53 должен вывести свеклу в пункт В, расположенный у дороги в 13 км от пункта А (по прямой). По дороге автомобиль, загруженный свеклой, едет со средней скоростью 50км/ч, а по полю -30км/ч. На кком расстоянии от пункта В водителю выгоднее выехть на дорогу, чтобы время, пройденное в пути было наименьшим?

3. Тело движется прямолинейно с ускорением a(t)= 12t² + 4. Найти закон движения точки, если в момент t=1, скорость равна 10 м/с, а расстояние равно 12 (а- измеряется 1м/с)

Одной из характеристик движения является скорость. Скорость бывает средней, когда все пройденное расстояние делим на весь промежуток времени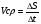

Пример: за 2 часа автомобиль прошел 150 км найти среднюю скорость:

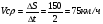
Средняя скорость не может полно охарактеризовать движение, не может сказать, как двигателя автомобиля?

Есть еще скорость – скорость мгновенная.От нее зависит решение многих практических задач.

Например, от скорости вхождения в воду прыгающего с вышки спортсмена, зависит глубина его погружения.

От скорости запуска спутника зависит выход его на заданную орбиту.

Наконец, мгновенная скорость дает почти полную характеристику движения автомобиля (с некоторой погрешностью на практике это делает спидометр)

Мгновенная скорость – это скорость в данный момент времени.

При ее нахождении берется бесконечно малый промежуток времени и бесконечно малый путь, пройденный за это время.

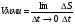-это предельное отношение пройденного пути к

бесконечно малому промежутку времени и есть производная пути по времени

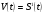
Впервые задачу на хождения мгновенной скорости решил английский ученый Исаак Ньютон в конце XVII века. Оказалось, что связь между количественными характеристиками самых различных процессов, исследуемых физикой, химией, биологией, техническими науками, аналогична связи между путем и скоростью.

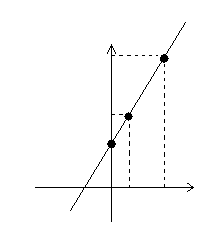
Пример: пусть пройденный телом путь изменяется по закону 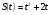(пусть функция времени) графически:

t

S(t)=t²+2t

V(t)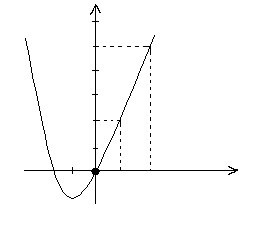

t

0	1	2	3	(с)
S(t)	0	3	8	15	(м)

из графика видно, что за одинаковый промежуток времени тело проходит разные расстояния, т.е. его скорость меняется.

Закон изменения скорости позволяет найти производная: V(t)=S¹(t)=(t²+2t)¹=2t+2

V(t)= 2t+2 график скорости:

t¹

0	1	2
V(t)	2	4	6

V(t)=2t+2

t

V

по данной формуле V(t)=2t+2 (как и по графику) можно найти скорость в любой момент времени найти скорость в любой момент времени V(t)=4м/с V(2)=6м/с и т.д.

Итак скорость – это производная пути по времени

V(t)=S¹(t). x0,

При нахождении мгновенной скорости используется средняя скорость движения за малый промежуток времени.

Пусть точка движется вдоль прямой и за время t от начала движения проходит путь S(t)

S₂

S

S₁

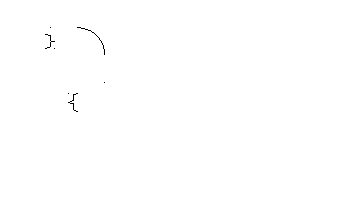
t₁

t₂

t

t₂ - t₁= t – время движения

S (t₂) – S (t₁) = S – пройденный путь

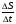= V ср.

если t 0, то lim 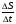= V = V(t₀) – скорость в данный момент времени.

Предельное отношение: lim 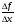= f ‘ (x) – производная функция.

Значит, если задан закон движения S(t) , то мгновенная скорость V(t)= S’(t) (производная пути по времени)

Пример:

Пусть S(t) = t ²+2t t

S

0 1 2 3 (м)

0 3 8 15 (c)

-2 -1 0 t

ТоV (t)= S’(t) = (t²+2t)’ = 2t +2

t

V

0

1

2

5

3

7

V

t

V (t) =2t +1-закон изменение скорости, по которому можно нйти скорость в любой момент времени.

Решите задачу 1.

Автомобиль должен остановиться за 8 м до начала торможения. С какой скоростью он должен подойти к тормозящей отметке, если дальше он двигается равнозамедленно с ускорением -4 м/с².

Дано: S _{торм. n}= 8м

a= - 4м/с²

Найти:V на момент начала торможения.

Решение: V= at, t- время торможения.

I ускоренное движение: S(t) = 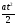; 8= 2 t²; t = 2 (c).

2. V= 4 2 =8 м/с – на момент начала торможения скорость автомобиля была 8 м/с.

Ответ: 8 м/с

Решите задачу 2.

Водитель автомобиля, заметив на дороге пешехода на расстоянии от него 9м, начал экстренное торможение, скорость автомобиля на момент начала торможения 28,8 км/ч.

При торможении скорость автомобиля менялась за 1 с на 4 м/с. Успеет ли водитель остновить автомобиль?

S (t) =V₀t +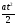

28,8км/ч = 8 м/с

Остановка: V (t) =0

V (t) =S’(t) = (8t-2t²)’ = 8- 4t

8-4t =0; t = 2 (c)

S(2)= 82 -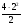=8м/с

Водитель успеет остновить автомобиль.

2. «Геометрический смысл производной»

Честь открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Готфриду Лейбницу.

К этим законам Лейбниц пришел, решая задачу проведения касательной к произвольной кривой.

Y

касательная

a

Y

X

секущая

X

Y₂

Y₃

B

A

N

X₁

X₂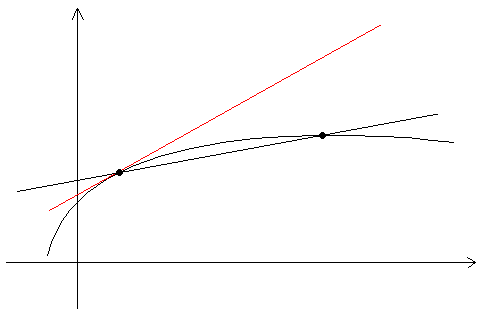

Пусть дана функция f(x) необходимо узнать под каким углом в т. А к ней может быть проведена касательная.

Для секущей эта задача решаема несложно: секущая АВ. Точка A (x₁;y₁); B (x_2;y₂)

Из  ABN можно найти tg.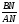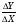 ==; Y= Y₂- Y₁; X=X₂-X₁;

tg – это угловой коэффициент прямой tg=k

Итак, k_сек.=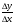

Для касательной: передвигаем т.В по графику к точке А при этом:

секущая переходит в касательную

x₂x₁; x0 тогда

Угловой коэффициент касательной k_кас.= tgв будет равен предельному отношению y к x , k_кас.= lim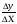 т.е. производной f”(x₀) – 8 x0,

k_кас.= lim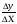= f”(x₀)

Итак, производная функции позволяет найти закон изменения угловых коэффициентов в различных точках функции. А зная угловой коэффициент k_кас найдем tgв, и далее сам угол в

k_кас= tgв= f”(x₀), тем самым мы можем узнать скорость роста функции.

Задача 3 : найти угол наклона касательной к параболе y=x² в т.x₀=2

Решение: 1) находим закон изменения углового коэффициента всех касательных, скользящих по параболе y=x², k= f”(x) =y”(x²) ”= k_кас= 2x

k_кас=2x

2) в точке x₀ =2, k_кас=22= 4 ; k_кас= tgВ; tgВ= 4, в = arctg476⁰

Зная закон изменения касательных для данной функции мы можем судить о скорости ее роста: чем больше в, тем быстрее растет функция.

Причем: если k= f”(x) =0 (касательная параллельна оси x)

если k= f”(x) 0, то сама функция возрастает

если f”(x)  0, то сама функция f(x) убывает

Значит: с помощью производной мы можем строить графики различных функций, зная точки max, min, перегиба, промежутки возрастания и убывания, что является одним из главных свойств функции.

Применение производной.

Физика

С помощью производной можно решить множество задач по физике.

• Можно определить выполненную рботу в днной точке, если известно изменение силы приложенной к телу при его перемещении.

A = F’(x) или dA = Fdx (на малом отрезке dx )

• Можно определить величину заряда, переносимого электрическим током через поперечное сечение проводника в данный момент времени при изменяющейся силе тока I.

q = I’(t) dq = Idt

• Можно определить массу тонкого стержня (неоднородность). Линейная плотность – это прроизводная массы по длине.

P (l) = m’(l)

Все приведенные примеры построены по одному и тому же образцу. В каждом примере речь идет о связи между тремя величинами, уже знакомыми из курса физики: работа, перемещение, сила, заряд и т.д. Во всех примерах одна из величин выступает как функция другой, и каждый раз появляются соотношения вида K=y’(x), т.е. все задачи решаются с помощью нахождения производной.

Большую часть своих усилий человек тратит на поиск наилучшего, или как часто говорят, оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добитться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальных зтрат времени- так ставятся вопросы, над которым приходится думать каждому члену общества. Не все такие задач поддаются точному математическому описанию, не для всех из них найдены короткие пути решения. Однако, часть таких задач поддаются исследованию с помощью методов мтемтического анализа – это задачи, которые можно свести к нахождению наибольшего или наименьшего значения функции.

Задача: Из пункта А, находящегося в поле в 5 км от пряиолинейной дороги автомобиль ГАЗ -53 должен вывести свеклу в пункт В, расположенный у дороги в 13 км от пункта А по прямой

3. Для каждого действия есть противодействие.

Обратное действие для нахождения производной – нахождение первообразной (интегрирование).

1.Общее понятие первообразной (механический смысл первообразной).

Рассмотрим равномерное движение, т.е. движение тела с постоянной скоростью V(t)-const(константа) когда S=V*t – пройденное расстояние, путь:V(t)=4м/с. Найти 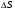за время от t₁=0 до t₂=5м

V

V(t)=4

4

5

0

t

5

Расстояние - площадь подграфика - первообразная - (определенный интеграл)

Под графиком скорости получился прямоугольник S_{прямоуг}=a*b=4*5=20(кв.ед.)

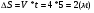
Значит, путь пройденный телом в графическом изображении сравнима по величине с площадью фигуры под графиком скорости.

Задача 4.

Тело движется со скоростью меняющейся по закону V(t)=2t+2

t

0	1	2	3
V(t)	2	4	6	8

Найти путь, пройденный телом от t₁=1c до t₂=3с

Под графиком скорости V(t) лежит трапеция

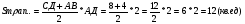
Механический и геометрический смысл первообразной

Механический смысл первообразной.

Если для применения производной мы рассматриваем Vмгн .= S¹(t), т.е. дан был закон изменения расстояния, а мы находили закон изменения скорости, то для первообразной становится обратная задача:

дан закон изменения скорости V(t) найти путь, пройденный телом за время от t₁ до t₂, т.е. найти закон движения S(t)

Задача: Скорость движущегося тела меняется по закону V(t)=2t+2 найдите каков путь пройдет тело при движении от 1с до 3с, т.е. за 2с.

Решение: 1) найдем закон перемещения, то есть первообразную для функции V(t)=2t+2:

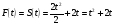
2) при t=1c; S(1) = 1² + 2*1 =3 (м)

при t=3c S(3) = 3² + 2*3 = 9 + 6 = 15 (м)

тогда пройденный путь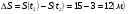

Интеграл и его применение.

Задача. Определите массу стального обода рулевого управления автомобиля ЗИЛ-130, который представляет собой шар, имеющий диаметр поперечного сечения d₀=1см и наружный диаметр d= 48 см.

Y Решение:

Площадь круга, являющегося поперечным сечением обода, можно рассматривать как разность площадей трапеций

P АССВВ₁А₁ и ОВВ₁А_2..

X

А₁

В₂

X

r

r

Y

С O

Д

Дуге АСВ соответствует уравнение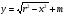

Уравнение окружности x² +y²=r²

Дуге АДБ соответствует уравнение 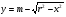, где r-OC, m = 0,01

Значит объем тора:

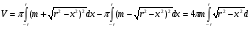
Применение интеграла.

Задача. Скорость движения меняется по закону V(t) = 2t (скорость в метрах в секунду). Найдите длину пути, пройденного телом за третью минуту его движения.

Решение: ;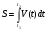

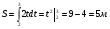
Задача 2. Скорость движения тела меняется по закону V=3t² +t +1 (скорость в м/с). Найдите путь, прройденный телом за 4с от начала движения.

Решение: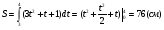

Задача 3. Тело брошено вертикально вверх со скоростью, которая изменяется по закону V(t) = 29,4 – 9,8 t (скорость в метрах в секунду). Найдите наибольшую величину подъема.

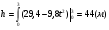
Задача. Найдите длину пути, пройденного телом от начала движения до остновки, если его скорость изменилсь по закону V (t) =4t – t² м/с

Решение: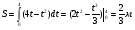

Работа силы.

Сила сопративления Fсопр. (кН) движению трактора от деформации снега определяется формулой 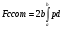, где b- ширина гусеницы (м), h – глубина колеи (м), - удельное давление опорной поверхности на снег.

Задача. Определите силу сопративления движению трактора от деформации снега:

- Для трактора ДТ-75 при глубине колеи 0,2 м

- Для трактора Т -150 при глубине колеи 0,3 м

Решение: 1 мПа= 10⁶Па

Из справочника:

ДТ-75	Т-150
Масса трактора	6370 кг	7030 кг
Удельное сопративление	0,044 мПа	0,046 мПа
Ширина гусеницы	390 м	390 мм

Работа силы. Если на тело движущееся по прямой действует сила, тогда в зависимости от силы меняетсярасстояние.

А – работа, A=FS , Изменение работы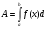

Задача. Сила в 10 Н растягивает пружину на 2см. Какую работу она при этом совершит?

Решение:

По закону Гука F=kx, где

F –сила, растягивает пружину

K - коэффициент упругости

X – растяжение

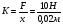= 500 Н/м, значит F(x)=500 x; растяжение от x₁=0 до x₂=2 см= 0,02м

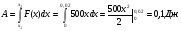
1. Сила в 60 Н достаточна, чтобы растянуть пружину на 2см. Первоначльная длина пружины 14 см. Какую работунадо совершить, чтобы растянуть ее до 20 см?

Решение:

По закону Гука F=kx,

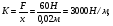тогда F(x) = 3000x

растяжение x₁ =14 см = 0,14 x₂= 20 см= 0,2м

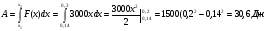
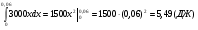
Задача.Рессоры прогибаются под действием силы.

Какую работу надо затратить для деформации рессоры на 3см? (деформирующая сила пропорциональна прогибу рессоры)

Решение:

F=kx, где x - прогиб рессоры.

При x =1см =0,01м имеет k=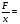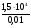= 1,510⁶

Отсюда: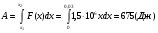

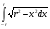выражает площадь полукруга радиуса r

Следовательно, V тора =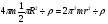

Подставляя значение m= 23,5 см,

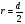=0,5 см

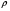стали = 7800 кг/м³

Находим, что масса обода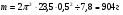

Ответ:904г.

Первообразная (геометрический смысл)

В

С

Д

А

t

2

4

6

2

8

V(t)=2t+2

Получаем, что с помощью первообразной можно найти пройденный путь, что равняется площади под графиком или криволинейной трапеции.

а

в

y

F(x)

x

для f(x)

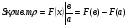- это формула носит название формула Ньютона-Лейбница.

Само слово «первообразная» состоит из двух слов «первый образ».

Первый образ функции до того, как была найдена производная.

F(x)- первообразная для функции f(x), если F¹(x)=f(x).

V.Подведение итогов

Общая оценка работы учащихся в группе, рекомендации учащимся по ликвидации выявленных пробелов в знаниях.

Оценка за практическую работу

VI. Рефлексия.

Вывод учащихся по проделанной работе, их самооценка и пожелания преподавателю.

Каждый учащийся определяет свою точку по степени усвоения материала данного урока и на оценочных листах проставляют свои точки

const

max₁

max₂

min₁

min₂

Min₃

1. const – урок как урок

2. min₁ – «не понял!»

3. min₂ – не все понял, но хочу понять

4. max₁ – не все понял, прошу помощи!

5. max₂ – понял!

6. Min₃ – не хочу понимать!