Конспект урока «Медиана, биссектриса и высота треугольника» по геометрии

Автор: Добриян Валентина Васильевна

учитель математики

Лингвистическая школа- лицей

Материал скачан со страницы: http://pedsovet.su/load/136-1-0-8996

ТЕМА: Медиана, биссектриса и высота треугольника

Цели:

а) образовательные – ввести понятия медианы, биссектрисы и высоты треугольника; научить строить медианы, биссектрисы и высоты треугольника.

б) развивающие – постановка и развитие правильной математической речи, способствовать развитию умения анализировать, сравнивать, устанавливать причинно- следственные связи, интерес к предмету;

в) воспитательные – прививать аккуратность, ответственность и уважение к одноклассникам, умение слушать, отстаивать свое мнение.

Основные термины и понятия: медиана, биссектриса, высота.

Планируемые результаты обучения: уч-ся должны знать определение медианы,

биссектрисы и высоты треугольника, уметь их использовать при решении задач и доказательстве признаков равенства треугольников.

Тип урока: изучение и первичное запоминание новых знаний и способов деятельности

Класс: 7

Ход урока

I. Организационный этап.

II. Актуализация знаний.

Работа по готовым чертежам.

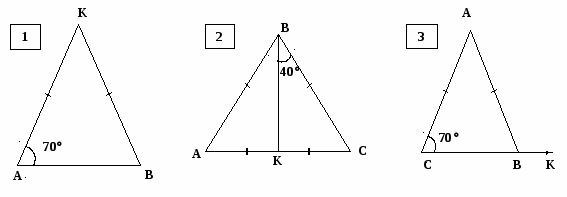
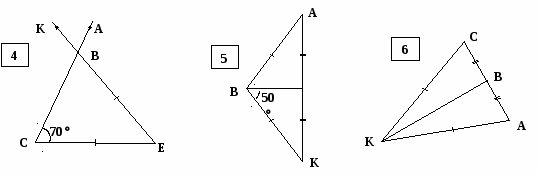
Найти угол КВА. Чертежи на рисунках 3, 4, 6 – в тетрадь (задания – на карточке).

C

III. Формирование новых понятий и способов действия

О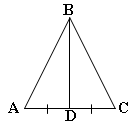пределение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BD- медиана АВС, если AD=DC, где DАС.

В равнобедренном треугольнике медиана, проведенная к основанию является биссектрисой и высотой.

О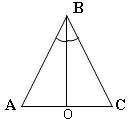пределение. Отрезок, соединяющий вершину угла с противолежащей стороной и делящий угол пополам, называется биссектрисой.

ВО- биссектриса АВС, если АВО=СВО, где ОАС

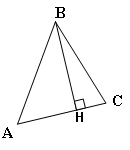
Определение. Перпендикуляр, опущенный из вершины угла на противоположную сторону, называется высотой.

ВН- высота АВС, если ВНАС, НАС

IV. Практическая работа.

Для закрепления навыков построения учащиеся выполняют следующие задания.

Задание 1. Начертить любой треугольник, дать ему название и провести всевозможные медианы, сделать соответствующие записи.

Задание 2. Начертить любой треугольник, дать ему название и провести всевозможные биссектрисы углов, сделать соответствующие записи.

Задание 3. Начертить три вида треугольников (прямоугольный, остроугольный, тупоугольный), дать им название и провести всевозможные высоты, сделать соответствующие записи.

V. Применение. Формирование умений и навыков.

Решить задачу:

В равнобедренном треугольнике АВС с основанием ВС проведена медиана АD. Найдите длину медианы АD, если периметр треугольника АВС равен 32 см, а периметр треугольника АВD равен 24 см.

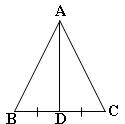
Дано: АВС- равнобедренный

АD- медиана

Р_АВС=32 см

Р_АВD=24 см.

Найти: АD

Решение:

1. Р_АВС=АВ+ВС+АС=32 см. Так как АВ=АС, BD=CD, то ВС= 2BD и Р_АВС=АВ+2BD+АВ=2(BD+АВ)= 32 см, отсюда следует, что BD+АВ=16 см.

2. Р_АВD=(АВ+ BD) + АD= 24 см. Отсюда следует, что АD=24 см-16 см = 8 см.

Ответ: АD=8 см.

С 57 № 185, 188, 192

VI. Домашнее задание :

С 57 № 191, 193

VII. Подведение итогов урока : выставление оценок, выявление лучшего, поощрение отдельных учащихся и т. п.