Конспект урока «Теорема Пифагора. Решение задач» по геометрии для 8 класса

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа с. Липовка Духовницкого района Саратовской области»
Урок геометрии с использованием ИКТ.
Выполнила учитель первой
квалификационной категории
Евсеева Е. М.
2010 – 2011 учебный год
Тема: Теорема Пифагора. Решение задач.
Класс: 8.
Форма проведения: Урок – изучение нового материала.
Цели урока:
-продолжить овладение системой геометрических знаний и умений, необходимых для продолжения образования;
-воспитать отношение к геометрии как к части общечеловеческой культуры, понимание значимости геометрии для научно-технического прогресса;
-развивать умение классифицировать информацию, используя разнообразные информационные источники.
Задачи:
-развивать логическое мышление, интуицию путем устного решения геометрических задач;
-учить ясно, точно, грамотно излагать свои мысли в устной и письменной речи;
-проводить доказательные рассуждения;
-приобретать опыт исследовательской работы;
-развивать умение работать в коллективе.
Оборудование:
-
Компьютерный класс.
-
Видеопроектор.
-
Портрет Пифагора.
-
Презентации детей
-
Рисунки к устным задачам.
Программное обеспечение: MS Office PowerPoint
План урока:
-
Организационный момент.
-
Актуализация знаний.
-
Сообщения детей:
а) Сообщение учащегося о жизни Пифагора Самосского;
б) Способы доказательства теоремы Пифагора;
в) Пифагоровы треугольники.
4. Работа над теоремой.
5. Решение задач с применением теоремы.
6. Итоговый контроль. Тестирование.
7. Подведение итога урока.
8. Домашнее задание.
Ход урока:
-
Организационный момент.
1 слайд. Теорема Пифагора.
Учитель: «Тема нашего урока «Терема Пифагора». Мы познакомимся с еще одной новой теоремой, узнаем, чье имя она носит, рассмотрим ее доказательство и научимся применять ее при решении задач. Чтобы подготовиться к этой работе решим устно задачи».
-
Актуализация знаний.
2 слайд.
Дан рисунок к задаче № 1и записано ее условие:
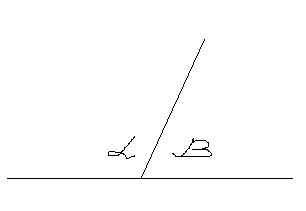
α = 3β
•Ученик объясняет решение задачи и напоминает свойство смежных углов, которое здесь используется.
3 слайд
На экране появляется рисунок задачи № 2: три угла образуют развернутый угол, сумма α и γ углов равна β. Найти β угол.
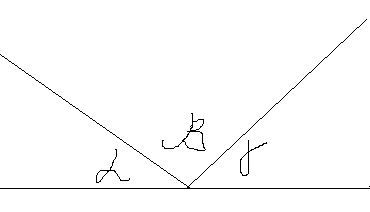
α + γ = β
•Ученик доказывает, что угол β является прямым.
4 слайд
На экране задача № 3: Определить вид четырехугольника АВСD.
•Ученик доказывает, что АВСD - квадрат.
Учитель: Эти задачи помогут нам доказать теорему Пифагора. Давайте сначала послушаем ребят. Они нам приготовили сообщения».
5 слайд
3. Сообщения детей:
а) Сообщение о жизни Пифагора Самосского;
Ученица кратко рассказывает биографию Пифагора. (презентацию готовила группа учащихся)
б) Способы доказательства теоремы Пифагора;
Второй ученик рассказывает из истории теоремы Пифагора:
-ее различные формулировки;
-способы доказательства;
-старинную ученическую формулировку теоремы.
в) Пифагоровы треугольники.
Презентация о различных видах прямоугольных треугольников
Ребята заранее приготовили презентации, которые показывают всему классу.
Учитель: «И так, о какой же геометрической фигуре сегодня пойдет речь?»
- Учащиеся отвечают, что о прямоугольном треугольнике.
Учитель: «Нарисуйте прямоугольный треугольник у себя в тетради».
4. Работа над теоремой.
6 слайд.
На экране – прямоугольный треугольник с катетами а и b и гипотенузой с.
Учитель предлагает продолжить катеты: катет а - на длину b, а катет b - на длину а. Ученики выполняют эту работу в тетради, а на экране появляется новый рисунок. Ученики объясняют, почему эту фигуру можно достроить до квадрата и выполняют это в тетради. Такой же рисунок появляется на экране.
Учитель: «Найдем площадь квадрата».
Ученики записывают в тетрадях, комментируют; на экране появляется запись (формула площади квадрата со стороной (a+b))
Вспоминая устные задачи, ученики разбивают квадрат на 5 частей и объясняют, что площадь квадрата можно найти как сумму площадей этих частей. В тетрадях и на экране - запись: площадь квадрата равна сумме 4 площадей треугольников и площади малого квадрата.
Сравнивая два равенства, делаем вывод: сумма квадратов катетов a и b равна квадрату гипотенузы с.
Вывод: Мы установили связь между гипотенузой и катетами прямоугольного треугольника. Это и есть теорема Пифагора. Учащиеся дают словесную формулировку теоремы: «В прямоугольном треугольнике квадрат гипотенузы равен суме квадратов катетов».
Учитель: «Какие задачи можно решать, применяя эту теорему?»
• Можно найти гипотенузу треугольника, зная его катеты.
• Можно, зная один катет и гипотенузу, найти другой катет.
5. Решение задач с применением теоремы.
7 слайд
Можно найти гипотенузу треугольника, зная его катеты.
Задача № 483 (а) из учебника. Ребята решают вместе с учителем на доске.
Можно, зная один катет и гипотенузу, найти другой катет.
Задача № 484 (а) из учебника. Ребята решают вместе с учителем на доске.
8 слайд. Задача № 487 из учебника.
На экране появляются чертеж и условие задачи: треугольник ABC – равнобедренный, боковая сторона равна 17 см, основание 16 см. Найти медиану треугольника.
Учащиеся самостоятельно решают задачу в тетради.
9 слайд.
Итоговый контроль: Тесты из Интернета.
| К каким треугольникам можно применить теорему Пифагора? | |
| | Любым |
| | Прямоугольным |
| | Равнобедренным |
| Чему равна гипотенуза прямоугольного треугольника, катеты которого равны 6см и 8см? | |
| | 10см |
| | 14см |
| | 2см |
| Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы? | |
| | Нет |
| | Не знаю |
| | Да |
| Гипотенуза прямоугольного треугольника равна 5см, катет 3см. Найти длину второго катета? | |
| | 8см |
| | 4см |
| | 10см |
10 слайд
Проверка результатов тестирования.
11 слайд
Подведение итога урока.
Учитель: «С какой теоремой мы сегодня познакомились? Дайте ее формулировку».
(ответы учащихся)
Учитель: «При решении каких задач она применяется?»
(ответы учащихся)
Учитель: «Зачем нам нужна теорема Пифагора?»
Учащиеся высказывают свое мнение, и учитель предлагает им к следующему уроку изложить свои мысли в виде мини-сочинения.
12 слайд.
Домашнее задание: теоретический материал по учебнику, задачи №483 (б),№484 (б), № 488 из учебника, мини-сочинение на тему «зачем нужна теорема Пифагора?»
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Конец формы
Здесь представлен конспект к уроку на тему «Теорема Пифагора. Решение задач», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

