Конспект урока «Теорема Пифагора» по геометрии для 8 класса

Урок геометрии в 8-м классе: "Теорема Пифагора"

Цели урока:

Образовательная:

• обеспечить понимание доказательства теоремы Пифагора и ее применение к решению задач.

Развивающая:

• поставить учащихся перед необходимостью получения новых знаний,

• показать, что новые знания могут быть   следствием ранее изученной закономерности и развивать математическую речь, умение рассуждать, сравнивать, делать выводы.

Воспитывающая:

• воспитывать аккуратность, умение слушать товарищей и учителя.

Оборудование: портрет Пифагора, переносная доска.

Ход урока

I. Вступительное слово учителя

Ребята, сегодня мы будем изучать новую тему, но прежде повторим и проверим домашнее задание.

II. Устная работа. Накопление фактов и подготовка к восприятию

Дайте определение квадрата.

Квадратом называется прямоугольник, у которого все стороны равны.

Какое определение можно дать еще квадрату?

Квадрат – это ромб, у которого все углы прямые.

Тогда скажите, какой четырехугольник будет квадратом?

Четырехугольник будет квадратом, если:

• стороны равны,

• углы прямые

Если известна сторона квадрата, что можно найти?

Если известна сторона квадрата, то можно найти площадь.

Чему равна площадь квадрата?

Площадь квадрата равна квадрату его стороны.

Сторона квадрата равна 11 см. Чему равна его площадь?

Рис. 1

11² = 121 (см²)

Что означает запись а² = 144?

Площадь квадрата равна 144.

Чему равна сторона квадрата?

12.

Чему равна площадь фигуры F?

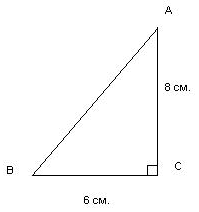
Рис. 2

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Назовите еще свойства площадей.

Равные многоугольники имеют равные площади. Площадь квадрата равна квадрату его стороны.

Сегодня мы будем говорить о правильном треугольнике. Давайте вспомним:

Рис. 3

Определение прямоугольного треугольника.

Название его сторон.

Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против угла в 90° называется гипотенузой, а две другие стороны – катетами.

Подпишите на этом чертеже другие обозначения сторон (строчными латинскими буквами).

И так, с этого момента мы будем называть стороны прямоугольного треугольника гипотенуза и катеты.

Какие свойства прямоугольных треугольников вы знаете?

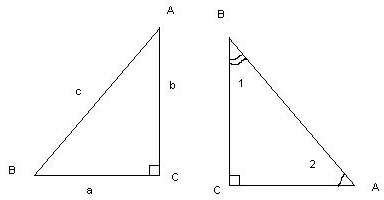
Рис. 4

Сумма острых углов прямоугольного треугольника равна 90° , т. е. A + B = 90° , 1 + 2 = 90° .

Если B = 30° , то какая существует зависимость между сторонами этого треугольника?

Катет прямоугольного треугольника, лежащий против угла в 30° ,равен половине гипотенузы.

Как на математическом языке записать эту зависимость?

АС = АВ

Правильно! Эта зависимость записывается в виде равенства. Мы знаем, что треугольники (их виды) определяются по сравнительной величине углов и сравнительной длине сторон.

О каком прямоугольном треугольнике мы еще не говорили?

О равнобедренном.

При каком условии этот треугольник будет равнобедренным?

Если катеты равны.

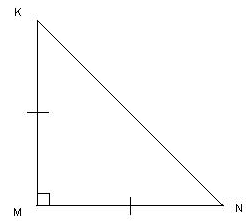
Рисунок 5

Чем интересны эти треугольники?

Острые углы равны по 45°, катеты равны.

Зная определение и свойства прямоугольных треугольников можем решать задачи. Можем? Что можете определить в этом треугольнике.

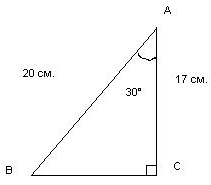
Рисунок 6

АС = 10 см.; А = 60° ; S = АC * ВС = * 10* 17 = 85 (см²).

Правильно! Площадь прямоугольного треугольника равна половине произведения его катетов.

Что можете определить в треугольнике MNK?

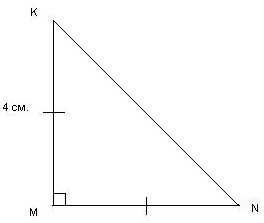
Рисунок 7

Площадь! S = * 4 * 4 = 8 (см²); N = M = 45°.

Легкие задачи? Тогда еще решим такую задачу! Что вы видите на рисунке.

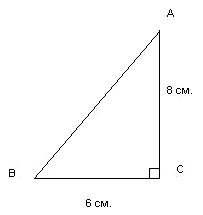
Рисунок 8

Прямоугольный треугольник с катетами 6 см. и 8 см.

Что можно определить в этом треугольнике?

Площадь. S = * 6 * 8 = 24 (см²).

Итак, АВС – прямоугольный с катетами 6 см. и 8 см. существует. Значит и гипотенузу в этом треугольнике можно вычислить. Чему же равна гипотенуза АВ?

Что известно в этой задаче?

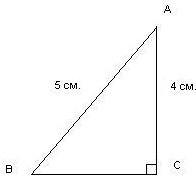
Рисунок 9

Гипотенуза 5 см. и катет 4 см. в прямоугольном треугольнике.

Вычислите площадь АВС.

Вычислить площадь нельзя!

Почему нельзя?

Катет ВС не известен.

На какие вопросы мы должны ответить в этой задаче?

Найти ВС и площадь АВС.

Задачу дорешать можете? Почему?

Не хватает знаний.

(Задачи подобраны таким образом, чтобы ситуация успеха сменилась проблемой. Как найти стороны прямоугольного треугольника? Заострить внимание на смысле слова “зависимость”)

III. Изучение нового материала

Какую поставим перед собой задачу?

Как найти гипотенузу и катет в прямоугольном треугольнике?

Итак, какая существует зависимость между катетами и гипотенузой в прямоугольном треугольнике?

Я вам предлагаю прямоугольный треугольник со сторонами 3, 4 и 5. Определите зависимость между этими сторонами. Догадаетесь или нет?

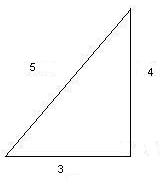
Рисунок 10

5² = 4² + 3²

А выполняется ли эта зависимость в этом треугольнике?

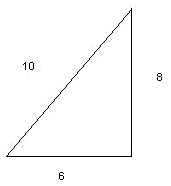
Рисунок 11

Да, 10² = 6² + 8²

Давайте прочитаем на языке геометрии, что же за зависимость получилась?

Квадрат гипотенузы равен сумме квадратов катетов.

Таких чисел очень много! И так, какую гипотезу мы выдвигаем?

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Можно этой зависимостью пользоваться при решении задач?

Нет! Мы же не доказали!

А верно ли что для любого прямоугольного треугольника?

Не знаем! Надо доказать это!

Давайте сформулируем эту теорему.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Историческая справка.

Впервые эту теорему доказал древнегреческий ученый Пифагор, живший в VI веке до н. э. Поэтому она носит имя Пифагора.

Работа в тетрадях.

Запишите тему урока “Теорема Пифагора”. Кто сможет сформулировать эту теорему?

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

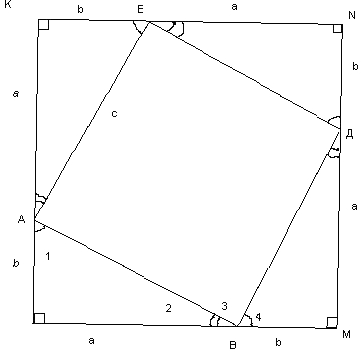
Рисунок 12

Дано:

АВС

С = 90°

а, в – катеты

с – гипотенуза

Доказать:

с² = а² + в²

Доказательство

Доказывается по аналогии с теоремой о площади прямоугольника. Достроим до квадрата со стороной а + в.

Что можно найти?

Площадь.

Чему равна площадь квадрата CMNK?

Квадрату его стороны, т. е. S = (а + в)² = а² + 2ав + в². (1)

Давайте соединим концы этих отрезков. Обозначим буквами эти точки АВДЕ. На чертеже подпишем и обозначим стороны получившихся фигур. Образовавшиеся треугольники равны?

По двум катетам!

Обозначим углы этих треугольников. Против равных сторон лежат равные углы. Что произошло с квадратом?

Он разделен на фигуры – 4 треугольника и четырехугольник ДВЕА.

Как еще можно найти площадь квадрата?

По второму свойству S_CMNK = 4 * S_АВС + S_ВДЕА, S_АВС = ав.

Как найти S_ВДЕА? Что надо знать? Какой это четырехугольник?

Стороны равны с.

Квадрат? Мы же не знаем, что нельзя верить глазам своим, если речь идет о геометрии. И определение вида этого четырехугольника на глаз не годится. Значит надо доказать! Давайте определим угол В!

1 + 2 = 90° (по свойству острых углов);

1 + 4 + 3 = 180° (составляет развернутый угол);

2 = 4 (из равенства треугольников);

(1 + 2) + 3 = 180° ;

90° + 3 = 180° ;

3 = 180° – 90° ;

3 = 90° .

Аналогично можно доказать что остальные углы равны 90° . Какой можно сделать вывод?

Четырехугольник ВДЕА – квадрат со стороной а.

Чему равна площадь ВДЕА?

Квадрату его стороны! S_ВДЕА = с².

Вернемся к площади квадрата CMNK.

S_CMNK = 4 * ав + с²= 2ав + с². (2)

Посмотрите на равенства (1) и (2). Что вы видите?

Левые части равенств равны.

Вывод!

Правые тоже равны; т. е. а² + 2ав + в² = 2ав + с², а² + в² = с² или с² = а² + в².

И так, мы взяли произвольный прямоугольный треугольник со сторонами а, в, с и доказали, что?

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Мы получили формулу, которая выражает зависимость между гипотенузой и катетами прямоугольного треугольника. Значит по этой формуле можно найти квадрат гипотенузы: с²= а² + в².Что для этого нужно знать?

Катеты.

Как найти квадрат катета?

а²= с² - в^2., в² = с² - а².

При решении задач чаще используются прописные буквы, обозначающие вершины. Запишите теорему Пифагора для этих треугольников.

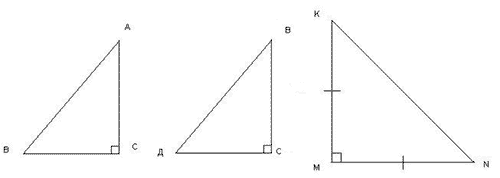
Рисунок 13

АВ²= АС² + ВС², ВД² = ВС² + ДС², NK² = KM² + MN².

IV. Закрепление

Для чего нужна теорема Пифагора? Что можно найти с помощью этой теоремы? Давайте дорешаем задачи .

По теореме Пифагора АВ²= АС² + ВС²; АВ² = 6² + 8²; АВ² = 36 + 64; АВ² = 100; АВ = 10.

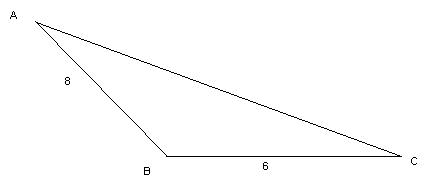
Рисунок 14

По теореме Пифагора

АВ²= АС² + ВС²;

5² = 4² + ВС²;

16 + ВС²= 25;

ВС²= 25 - 16; ВС² = 3 (см.).

S_АВС = * 4 * 3 = 2 * 3 = 6 (см².).

Будет ли верна теорема для АВС ? Найдите сторону АС?

Запомните! Только в прямоугольном треугольнике можно пользоваться этой формулой для нахождения неизвестной стороны.

V. Подведение итогов урока

Учитель еще раз обращает внимание на основные моменты урока, отмечает самых активных учеников, выставляет оценки.

На переносной доске (справа от доски) шутливая формулировка теоремы.

Если дан нам треугольник
Ипритом с прямым углом;
То квадрат гипотенузы
Мы всегда легко найдем:

Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путем
К результату мы придем.

VI. Задание на дом